What is probability?, Slides of Quantitative Techniques

Download What is probability? and more Slides Quantitative Techniques in PDF only on Docsity!

Basic

Probability

Concepts

Dr Mona Hassan Ahmed Hassan Prof of Biostatistics High Institute of Public Health Alexandria, Egypt

Introduction

People use the term probability

many times each day. For example,

physician says that a patient has a

50-50 chance of surviving a certain

operation. Another physician may

say that she is 95% certain that a

patient has a particular disease

Definition

Experiment ==> any planned process

of data collection. It consists of a

number of trials (replications) under

the same condition.

Male, Female Sample space: collection of unique, non-overlapping possible outcomes of a random circumstance. Simple event: one outcome in the sample space; a possible outcome of a random circumstance. Event: a collection of one or more simple events in the sample space; often written as A, B, C, and so on

Definition

Views of Probability: 1-Subjective: It is an estimate that reflects a person’s opinion, or best guess about whether an outcome will occur. Important in medicine  form the basis of a physician’s opinion (based on information gained in the history and physical examination) about whether a patient has a specific disease. Such estimate can be changed with the results of diagnostic procedures.

2- Objective Classical

• It is well known that the probability of flipping a fair coin and getting a “tail” is 0.50.
• If^ a^ coin^ is^ flipped^10 times,^ is^ there^ a guarantee, that exactly 5 tails will be observed
• If the coin is flipped 100 times? With 1000 flips?
• As^ the^ number^ of^ flips^ becomes^ larger,^ the proportion of coin flips that result in tails approaches 0.

2- Objective

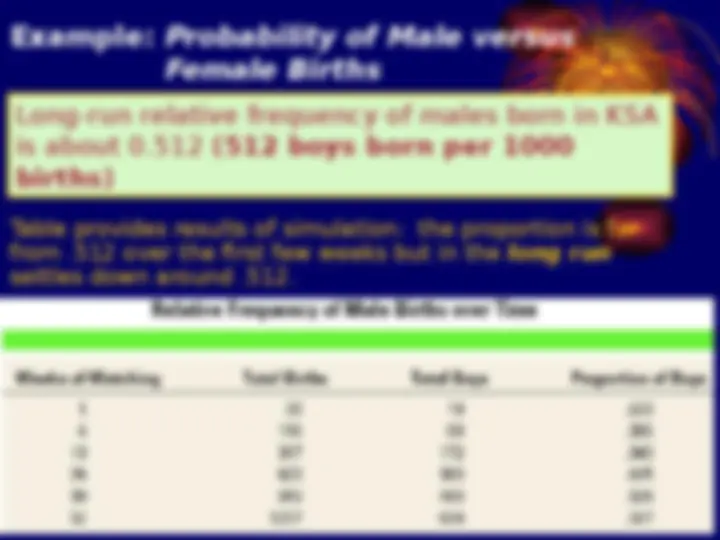
Relative frequency Assuming that an experiment can be repeated many times and assuming that there are one or more outcomes that can result from each repetition. Then, the probability of a given outcome is the number of times that outcome occurs divided by the total number of repetitions.

Problem 1. Blood Group Males Females Total O A B AB 20 17 8 5 20 18 7 5 40 35 15 10 Total 50 50 100

Marginal probabilities Named so because they appear on the “margins” of a probability table. It is probability of single outcome

Example: In problem 1, P(Male), P(Blood

group A)

P(Male) = number of males/total

number of subjects

Conditional probabilities It is the probability of an event on condition that certain criteria is satisfied Example: If a subject was selected randomly and found to be female what is the probability that she has a blood group O Here the total possible outcomes constitute a subset (females) of the total number of subjects. This probability is termed probability of O given F P(O\F) = 20/ = 0.

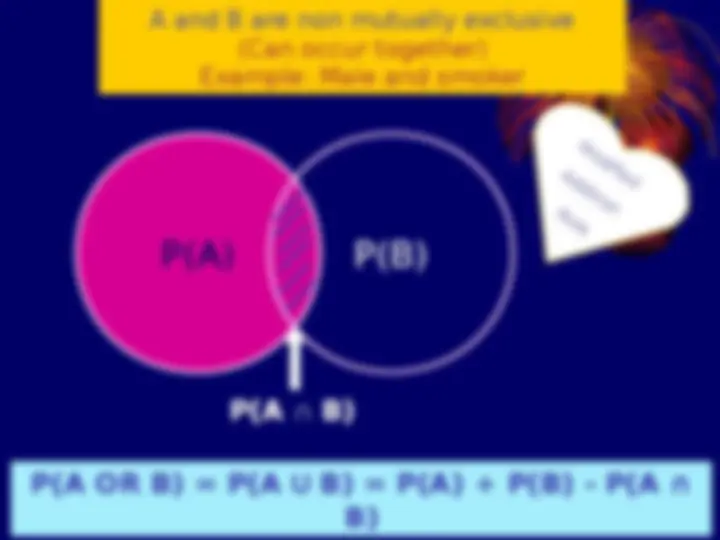
Properties The probability ranges between 0 and 1 If an outcome cannot occur, its probability is 0 If an outcome is sure, it has a probability of 1 The sum of probabilities of mutually exclusive outcomes is equal to 1 P(M) + P(F) = 1

Rules of probability 1- Multiplication rule

Independence and multiplication rule

P(A and B) = P(A) P(B)

Example:

The joint probability of being male and having blood type O To know that two events are independent compute the marginal and conditional probabilities of one of them if they are equal the two events are independent. If not equal the two events are dependent P(O) = 40/100 = 0. P(O\M) = 20/50 = 0. Then the two events are independent P(O∩M) = P(O)P(M) = (40/100)(50/100) = 0.

Rules of probability 1- Multiplication rule

Dependence and

the modified multiplication rule

P(A and B) = P(A) P(B\A)