Download Weighted Graphs and Distances - Computational Concepts in Biological Sciences - Lecture Note and more Lecture notes Computer Science in PDF only on Docsity!
So far, we assume that the distance between two
vertices is the number of edges.
We can also presume that there is a distance assigned to
each edge.
In this case, we have to change our algorithms to match.
Weighted graphs and distances
Monday, November 22, 2010 12:22 PM
Docsity.com
Definition: A weighted graph G=(V,E) is any graph where
there is a weight function w: E→ R that assigns a real
number to each edge.
Example: distances between cities.
w('boston','woburn')=10 miles
Example: time to get between places
w('boston', 'woburn')=15 minutes
Weighted graphs
Sunday, November 21, 2010 10:40 AM
Docsity.com
You may have seen a table of distances between cities in
a road atlas.
Example: road atlas
Wednesday, December 01, 2010 3:06 PM
Docsity.com
The shortest path problem: given a weighted graph and
two vertices, find the shortest path between the vertices.
The shortest path problem
Wednesday, December 01, 2010 10:11 AM
Docsity.com
When there are many solutions to a problem, we need a
way to judge which one is "best".
An objective function is a mapping from problem
solutions to a numeric score, e.g., a distance.
An optimization problem is to maximize or minimize
some objective function, e.g., distance along a path.
An optimization problem is convex if a local optimum is
a global optimum.
Convexity
Monday, November 22, 2010 12:02 PM
Docsity.com
In our shortest-path algorithm, we start from the source
node, and know that at any time, the labeled distances to
the source node are minimal.
Thus the new distances, calculated by traversing new
edges, are going to be minimal as well.
But we need to adapt this algorithm for weights (our
solution only works if every weight is 1).
The shortest-path problem is convex
Wednesday, December 01, 2010 10:13 AM
Docsity.com
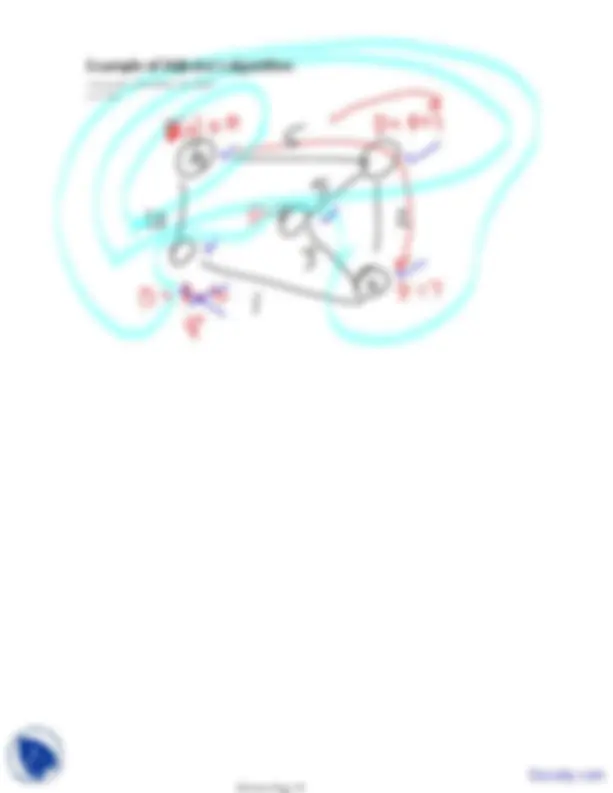
Example of Dijkstra's algorithm
Wednesday, December 01, 2010 3:17 PM
Docsity.com
Once you have a minimum distance to a, it stays
minimum => you can find the shortest path by
considering only n vertices. => runtime is O(n+e),
n=|V|, e=|E|.
Some problems are convex:
Example: the traveling salesman problem.
"Find a minimum-length cycle that passes through all
vertices and returns to the source, without repeating
an edge."
Some problems are not convex:
The bigger picture
Wednesday, December 01, 2010 3:24 PM
Docsity.com
It is extremely difficult to implement this using concrete structures; it's
too easy to forget what is what.
So we'll use abstraction.
If $foo is a reference blessed into a package Bar,
then $foo->function(@stuff)
means &Bar::function($foo,@stuff)
The basic rule of abstraction:
In other words, the blessing determines which function is called.
my $s = new Stack;
my $q = new Queue;
$s1 = $s->size; # calls &Stack::size($s)
$s2 = $q->size; # calls &Queue::size($q);
Example:
Implementing Dijkstra's algorithm
Wednesday, December 01, 2010 10:39 AM
Docsity.com
my $map = new Map;
$map->set($key,$value);
my $storedVal = $map->get($key);
my @keys = $map->keys;
Map:
Step 1: classes we will use:
Wednesday, December 01, 2010 10:43 AM
Docsity.com
my $graph = new Graph;
$graph->addEdges('boston', 'newyork', 100);
my $distances = new Map;
my $usedDists = new Map;
$distances->set($source,0);
$distances->get($vertex) is defined if $vertex hasn't
been visited. In this case, the distance need not be minimal.
$usedDists->get($vertex) is defined if $vertex has
been visited. In this case, the distance is minimal.
Meaning of our representation:
Step 3: represent algorithm concepts
Wednesday, December 01, 2010 10:50 AM
Docsity.com
find minimum-distance vertex that hasn't been visited yet
my $minVertex = undef; my $minDistance = undef; foreach my $vertex ($distances->keys) { $minVertex = $vertex; $minDistance = $distances->get($vertex); } if (! defined $minDistance || $distances->get($vertex)<$minDistance) { }
for each neighbor of the current minimum-distance unvisited vertex,
foreach my $vertex ($graph->neighbors($minVertex)) { next if defined $distances->get($vertex); # skip if distance is known next if defined $usedDists->get($vertex);
shortest distance to new vertex is through $minVertex
$distances->set( $vertex, $minDistance+$graph->edgeLabel($minVertex, $vertex)) if! defined $distances->get($vertex) || ($minDistance+$graph->edgeLabel($minVertex, $vertex)) <$distances->get($vertex);
mark $minVertex visited and its distance as minimal
$usedDists->set($minVertex,$distances->get($minVertex)); $distances->remove($minVertex);
Pasted from http://www.cs.tufts.edu/comp/14/examples/Distance/WG_dijkstra_dist.perl
Step 4: do one step of the algorithm
Wednesday, December 01, 2010 10:54 AM
Docsity.com