
































Study with the several resources on Docsity

Earn points by helping other students or get them with a premium plan


Prepare for your exams
Study with the several resources on Docsity

Earn points to download
Earn points by helping other students or get them with a premium plan
Community
Ask the community for help and clear up your study doubts
Discover the best universities in your country according to Docsity users
Free resources
Download our free guides on studying techniques, anxiety management strategies, and thesis advice from Docsity tutors
various kinds of the association rule
Typology: Lecture notes
1 / 40

This page cannot be seen from the preview
Don't miss anything!

































(^) Association rule mining Algorithms for scalable mining of (single-dimensional Boolean) association rules in transactional databases (^) Mining various kinds of association/correlation rules Constraint-based association mining Sequential pattern mining Applications/extensions of frequent pattern mining Summary
Association rule mining: A transaction T in a database supports an itemset S if S is contained in T An itemset that has support above a certain threshold, called minimum support, is termed large ( frequent ) itemset Frequent pattern: pattern (set of items, sequence, etc.) that occurs frequently in a database Finding frequent patterns, associations, correlations, or causal structures among sets of items or objects in transaction databases, relational databases, and other information repositories.
Association rule mining is a two-step process: Find all frequent itemsets Generate strong association rules from the frequent itemsets For every frequent itemset L , find all non-empty subsets of L. For every such subset A , output a rule of the form “ A ( L - A )” if the ratio of support( L ) to support( A ) is at least minimum confidence The overall performance of mining association rules is determined by the first step
For rule A C : support = support({ A }{ C }) = 50% confidence = support({ A }{ C })/support({ A }) = 66.6%
Transaction-id Items bought 10 A, B, C 20 A, C 30 A, D 40 B, E, F Frequent pattern Support {A} 75% {B} 50% {C} 50% {A, C} 50%
The name, Apriori , is based on the fact that the algorithm uses prior knowledge of frequent itemset properties Apriori employs an iterative approach known as a level- wise search, where k-itemsets are used to explore (k+1)-itemsets The first pass determines the frequent 1-itemsets denoted L 1 A subsequence pass k consists of two phases (^) First, the frequent itemsets L k-1 are used to generate the candidate itemsets Ck (^) Next, the database is scanned and the support of candidates in Ck is counted (^) The frequent itemsets L k are determined
(^) How to generate candidates? (^) Step 1: self-joining L k (^) Step 2: pruning (^) How to count supports of candidates? (^) Example of candidate-generation (^) L 3 = { abc, abd, acd, ace, bcd } (^) Self-joining: L 3 *L 3 (^) abcd from abc and abd acde from acd and ace Pruning: (^) acde is removed because ade is not in L 3 (^) C 4 ={ abcd }
insert into Ck select p.item 1 , p.item 2 , …, p.itemk-1, q.itemk- from Lk-1 p, Lk-1 q where p.item 1 =q.item 1 , …, p.itemk-2=q.itemk-2, p.itemk-1 < q.itemk-
forall itemsets c in Ck do forall (k-1)-subsets s of c do
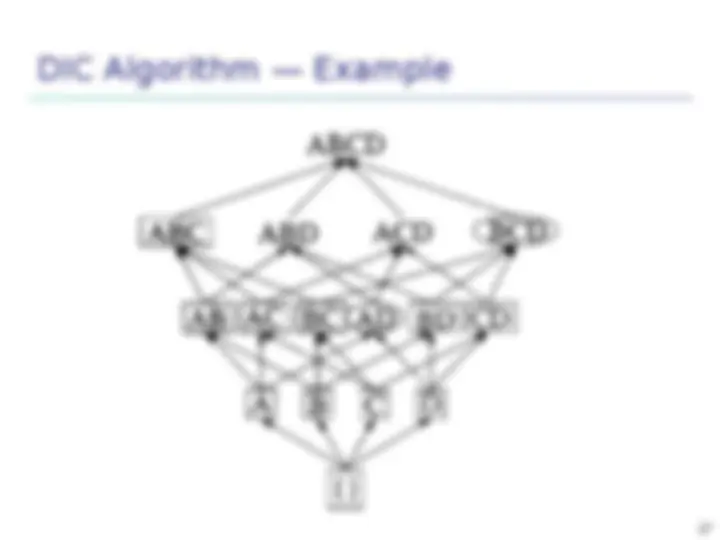
The intuition behind DIC is that it works like a train running over the data with stops at intervals M transactions apart. If we consider Apriori in this metaphor, all itemsets must get on at the start of a pass and get off at the end. The 1-itemsets take the fist pass, the 2-itemsets take the second pass, and so on. In DIC, we have the added flexibility of allowing itemsets to get on at any stop as long as they get off at the same stop the next time the train goes around. We can start counting an itemset as soon as we suspect it may be necessary to count it instead of waiting until the end of the previous pass.
(^) For example, if we are mining 40,000 transactions and M = 10,000, we will count all the l-itemsets in the first 40,000 transactions we will read. However, we will begin counting 2-itemsets after the first 10,000 transactions have been read. We will begin counting 3-itemsets after 20,000 transactions. (^) We assume there are no 4-itemsets we need to count. Once we get to the end of the file, we will stop counting the l-itemsets and go back to the start of the file to count the 2 and 3-itemsets. After the first 10, transactions, we will finish counting the 2-itemsets and after 20,000 transactions, we will finish counting the 3- itemsets. In total, we have made 1.5 passes over the data instead of the 3 passes a level-wise algorithm would make.