Partial preview of the text
Download Union-Find Problem - Algorithms and Applications in Java - Lecture Slides and more Slides Computer Science in PDF only on Docsity!
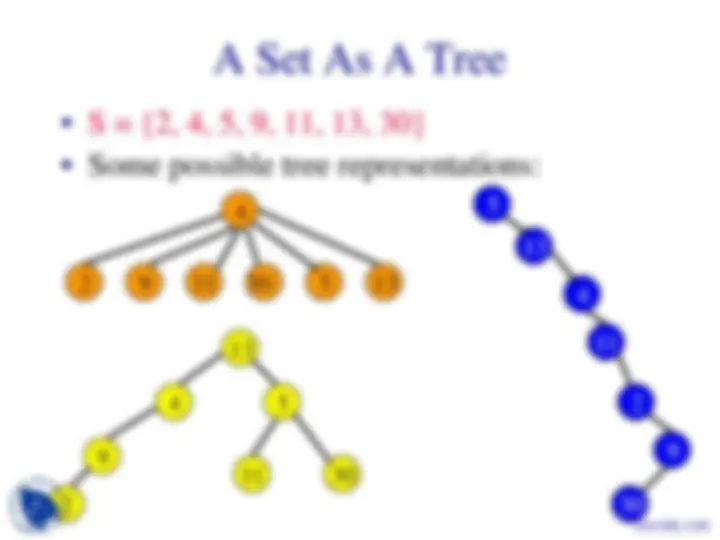
Union-Find Problem
• Given a set {1, 2, …, n} of n elements.
• Initially each element is in a different set.
{1}, {2}, …, {n}
• An intermixed sequence of union and find
operations is performed.
• A union operation combines two sets into one.
Each of the n elements is in exactly one set at any
time.
• A find operation identifies the set that contains
a particular element.
Using Arrays And Chains
• See Section 7.7 for applications as well as for
solutions that use arrays and chains.
• Best time complexity obtained in Section 7.7 is
O(n + u log u + f), where u and f are,
respectively, the number of union and find
operations that are done.
• Using a tree (not a binary tree) to represent a
set, the time complexity becomes almost
O(n + f) (assuming at least n/2 union
operations).
Result Of A Find Operation
• find(i) is to identify the set that contains element i.
• In most applications of the union-find problem, the
user does not provide set identifiers.
• The requirement is that find(i) and find(j) return
the same value iff elements i and j are in the same
set.
find(i) will return the element that is in the tree root.
Strategy For find(i)
• Start at the node that represents element i and
climb up the tree until the root is reached.
• Return the element in the root.
• To climb the tree, each node must have a parent
pointer.
Possible Node Structure
• Use nodes that have two fields: element and
parent.
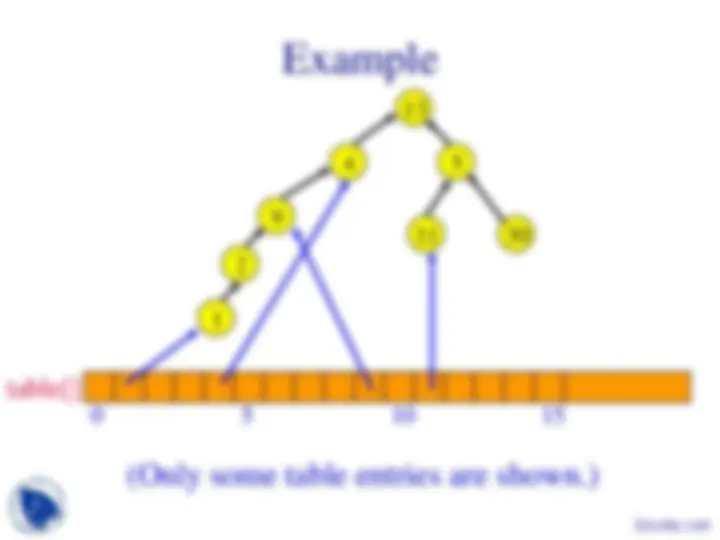
Use an array table[] such that table[i] is a
pointer to the node whose element is i.
To do a find(i) operation, start at the node given
by table[i] and follow parent fields until a node
whose parent field is null is reached.
Return element in this root node.
Example
table[]
(Only some table entries are shown.)
Union Operation
• union(i,j)
i and j are the roots of two different trees, i != j.
• To unite the trees, make one tree a subtree
of the other.
parent[j] = i
Union Example
• union(7,13)
The Union Method
public void union(int rootA, int rootB)
{parent[rootB] = rootA;}
Time Complexity Of union()
• O(1)
u Unions and f Find Operations
• O(u + uf) = O(uf)
• Time to initialize parent[i] = 0 for all i is
O(n).
• Total time is O(n + uf).
• Worse than solution of Section 7.7!
• Back to the drawing board.
Smart Union Strategies
• union(7,13)
• Which tree should become a subtree of the other?
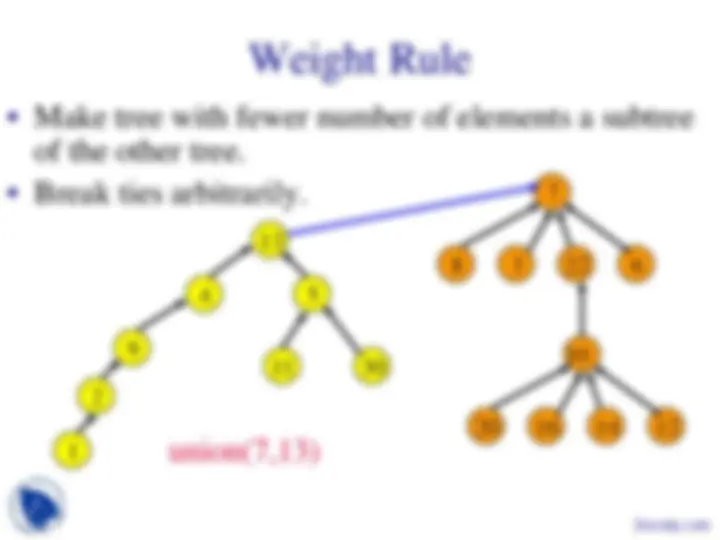
Weight Rule
• Make tree with fewer number of elements a subtree
of the other tree.
• Break ties arbitrarily.
union(7,13)
Implementation
• Root of each tree must record either its
height or the number of elements in the tree.
• When a union is done using the height rule,
the height increases only when two trees of
equal height are united.
• When the weight rule is used, the weight of
the new tree is the sum of the weights of the
trees that are united.