





































Study with the several resources on Docsity

Earn points by helping other students or get them with a premium plan


Prepare for your exams
Study with the several resources on Docsity

Earn points to download
Earn points by helping other students or get them with a premium plan
Community
Ask the community for help and clear up your study doubts
Discover the best universities in your country according to Docsity users
Free resources
Download our free guides on studying techniques, anxiety management strategies, and thesis advice from Docsity tutors
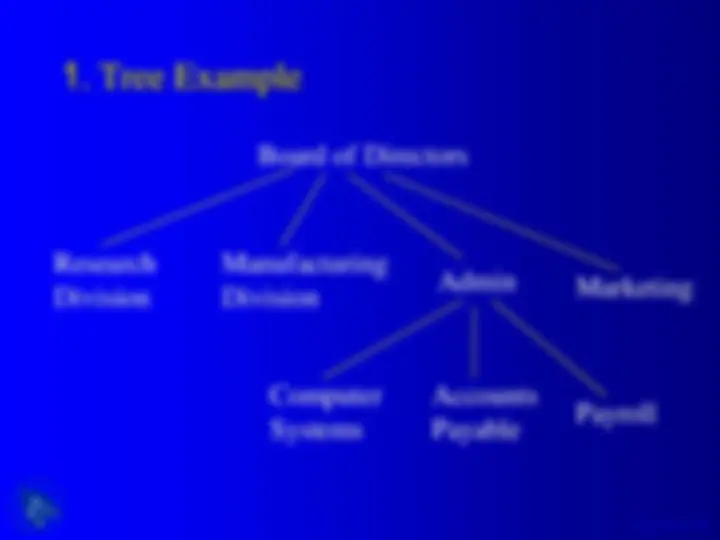
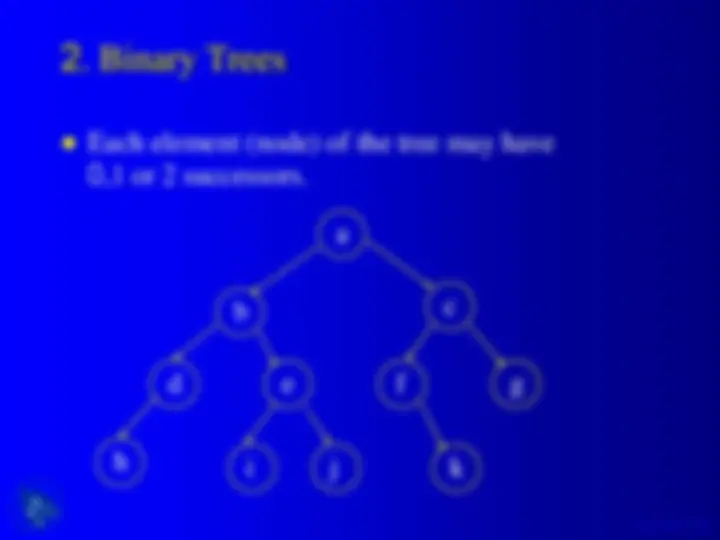
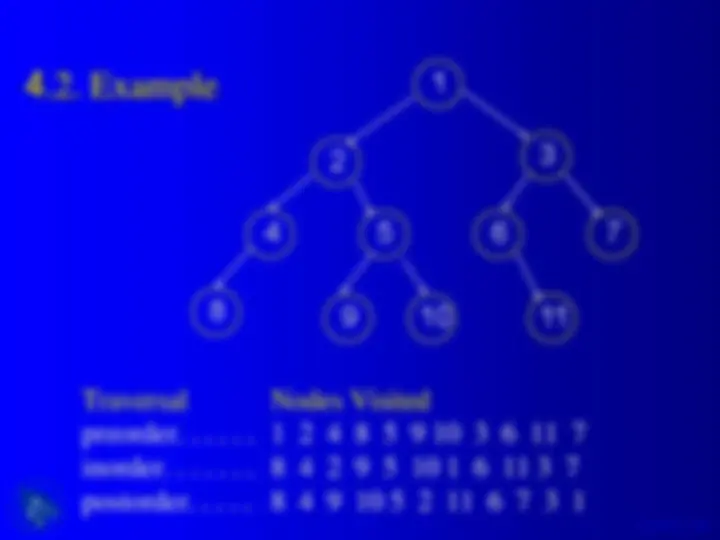
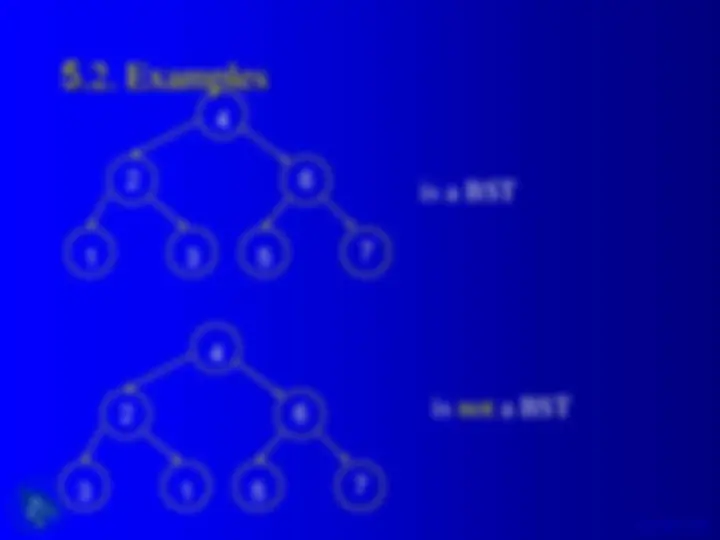
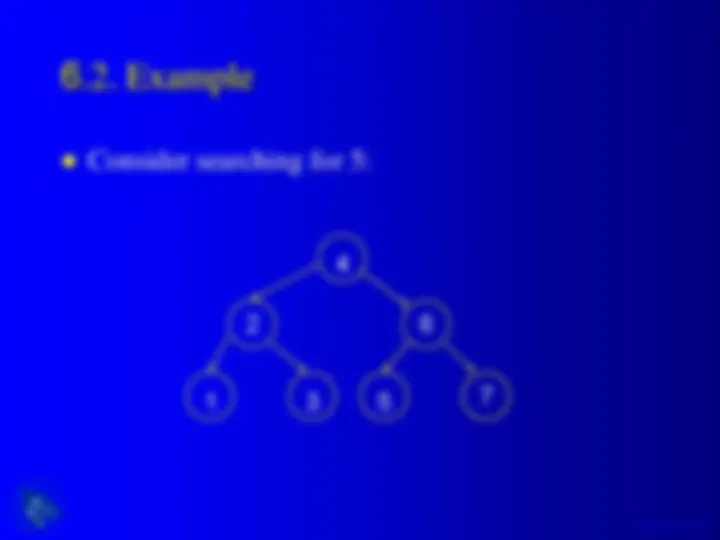
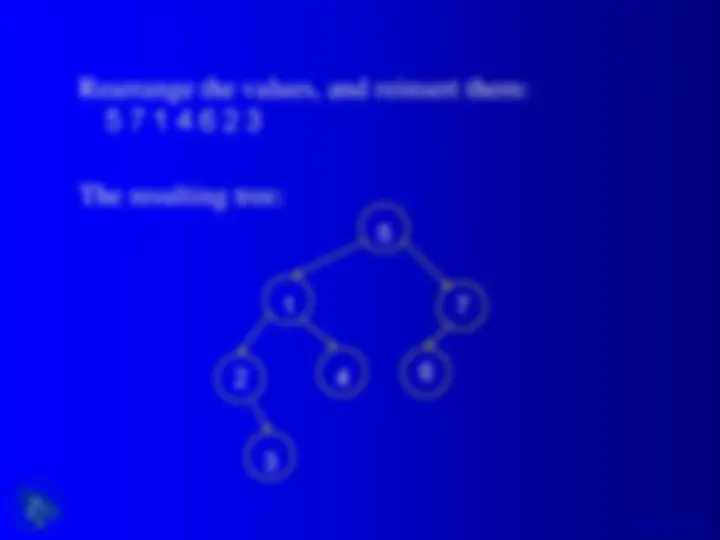
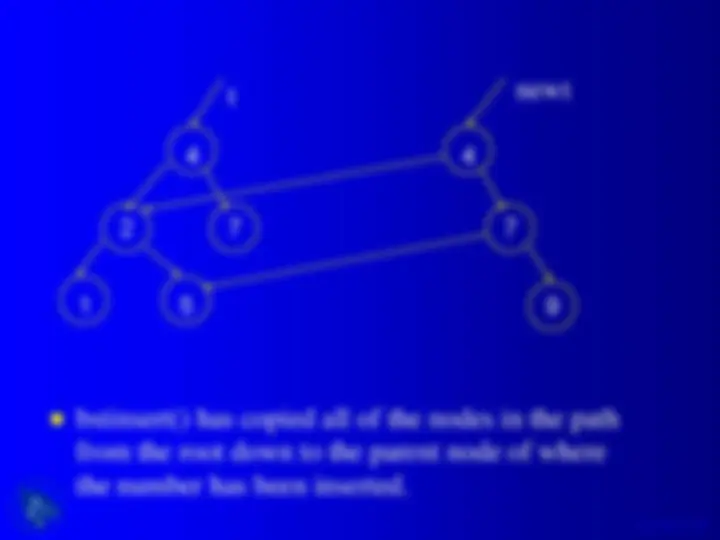
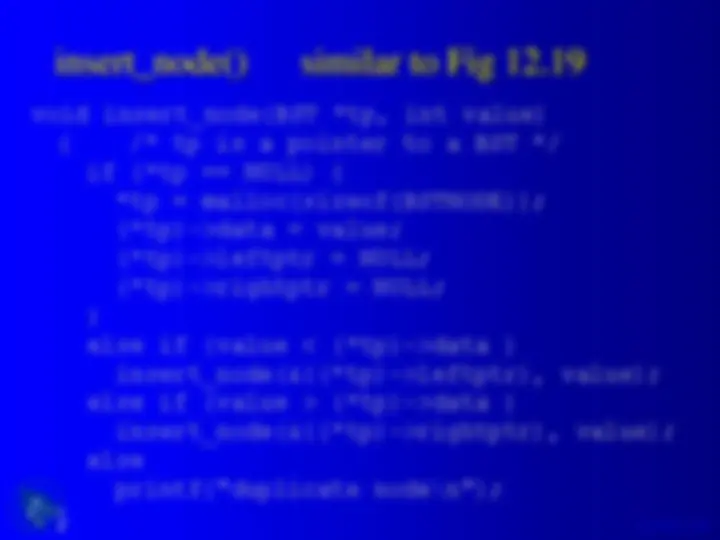
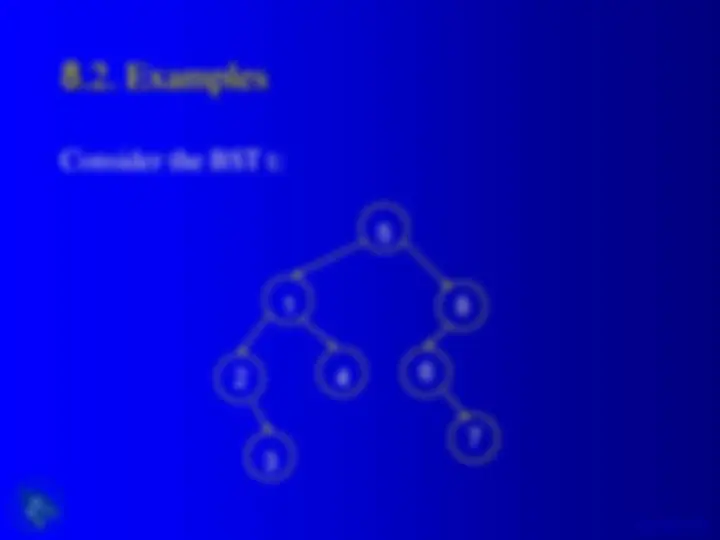
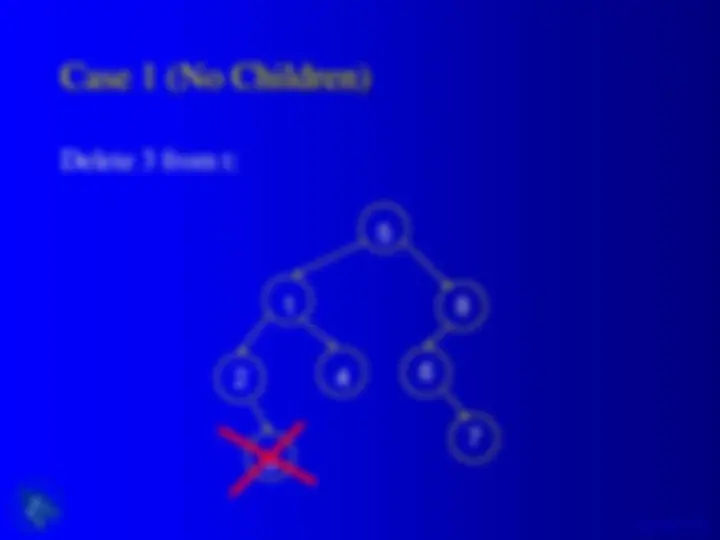
An overview of binary trees and binary search trees, their jargon, shape, and some functions in c language. It includes examples of binary tree adt operations, binary tree type, size and height of a binary tree, tree traversal methods (preorder, inorder, postorder), and searching, insertion, and deletion in a binary search tree.
Typology: Slides
1 / 58

This page cannot be seen from the preview
Don't miss anything!



















































TREE t;
t = NULL;
t t^ NULL t 2 N N
t 2 4 7
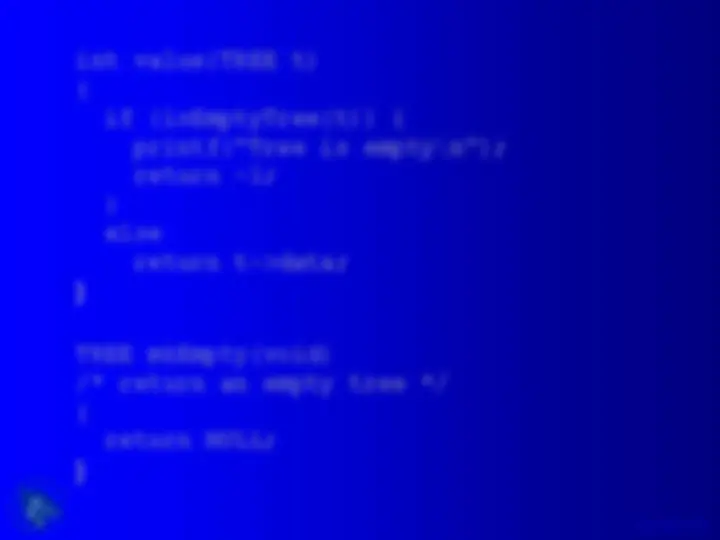
int value(TREE t) { if (isEmptyTree(t)) { printf(“Tree is empty\n”); return -1; } else return t->data; } TREE mkEmpty(void) /* return an empty tree */ { return NULL; }
TREE mkTree(int x, TREE leftT, TREE rightT) /* make a new tree from a data value x and two existing trees */ { TREE temp; temp = malloc(sizeof(TREENODE)); temp->data = x; temp->leftptr = leftT; temp->rightptr = rightT; return temp; }
int size(TREE t) { if (isEmptyTree(t)) return 0; else return (1 + size(lsTree(t))
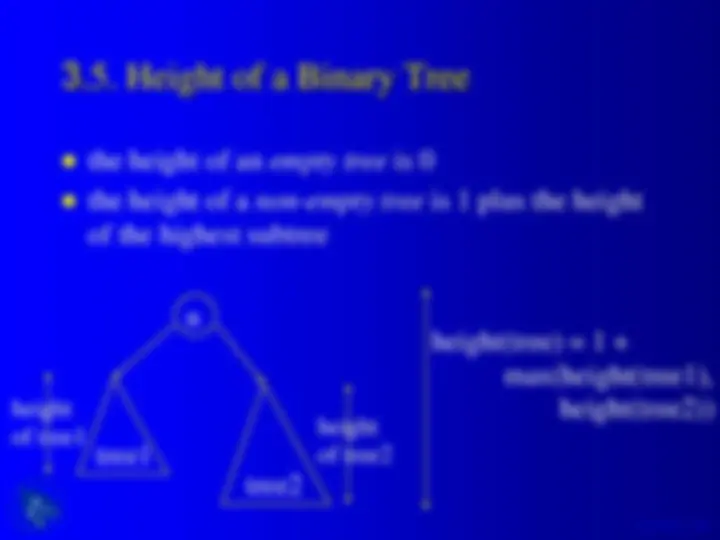
height of tree height of tree
int height(TREE t) { if(isEmptyTree(t)) return 0; else return (1 + max(height(lsTree(t)), height(rsTree(t)))); }