Study with the several resources on Docsity
Earn points by helping other students or get them with a premium plan
Prepare for your exams
Study with the several resources on Docsity
Earn points to download
Earn points by helping other students or get them with a premium plan
Community
Ask the community for help and clear up your study doubts
Discover the best universities in your country according to Docsity users
Free resources
Download our free guides on studying techniques, anxiety management strategies, and thesis advice from Docsity tutors
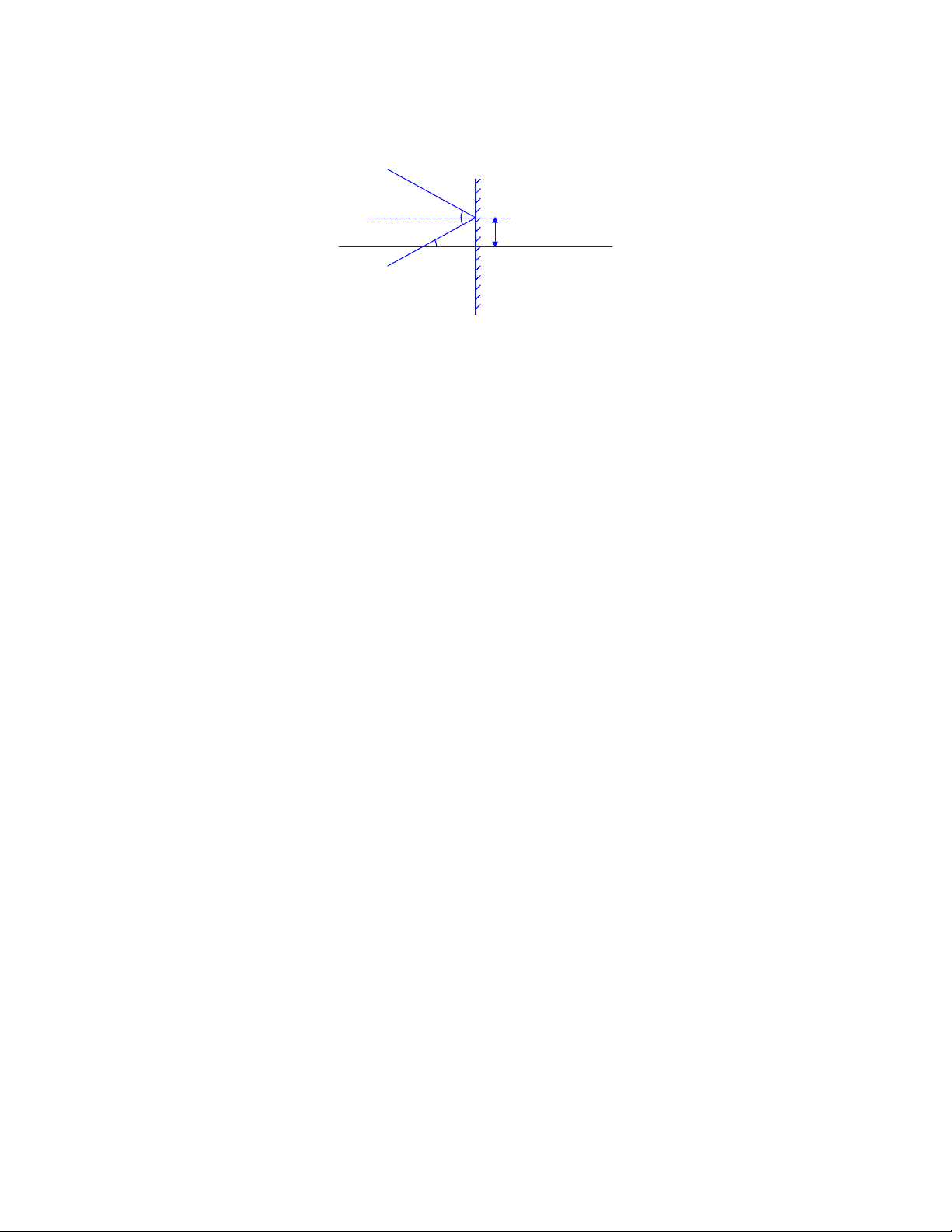
The geometry and calculation steps to derive the transform matrix for a ray incident on a flat mirror perpendicular to the optic axis. The mirror reverses the direction of propagation while maintaining the angle of incidence and deviation from the optic axis. A diagram showing the ray's geometry and the derived transform matrix.
Typology: Exams
1 / 1
This page cannot be seen from the preview
Don't miss anything!
α^ y^0 = y^1 0
α 0
α 1
The ray strikes the mirror and reflects at the same angle. The deviation from the optic axis is not changed by the mirror, but the direction of propagation is reversed. So we have:
y 1 = y 0
α 1 = −α 0 ( y 1 α 1
y 0 α 0
