Thermal Properties of Materials - Material Science for Engineers - Lecture Slides, Slides of Material Engineering

Download Thermal Properties of Materials - Material Science for Engineers - Lecture Slides and more Slides Material Engineering in PDF only on Docsity!

The Science and Engineering of

Materials, 4

th

ed

Chapter 21 – Thermal Properties of

Materials

Objectives of Chapter 21

• To discuss heat capacity, thermal expansion properties,

and the thermal conductivity of materials.

• Phonon - A packet of elastic waves. It is characterized by its energy, wavelength, or frequency, which transfers energy through a material.
• Specific heat - The energy required to raise the temperature of one gram of a material by one degree.

Section 21.

Heat Capacity and Specific Heat

©2003 Brooks/Cole, a division of Thomson Learning, Inc. Thomson Learning™ is a trademark used herein under license.

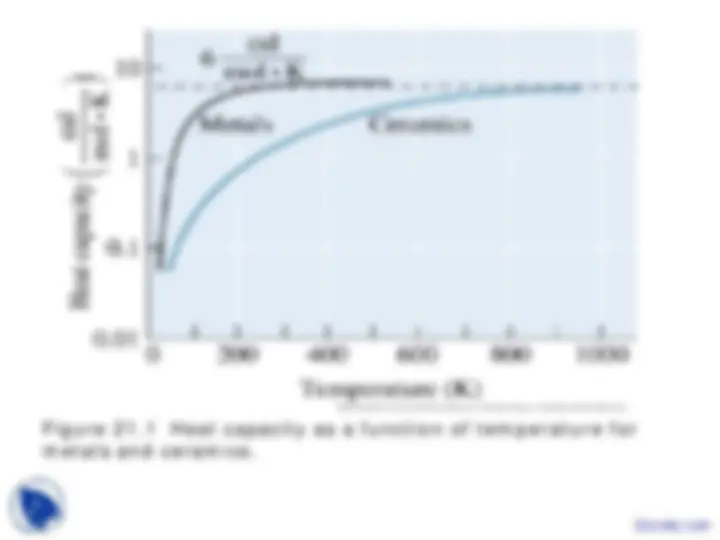
Figure 21.1 Heat capacity as a function of temperature for metals and ceramics.

How much heat must be supplied to 250 g of tungsten to raise its temperature from 25 o^ C to 650 o^ C?

Example 21.1 SOLUTION

Example 21. Specific Heat of Tungsten

If no losses occur, 5000 cal (or 20,920 J) must be supplied to the tungsten.

Suppose the temperature of 50 g of niobium increases 75o^ C when heated for a period. Estimate the specific heat and determine the heat in calories required.

Example 21.2 SOLUTION

The atomic weight of niobium is 92.91 g/mol. We can use Equation 21-3 to estimate the heat required to raise the temperature of one gram by one o^ C:

Example 21. Specific Heat of Niobium

Thus the total heat required is:

©2003 Brooks/Cole, a division of Thomson Learning, Inc. Thomson Learning™ is a trademark used herein under license. Figure 21.3 The relationship between the linear coefficient of thermal expansion and the melting temperature in metals at 25°C. Higher melting point metals tend to expand to a lesser degree.

©2003 Brooks/Cole, a division of Thomson Learning, Inc. Thomson Learning™ is a trademark used herein under license.

Figure 21.4 (a) The linear coefficient of thermal expansion of iron changes abruptly at temperatures where an allotropic transformation occurs. (b) The expansion of Invar is very low due to the magnetic properties of the material at low temperatures.

Example 21.3 SOLUTION

Both silicon and tin are covalently bonded. The strong covalent bonds are more difficult to stretch than the metallic bonds (a deeper trough in the energy-separation curve), so these elements have a lower coefficient. Since germanium also is covalently bonded, its thermal expansion should be less than that predicted by Figure 21.3.

Design the dimensions for a pattern that will be used to produce a rectangular-shaped aluminum casting having dimensions at 25 o^ C of 25 cm × 25 cm × 3 cm.

Example 21.4 SOLUTION

The linear coefficient of thermal expansion for aluminum is 25 × 10 -6^ 1/o^ C. The temperature change from the freezing temperature to 25 o^ C is 660 - 25 = 635 o^ C. The change in any dimension is given by:

Example 21. Design of a Pattern for a Casting Process

For the 25-cm dimensions, l (^) f = 25 cm. We wish to find l 0 :

A ceramic enamel is to be applied to a 1020 steel plate. The ceramic has a fracture strength of 4000 psi, a modulus of elasticity of 15 × 10 6 psi, and a coefficient of thermal expansion of 10 × 10 -6^ 1/o^ C. Design the maximum temperature change that can be allowed without cracking the ceramic.

Example 21. Design of a Protective Coating

Example 21.5 SOLUTION

If only the enamel heated (and the steel remained at a constant temperature), the maximum temperature change would be:

However, the steel also expands. Its coefficient of thermal expansion (Table 21-2) is 12 × 10 -6^ 1/o^ C and its modulus of elasticity is 30 × 10 6 psi. The net coefficient of expansion is

©2003 Brooks/Cole, a division of Thomson Learning, Inc. Thomson Learning™ is a trademark used herein under license.

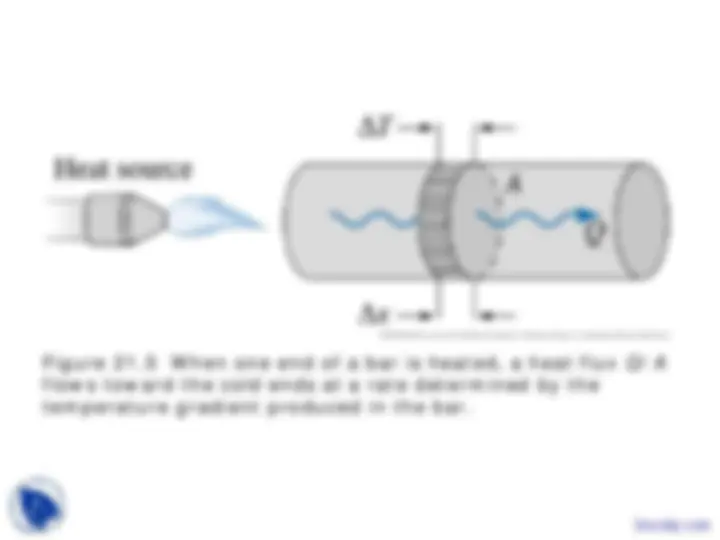
Figure 21.5 When one end of a bar is heated, a heat flux Q/A flows toward the cold ends at a rate determined by the temperature gradient produced in the bar.

©2003 Brooks/Cole, a division of Thomson Learning, Inc. Thomson Learning™ is a trademark used herein under license.

Figure 21.6 The effect of temperature on the thermal conductivity of selected materials. Note the log scale on the y- axis.