











Study with the several resources on Docsity

Earn points by helping other students or get them with a premium plan


Prepare for your exams
Study with the several resources on Docsity

Earn points to download
Earn points by helping other students or get them with a premium plan
Community
Ask the community for help and clear up your study doubts
Discover the best universities in your country according to Docsity users
Free resources
Download our free guides on studying techniques, anxiety management strategies, and thesis advice from Docsity tutors
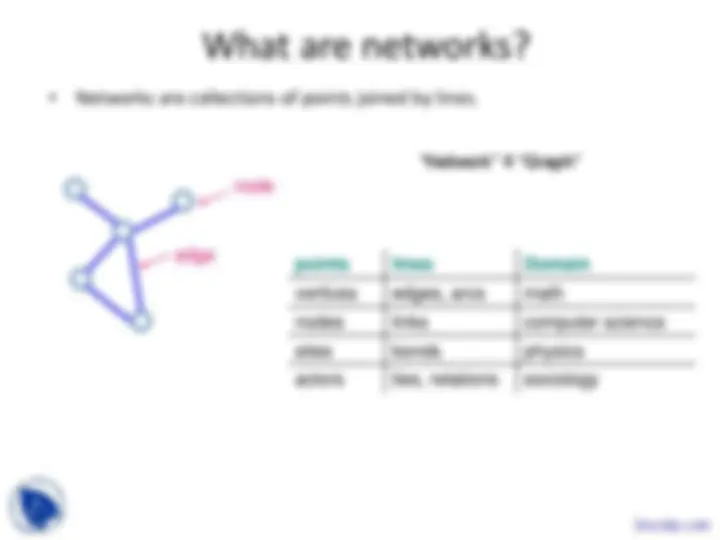
Various aspects of network analysis, including structural and community aspects, dynamics, algorithms, and outlook. It covers questions related to the number of connections, clusters, growth, and propagation of phenomena in networks. The document also discusses the use of graphs, adjacency matrices, and bipartite networks to represent and analyze networks.
Typology: Slides
1 / 22

This page cannot be seen from the preview
Don't miss anything!















particularly strong?
_6. What is the best way to characterize a complex network?
CS 765: Complex Networks
Slides are modified from Networks: Theory and Application by Lada Adamic
Ada
Cora
Louise
Jean
Helen
Martha
Alice
Robin
Marion
Maxine
Lena
Hazel (^) Hilda
Frances Eva
Edna^ Ruth
Adele
Jane
Anna
Mary
Betty
Ella
Ellen
Laura
Irene
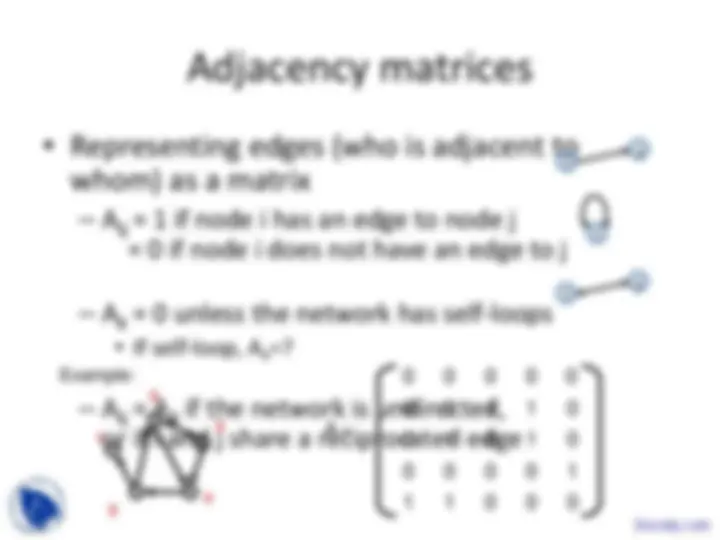
i
j
i
i
j
1
2
3
4
Example:
5
A =
1
2
3
4 5
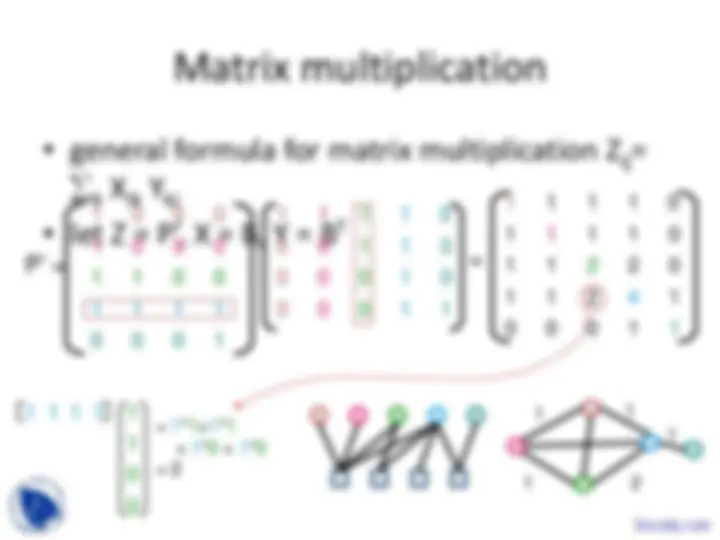
HyperGraphs
Can be transformed to a bipartite network
C D
A B
C D
A B
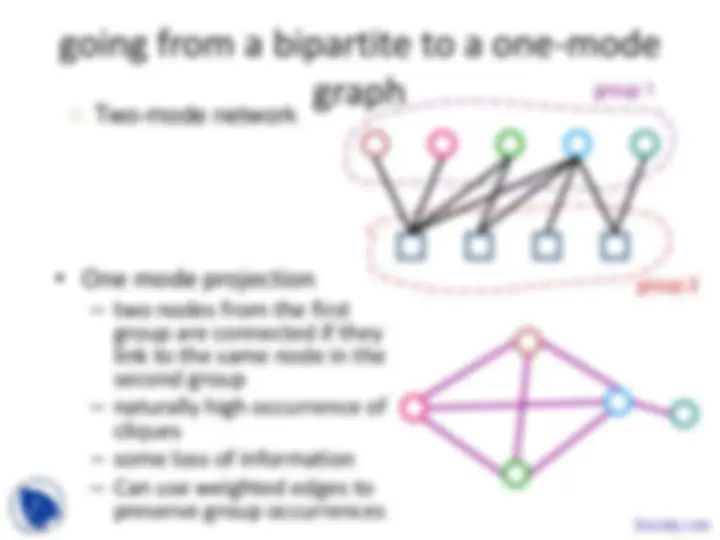
going from a bipartite to a one-mode
graph
group 1
group 2
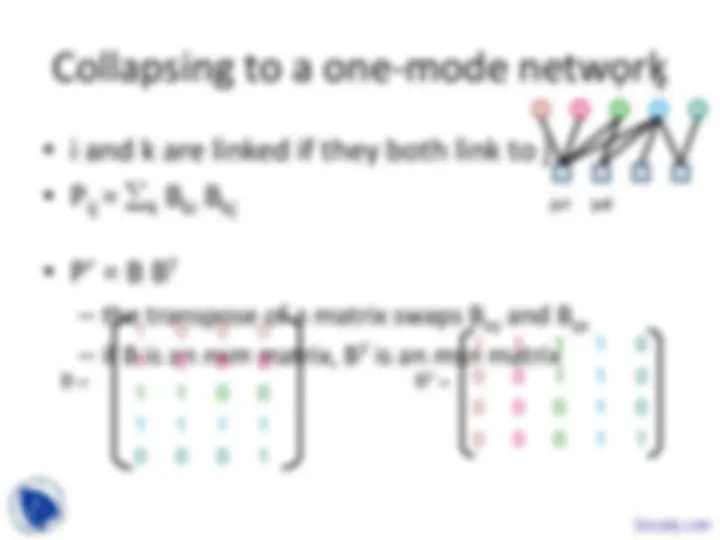
i
j=
k
j=
B = B T^ =