State Minimization
Docsity.com
Prepare for your exams
Study with the several resources on Docsity
Earn points to download
Earn points by helping other students or get them with a premium plan
Guidelines and tips
Prepare for your exams
Study with the several resources on Docsity
Earn points to download
Earn points by helping other students or get them with a premium plan
Community
Ask the community
Ask the community for help and clear up your study doubts
University Rankings
Discover the best universities in your country according to Docsity users
Free resources
Our save-the-student-ebooks!
Download our free guides on studying techniques, anxiety management strategies, and thesis advice from Docsity tutors
State Minimization - Digital System Design - Lecture Slides, Slides of Digital Systems Design
The digital system design, is very helpful series of lecture slides, which made programming an easy task. The major points in these laboratory assignment are:State Minimization, Reduction in States, Distinguishing States, Corresponding Table Cell, Distinguishable Outputs, Final State Reduction Table, Effect of Outputs, Modified Rule, Input Transitions, Moore Fsm Example
Typology: Slides
2012/2013
1 / 20
This page cannot be seen from the preview
Don't miss anything!
Related documents
Partial preview of the text
Download State Minimization - Digital System Design - Lecture Slides and more Slides Digital Systems Design in PDF only on Docsity!
State Minimization
Two Equivalent FSMs
A sensor example: detect and don’t repeat
Two equivalent ways to design the FSM – one has
fewer states than the other
Distinguishing States (2)
Let d(q,x) be the state the follows state q on input x
Example: d(A,1) = B, and d(A,0) = A
Rule 2 : two states A
and A
are distinguishable if
d(A
1
,1) and d(A
2
,1) are distinguishable, or
d(A
1
,0) and d(A
2
,0) are distinguishable
A/
S=
B/
S=
S=
C/
S=
S=
S=
D/
S=
S=
B
C
D
A B C
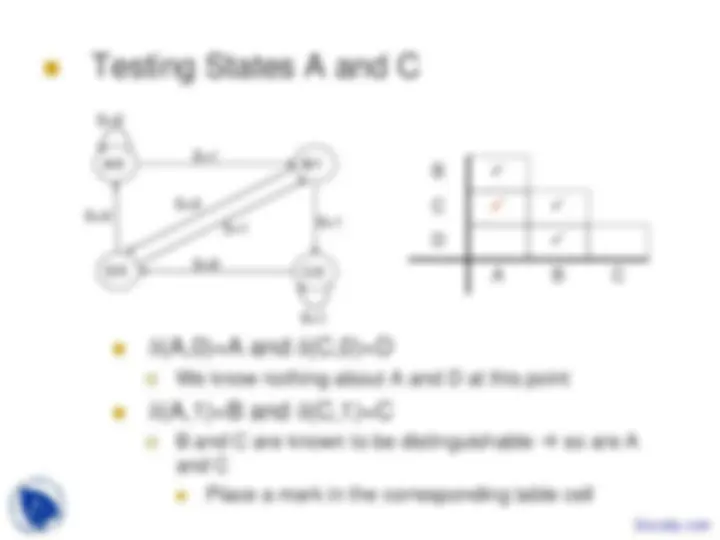
Testing States A and C
d(A,0)=A and d(C,0)=D
We know nothing about A and D at this point
d(A,1)=B and d(C,1)=C
B and C are known to be distinguishable so are A
and C
Place a mark in the corresponding table cell
A/
S=
B/
S=
S=
C/
S=
S=
S=
D/
S=
S=
B
C
D
A B C
Testing States C and D
d(C,0)=D and d(D,0)=A
Looks promising since D and A are the same ….
d(C,1)=C and d(D,1)=B
B and C are known to be distinguishable so are C
and D
Place a mark in the corresponding table cell
A/
S=
B/
S=
S=
C/
S=
S=
S=
D/
S=
S=
B
C
D
A B C
Resulting FSM
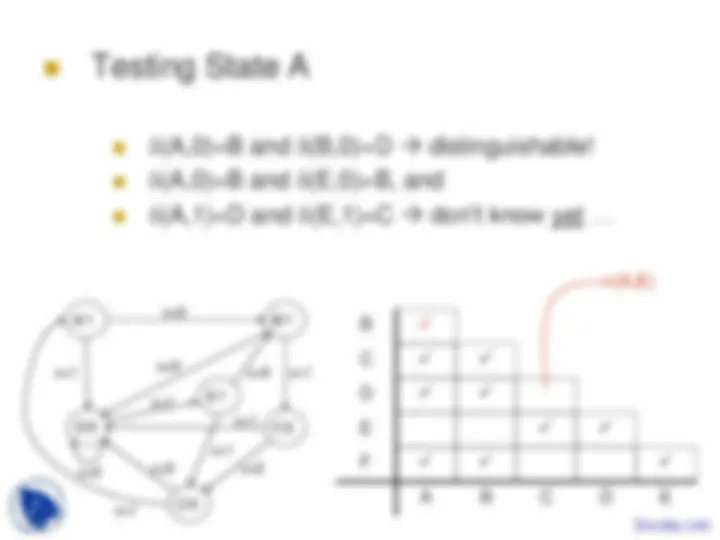
Testing State A
d(A,0)=B and d(B,0)=D distinguishable!
d(A,0)=B and d(E,0)=B, and
d(A,1)=D and d(E,1)=C don’t know yet …
B
C
D
E
F
A B C D E
(A,E)
x=
A/1 B/
x=
D/0 F/
x=
x=
x=
x=
C/
x=0 x=
x=
E/
x=
x=
x=
Testing State B
d(B,0)=D and d(E,0)=B distinguishable!
B
C
D
E
F
A B C D E
(A,E)
x=
A/1 B/
x=
D/0 F/
x=
x=
x=
x=
C/
x=0 x=
x=
E/
x=
x=
x=
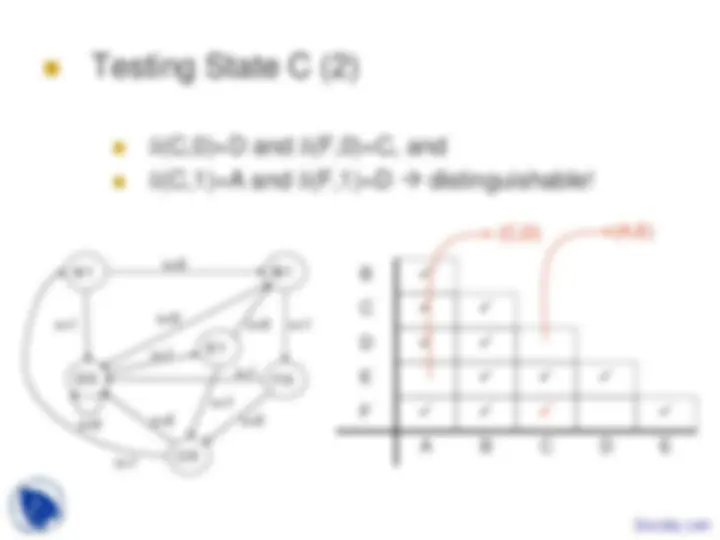
Testing State C (2)
d(C,0)=D and d(F,0)=C, and
d(C,1)=A and d(F,1)=D distinguishable!
B
C
D
E
F
A B C D E
(C,D)^ (A,E)
x=
A/1 B/
x=
D/0 F/
x=
x=
x=
x=
C/
x=0 x=
x=
E/
x=
x=
x=
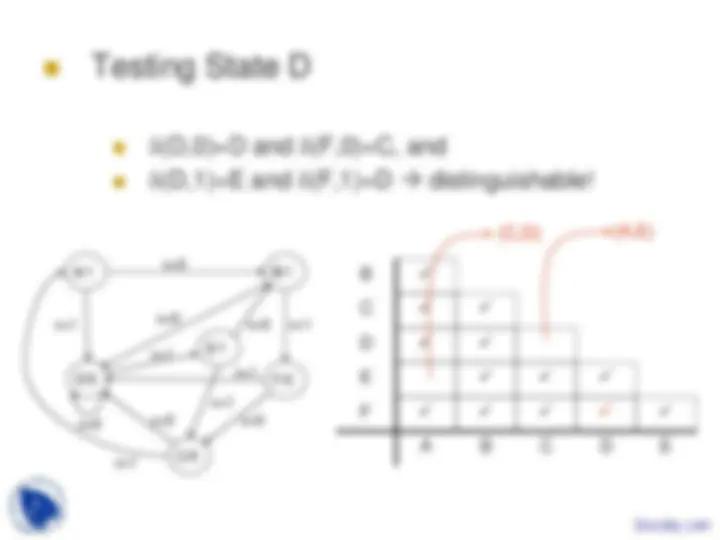
Testing State D
d(D,0)=D and d(F,0)=C, and
d(D,1)=E and d(F,1)=D distinguishable!
B
C
D
E
F
A B C D E
(C,D)^ (A,E)
x=
A/1 B/
x=
D/0 F/
x=
x=
x=
x=
C/
x=0 x=
x=
E/
x=
x=
x=
Resulting Minimal FSM
The Effect of the Outputs Consider the two FSMs:
The only difference is in the output of states C
This FSM cannot be
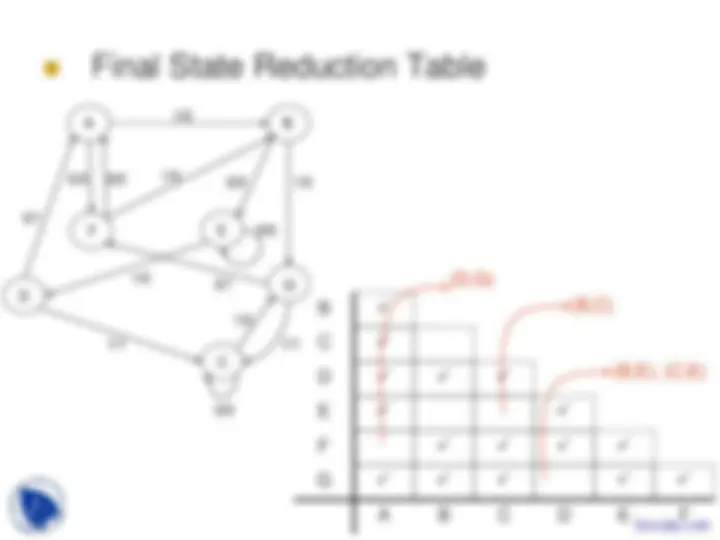
- 00/ How can you automate the reduction in states? - Sense= - 10/ - Sense= - Sense= - 11/ - Sense= - Sense= - Sense= - 01/ - Sense=
- Sense= - 00/ - Sense= - 10/ - Sense= - Sense= - 11/ - Sense=0 Sense= - Sense= - A/ States A and D are equivalent
- S= - B/ - S= - S= - C/ - S= - S= - S= - D/ - S=
- S= - S= - A/ - S= - B/ - S= - S= - C/ - S= - S=
- A/1 B/ - x=
- D/0 F/
- A/1 B/ - x=
- x=1 x= - x= - x= - x= - x=0, - x= and E
- A/1 B/ - x=
- D/0 F/
- A/1 B/ - x=
- x= - x= - x= - x= - C/ - x=0 x= - x= - E/ - x= - x= - x= - x= - A/1 B/ - x= - D/0 F/ - x= - x= - x= - x= - C/ - x=0 x= - x= - E/ - x= - x= - x=
Final State Reduction Table
A B
G
F
C
E
D
B
C
D
E
F
G
A B C D E F
(B,C)
(B,E), (C,E)
(D,G)
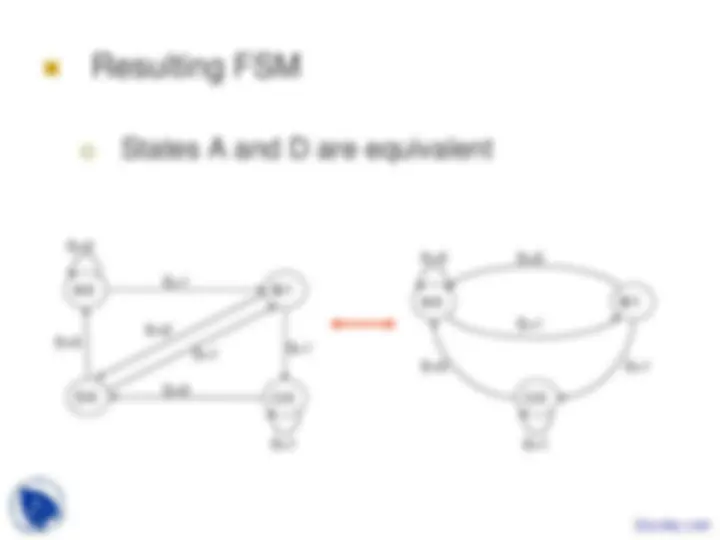
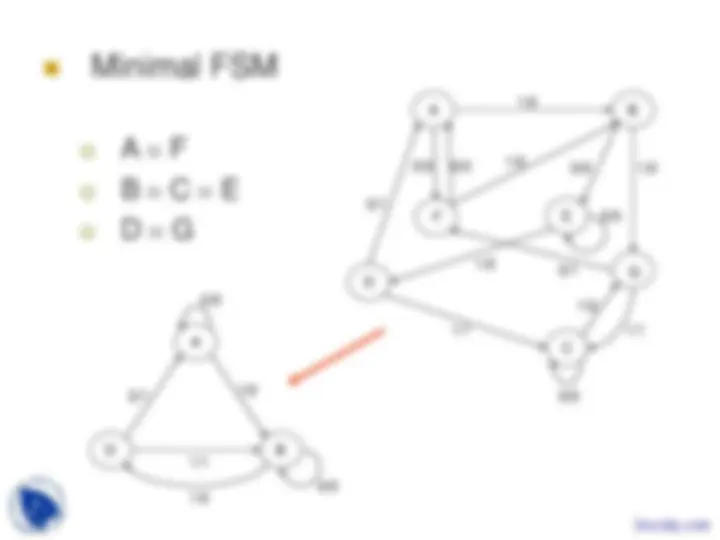
Minimal FSM
A F
B C E
D G