Download Standard Product -Components and Design Techniques for Digital System - Exams and more Exams Digital Systems Design in PDF only on Docsity!
Your Name: _______________________________________
Final Examination Page 1 of 12 CS 150 - Sp. 95
UNIVERSITY OF CALIFORNIA AT BERKELEY BERKELEY • DAVIS • IRVINE • LOS ANGELES • RIVERSIDE • SAN DIEGO • SAN FRANCISCO SANTA BARBARA • SANTA CRUZ Department of Electrical Engineering and Computer Sciences
CS 150 - Spring 1995 Prof. A. R. Newton
Final Examination
(Open Katz, asynchronous & test notes only, Calculators OK, 3 hours)
Include all final answers in locations indicated on these pages. Use space provided for all working. If necessary, attach additional sheets by staple at the end. BE SURE TO WRITE YOUR NAME ON EVERY SHEET.
(1) (18pts) (a) Four chairs are placed in a row: A B C D
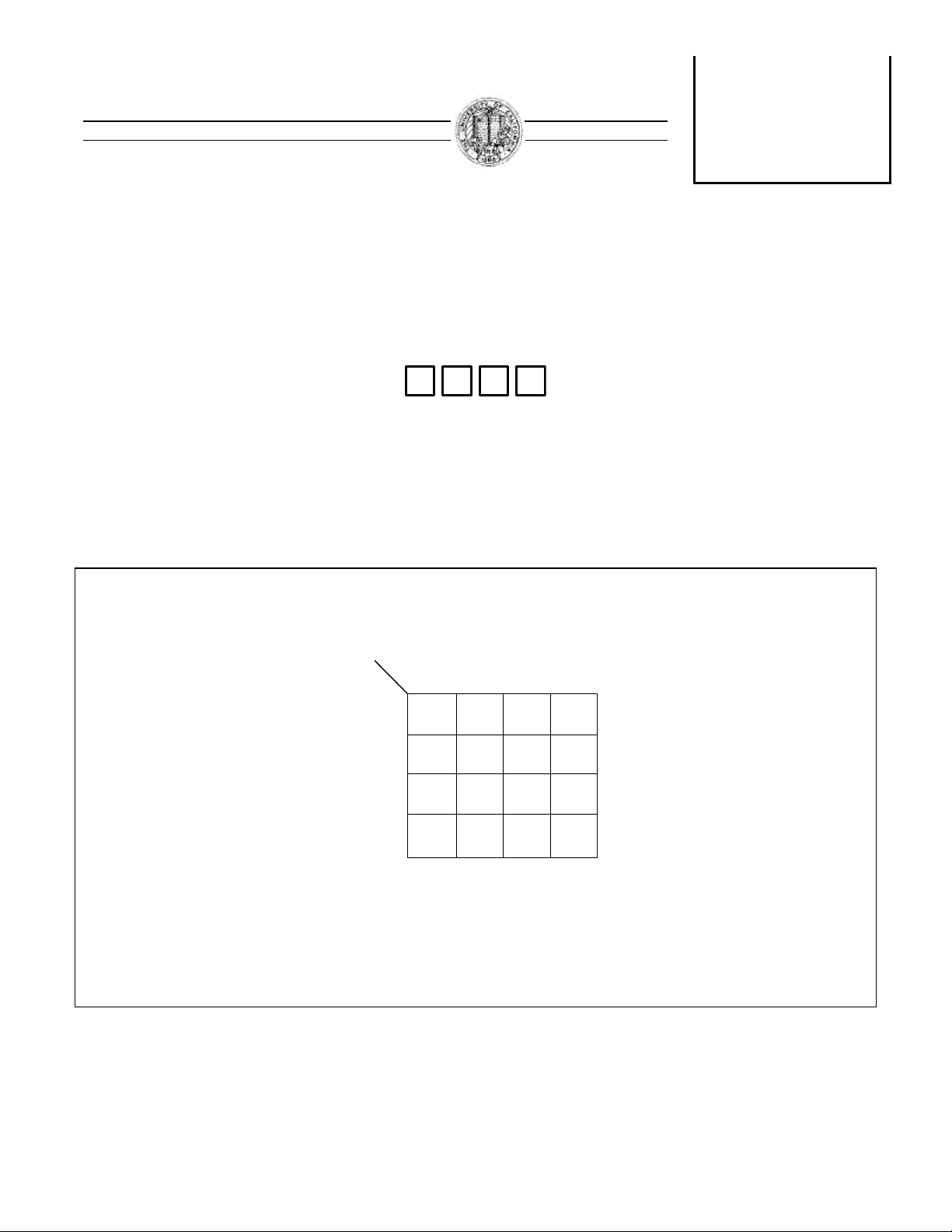
Each chair may be occupied (“1”) or empty (“0”). Write a logic function F(A,B,C,D) which is “1” iff there are two (or more) adjacent chairs that are empty. Express F: (i) As a Karnaugh Map. (ii) In minimum Sum-of-Products form using algebraic notation. (iii) In Standard Sum-of-Products (minterm) form. (iv) In Standard Product of Sums (maxterm) form.
1(a) 9pts (i) F(A,B,C,D) as a Karnaugh Map:
AB
CD 00 01 11 10
(ii) In minimum SoP form, F(A,B,C,D) = ______________________________________
(iii) In Standard SoP form, F(A,B,C,D) = ______________________________________
(iv) In Standard PoS form, F(A,B,C,D) = ______________________________________
TOTAL /
CS 150 - Sp. 95 Page 2 of 12 Final Examination
(b) How many different combinational logic functions of two variables (X and Y) are there?
1(b) 2pts
Total number. of switching functions: __________
(c) Given that:
F(A,B,C,D) = Σm(1,4,5,6,7,9,13,15) Using a Karnaugh Map: (i) List all of the essential prime implicants. (ii) How many prime implicants are there? List them. (iii) How many implicants are there? Just give the number, don’t list them. (iv) Implement the function using a single 8-to-1 MUX and two-input AND gates only. Assume variables and their complements are available. Be sure to label your MUX inputs.
1(c) 7pts
AB CD 00
(^01 11 )
00
01
11
10
(i) Essential prime implicants: ______________________________________
(ii) Prime implicants: ______________________________________________
(iii) Total number of implicants: _________
(iv) Implementation:
CS 150 - Sp. 95 Page 4 of 12 Final Examination
(c) Complete the timing diagram for the circuit shown below. Note that the CK (clock) inputs on the two flip-flops are different. Assume all internal delays are zero and that there are no setup and hold constraints.
2(c) (12pts)
Additional space for Problem 2
Your Name: _______________________________________
Final Examination Page 5 of 12 CS 150 - Sp. 95
(3) (20pts) (a) Construct a state graph for the circuit shown below (X is the input and Z is the output.)
3(a) (6pts)
Additional space for Problem 3
Your Name: _______________________________________
Final Examination Page 7 of 12 CS 150 - Sp. 95
(4) (16pts) (a) Draw the schematic diagram for a minimal hazard-free realization (gates + gate inputs) of the following function using only 3-input NOR gates. Assume variables and their complements are available.
F(A,B,C,D) = Σm(0, 2, 6, 7, 8, 10, 13)
4(a) (6pts)
Additional space for Problem 4
CS 150 - Sp. 95 Page 8 of 12 Final Examination
(b) For the flow table shown below, find a state assignment that avoids all critical races. Additional states may be added as necessary, but use as few state variables as possible. Assign the all-0’s combination to state A. If any additional states are needed to prevent critical races, use your state assignment and adjacency map to explain why.
Sn 00 01 11 10 A B C – A B B E – B C F C – E D D F – B E D E – E F F F – A
Sn+
XY
4(b) (10pts)
State assignment: _______________________________________________________________
Adjacency map:
CS 150 - Sp. 95 Page 10 of 12 Final Examination
(c) Add the following numbers in base-(-2). Pay close attention to the carry-in and carry-out aspects because they are important in Part (d)
5(c) (2pts)
001110 -2 + 001111-2 = ______________ -
(d) Draw a truth table for a one-bit bit slice of a base-(-2) adder. Assume one bit of carry-in. You must determine the specification for the carry-out.
5(d) (3pts)
(e) Repeat part (d) above but with two carry-in bits.
5(e) (3pts)
Your Name: _______________________________________
Final Examination Page 11 of 12 CS 150 - Sp. 95
(f) Draw the block-diagram for a 4-bit base-(-2) adder, using your one-bit bit slice from 5(e) above.
5(f) (4pts)
Additional space for Problem 5
