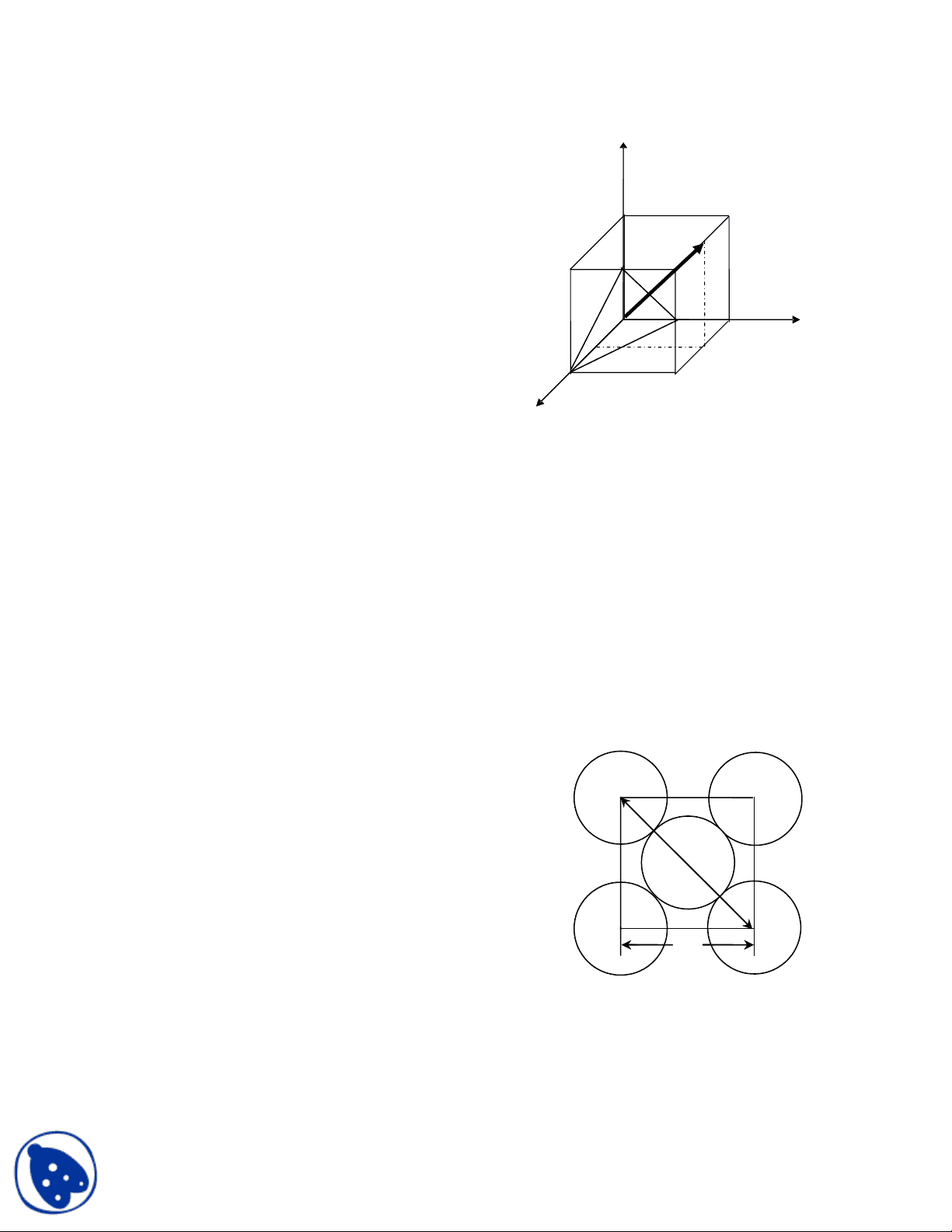
1. Draw a space lattice of simple cubic lattice,
then
a) Find out the (122) plane and [122]
direction
b) Calculate the angle between (122) plane
and [122] direction
Answer: (a) See the attached figure for (122)
plane and [122]
(b) cos
θ
= (1
×
1 + 2
×
2 +
2
×
2)/
√
(12+22+22)2
= 1
then
θ
= 0o (note: people use normal line of a plane to represent the plane)
2. The density of aluminum (Al), which has the fcc structure, is 2.70g/cm3. The atomic
weight of aluminum is 26.98g/mol. Calculate
a) The lattice constant of aluminum
b) The atomic radium of aluminum
Answer: (a) mass of one Al atom = (26.98 g/mol) / (6.02
×
10 23atoms/mol)
= 4.48
×
10-23g/atom
density = (mass of unit cell)/(volume of unite cell)
For fcc: density = (mass of 4 atoms)/a3
Then 2.7 g/cm3 = 4
×
(4.48
×
10-23g)/ a3
a = 4.05
×
10-8 cm
(b) Look at the diagonal line of fcc’s
[100] plane,
√
2 a = 4
×
r
r =
√
2 a/4 = 1.43
×
10 -8 cm
4r
a
Y
X
Z
O
Docsity.com