Small World Networks Two - Complex Networks - Lecture Slides, Slides of Data Communication Systems and Computer Networks

Download Small World Networks Two - Complex Networks - Lecture Slides and more Slides Data Communication Systems and Computer Networks in PDF only on Docsity!

Lecture 18:

Small World Networks

Docsity.com

Outline

• Small world phenomenon
  • Milgram’s small world experiment
• Small world network models:
  • Watts & Strogatz (clustering & short paths)
  • Kleinberg (geographical)
  • Watts, Dodds & Newman (hierarchical)
• Small world networks: why do they arise?
  • efficiency
  • navigation

Docsity.com

NE

MA

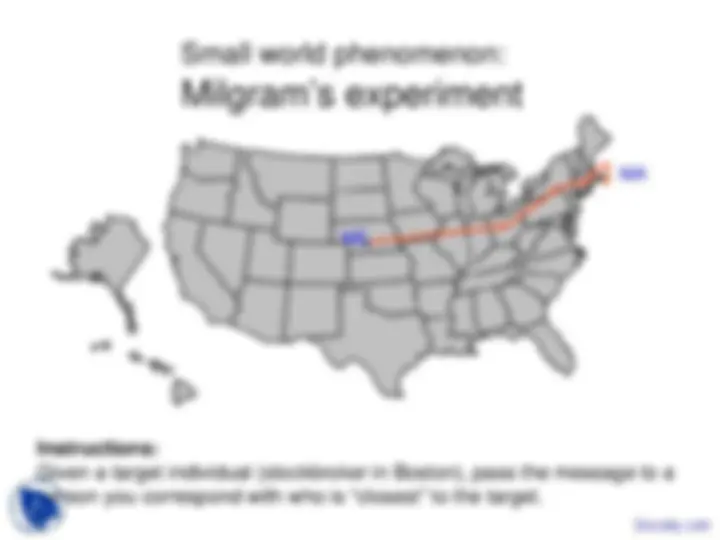
Small world phenomenon: Milgram’s experiment

“Six degrees of separation”

Outcome: 20% of initiated chains reached target average chain length = 6.

Docsity.com

email experiment Dodds, Muhamad, Watts, Science 301, (2003)

•18 targets •13 different countries

•60,000+ participants •24,163 message chains •384 reached their targets •average path length 4.

Small world phenomenon: Milgram’s experiment repeated

Source: NASA, U.S. Government; http://visibleearth.nasa.gov/view_rec.php?id=2429 Docsity.com

Small world experiment: accuracy of distances

 Is 6 an accurate number?

 What bias is introduced by uncompleted chains?

 are longer or shorter chains more likely to be completed?

 if each person in the chain has 0.5 probability of passing the letter on, what is the likelihood of a chain being completed  of length 2?  of length 5?

Docsity.com

average 95 % confidence interval

Small world experiment accuracy: attrition rate is approx. constant

probability of passing on message^ position in chain

Source: An Experimental Study of Search in Global Social Networks: Peter Sheridan Dodds, Roby Muhamad, andDuncan J. Watts (8 August 2003); Science 301 (5634), 827. Docsity.com

Small world experiment: accuracy of distances

• Is 6 an accurate number?
• Do people find the shortest paths?
  • The accuracy of small-world chains in social networks by Killworth et.al.
  • less than optimal choice for next link in chain is made ½ of the time

Docsity.com

Small world phenomenon: business applications?

“Social Networking” as a Business:

• FaceBook, MySpace, Orkut, Friendster entertainment, keeping and finding friends
• LinkedIn: •more traditional networking for jobs
• Spoke, VisiblePath •helping businesses capitalize on existing client relationships Docsity.com

Outline

Small world phenomenon

Milgram’s small world experiment

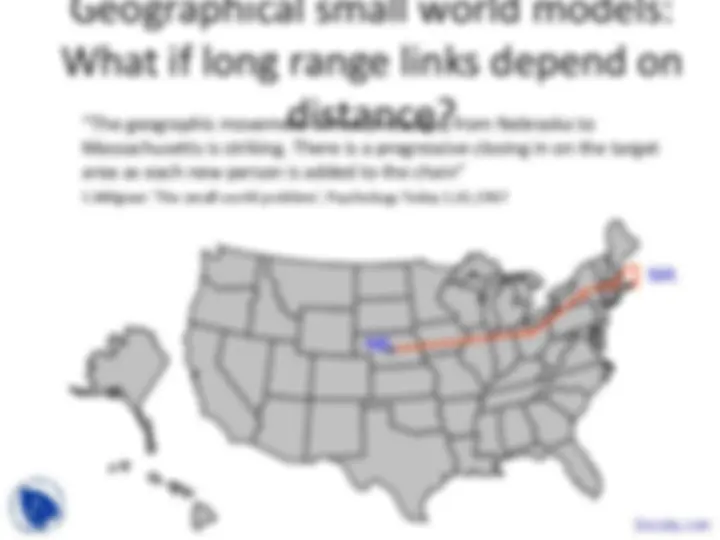
Small world network models:

Watts & Strogatz (clustering & short paths) Kleinberg (geographical) Watts, Dodds & Newman (hierarchical)

Small world networks: why do they arise?

efficiency Docsity.com

Reconciling two observations:

• High clustering: my friends’ friends tend to be my friends
• Short average paths

Small world phenomenon: Watts/Strogatz model

Source: Watts, D.J., Strogatz, S.H.(1998) Collective dynamics of 'small-world' networks. Nature 393:440-442. Docsity.com

• Each node has K>=4 nearest neighbors (local)
• tunable: vary the probability p of rewiring any given edge
• small p : regular lattice
• large p : classical random graph

Watts-Strogatz model: Generating small world graphs

Docsity.com

Watts/Strogatz model:

What happens in between?

• Small shortest path means small clustering?
• Large shortest path means large clustering?
• Through numerical simulation
  • As we increase p from 0 to 1
    • Fast decrease of mean distance
    • Slow decrease in clustering

Docsity.com

Watts/Strogatz model: Clustering coefficient can be computed for SW model with rewiring

• The probability that a connected triple stays connected after rewiring - probability that none of the 3 edges were rewired (1-p) 3 - probability that edges were rewired back to each other very small, can ignore
• Clustering coefficient = C(p) = C(p=0)*(1-p) 3

0.2 0.4 0.6 0.8 1

1

C(p)/C(0)

Source: Watts, D.J., Strogatz, S.H.(1998) Collective dynamics of 'small-world' networks. Nature 393:440-442.^ p Docsity.com

Watts/Strogatz model:

Clustering coefficient: addition of

random edges

• How does C depend on p?
• C’(p)= 3xnumber of triangles / number of connected triples
• C’(p) computed analytically for the small world model without rewiring^2 (^2 1 )^4 (^2 )

' ( )^3 (^1 ) − + + = − k kp p C p k

0.2 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1

1

p

C’(p)

Source: Watts, D.J., Strogatz, S.H.(1998) Collective dynamics of 'small-world' networks. Nature 393:440-442. Docsity.com