SIMU SIMU NOTES FOR BE seventh semester student, Lecture notes of Mathematical Modeling and Simulation

Download SIMU SIMU NOTES FOR BE seventh semester student and more Lecture notes Mathematical Modeling and Simulation in PDF only on Docsity!

Physical and Mathematical Models

By: Prof S ShakyaProf. S. Shakya

Static Physical ModelsStatic Physical Models ^ The best known examples of physical models are scalemodels. ^ In shipbuilding, making a scale model provides a simple wayof determining the exact measurements of the platesof determining the exact measurements of the platescovering the hull, rather than having to produce drawings ofcomplicated, three-dimensional shapes.

p^

p

Static Physical ModelsStatic Physical Models ^ Although air is blown over the model, or the model is pulledthrough the water, these are static physical models becausethe measurements that are taken represent attributes of thesystem being studied under one set equilibrium conditionssystem being studied under one set, equilibrium conditions. ^ In this case, the measurements do not translate directly intosystem attribute values.

y

Static Physical ModelsStatic Physical Models ^ Well known laws of similitude are used to convertmeasurements on the scale model to the values that wouldoccur in the real system. ^ Sometimes a static physical model is used as a means of^ Sometimes, a static physical model is used as a means ofsolving equations with particular boundary conditions. ^ There are many examples in the field of mathematical physics

y^

p^

p y

where the same equations apply to different physicalphenomena.

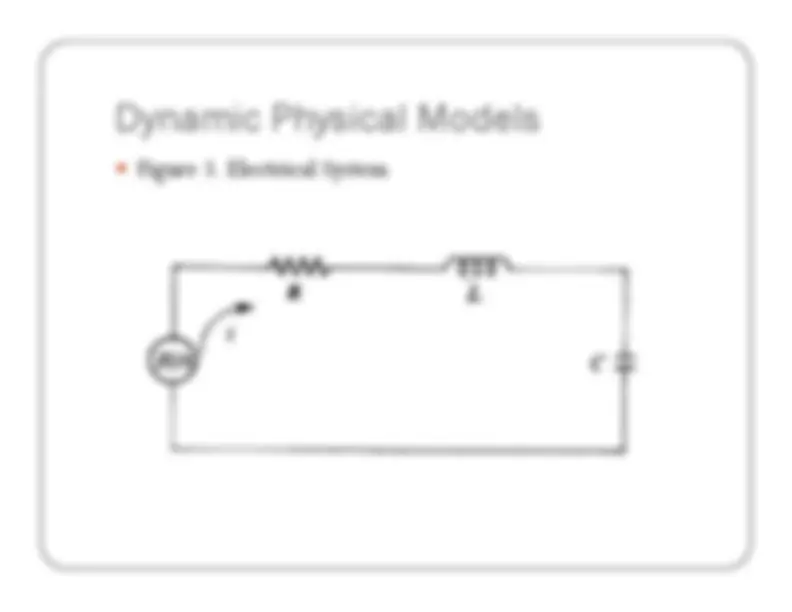
Dynamic Physical ModelsDynamic Physical Models ^ Dynamic physical models rely upon an analogy between thesystem being studied and some other system of a differentnature, the analogy usually depending upon an underlyingsimilarity in the forces governing the behavior of the systemssimilarity in the forces governing the behavior of the systems. ^ To illustrate this type of physical model, consider the twosystems shown in following figures i.e. Figure 2 and Figure 3.

y^

g^

g^

g^

g

Dynamic Physical ModelsDynamic Physical Models ^ Figure 2. Mechanical System

Dynamic Physical ModelsDynamic Physical Models ^ The Figure 2. represents a mass that is subject to an appliedforce F(t) varying with time, a spring whose force isproportional to its extension or contraction, and a shockabsorber that exerts a damping force proportional to theabsorber that exerts a damping force proportional to thevelocity of the mass. ^ The system might for example represent the suspension of an

y^

g^

p^

p^

p

automobile wheel when the automobile body is assumed tobe immobile in a vertical direction.

Dynamic Physical ModelsDynamic Physical Models ^ It can be shown that the motion of the system is described byth

f ll

i^

diff

ti l

ti

the following differential equation. Where,x is the distance moved,M is the mass,K is the stiffness of the spring,D is the damping factor of the shock absorber

Dynamic Physical ModelsDynamic Physical Models ^ Inspection of these two equations shows that they haveexactly the same form and that the following equivalencesoccur between the quantities in the two systems:

Dynamic Physical ModelsDynamic Physical Models Displacement

x

Charge q

Velocity

Current I(= )

Force F

Voltage E

Mass

M

Inductance L

Damping factor D

Resistance

R

Spring stiffness

K

1/Capacitance 1/C

Dynamic Physical ModelsDynamic Physical Models ^ If, for example, a car wheel is considered to bounce toomuch with a particular suspension system, the electricalmodel will demonstrate this fact by showing that the charge(and therefore the voltage) on the condenser oscillates(and, therefore, the voltage) on the condenser oscillatesexcessively. ^ To predict what effect a change in the shock absorber or

p^

g

spring will have on the performance of the car, it is onlynecessary to change the values of the resistance or condenseri^ th

l^ t i^

l^ i

it^

d^

b^

th^

ff^

t^

th^

th

in the electrical circuit and observe the effect on the way thevoltage varies.

Dynamic Physical ModelsDynamic Physical Models ^ If in fact, the mechanical system were as simple as illustrated,it could be studied by solving the mathematical equationderived in establishing the analogy. ^ However effects can easily be introduced that would make^ However, effects can easily be introduced that would makethe mathematical equation difficult to solve.

Static Mathematical ModelStatic Mathematical Model ^ For example, in marketing a commodity there is a balancebetween the supply and demand for the commodity. ^ Both factors depend upon price: a simple market mode! willshow what is the price at which the balance occursshow what is the price at which the balance occurs. ^ Demand for the commodity will be low when the price ishigh, and it will increase as the price drops.

g ,

p^

p.

Static Mathematical ModelStatic Mathematical Model ^ The relationship between demand, denoted by Q, and price,denoted by P might be represented by the straight line markeddenoted by P, might be represented by the straight line marked"Demand“ in Figure 4. ^ On the other hand, the supply can be expected to increase as theprice increases, because the suppliers see an opportunity for moreprice increases, because the suppliers see an opportunity for morerevenue. ^ Suppose supply, denoted by S, is plotted against price, and therelationship is the straight line marked "Supply" in Figure 4.lf

p^

g^

pp y

g

conditions remain stable, the price will settle to the point at whichthe two lines cross, because that is where the supply equals thedemand.  Since the relationships have been assumed linear, the completemarket model can be written mathematically as follows: