Markov Chains: Probability Models for Discrete Systems, Study notes of Mathematical Modeling and Simulation

Download Markov Chains: Probability Models for Discrete Systems and more Study notes Mathematical Modeling and Simulation in PDF only on Docsity!

Markov ChainsProf. S. Shakya

Markov Chains  If the future states of a process are independent of the If the future states of a process are independent of thepast and depend only on the present , the process iscalled a Markov process  A discrete state Markov process is called a Markovchain.A Markov Chain is a random process with the property A^ Markov Chain is a random process with the propertythat the next state depends only on the current state.

M^

k^

Ch i

Markov Chain ^ A simple example is the nonreturningrandom walk, where the walkers arerestricted to not go back to the locationjust previously visited.

M^

k^

Ch i

Markov Chains ^ Markov chains is a mathematical tools forstatistical modeling in modern applied

g^

pp

mathematics, information science

M^

k^

Ch i

Markov ChainsAs we have discussed, we can view a stochastic processas sequence of random variables

{X^ ,X^12

,X^ ,X^34

,X^ ,X^56

,X^ ,.. .}^7

Suppose that X

depends only on X 7

, X^ depends only 66 f^

f f

on X^5 , X^ on X^5

, and so forth. In general, if for all i,j,n, 4

P(X^ n+

=^ j |x n

=^ i , x n

=^ n− 1 i ,... , xn−^1

=^ i ) = P(X 0 0

=^ j n+ |X^ =^ n^ i ),n

then this process is what we call a Markov chain

.

Markov ChainsMarkov

Chains

•The conditional probability above gives us the probability thatThe conditional probability above gives us the probability thata process in state i

at time n moves to in

at time n + 1.n+

•We call this the transition probability for the Markov chain.If th^

t^ iti

b bilit

d^

t d^

d^ th

ti

•If the transition probability does not depend on the time n, wehave a stationary Markov chain, with transition probabilities^ Now we can write down the whole Markov chain as a matrix P:Now we can write down the whole Markov chain as a matrix P:

Key Features of Markov ChainsKey

Features of Markov Chains

^ A sequence of trials of an experiment is a^ Markov chain

if

Markov

chain

if

1) the outcome of each experiment

is one of a set of discrete states;is one of a set of discrete states;

2) the outcome of an experimentd

d^

l^

th^

t^ t t

depends only on the present state,and not on any past states;3) the transition probabilities remainconstant from one transition to thenext.

M^

k^

Ch i

Markov Chains ^ The Markov chain has network structure much like thatof website, where each node in the network is called astate and to each link in the network a transitionstate and to each link in the network a transitionprobability is attached, which denotes the probability ofmoving from the source state of the link to its destinationstate.

I t^

t^

li^

ti

Internet application ^ The PageRank of a webpage as used by Google isdefined by a Markov chain.It i^

th^

b bilit

t^ b

t^

i^ i^ th^

t ti

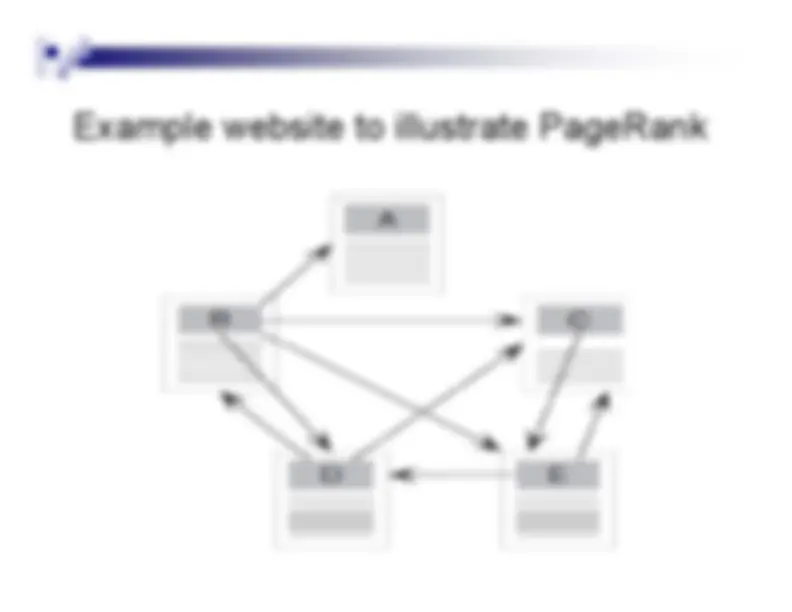
^ It^ is the probability to be at page

i^ in the stationary

distribution on the following Markov chain on all (known)webpages. If

N^ is the number of known webpages, and a p g^

p g

page^

i^ has^ ki links then it has transition probability^ f^ ll

th t^

li k d t

d

f^ ll

th t

for all pages that are linked to and

for all pages that

are not linked to.  The parameter

α^ is taken to be about 0 85

^ The parameter

α^ is taken to be about 0.

I t^

t^

li^

ti

Internet application ^ Markov models have also been used to analyzeweb navigation behavior of users. ^ A user's web link transition on a particularwebsite can be modeled using first- or second-dorder ^ Markov models and can be used to make

di ti^

di^

f t^

i^ ti^

d t

predictions regarding future navigation and topersonalize the web page for an individual user.

E^

l^

f^

k^ i k

Example of a rank sink

Markov ProcessMarkov

Process

• Markov Property:

The state of the system at time

t +1^ depends only

on the state of the system at time

t y

^

^

^

 x

| Xx X xx X | Xx X^

tt t t t t t t^

^

 

 ^

1 1

1 (^11) 1

Pr

Pr^

X^1

X^2

X^3

X^4

X^5

• Stationary Assumption:

Transition probabilities are independent of

time ( t

)

^

P^ X^

b| X

^

1 Pr^ t^

t^

ab

X^

b^ | X^

a^ p ^ 

^ 

Markov ProcessSi^

l^ E^

l

Simple Example^ Weather:^ •^ raining today

40% rain tomorrow60% no rain tomorrow

-^ not raining today

20% rain tomorrow80% no rain tomorrow80% no rain tomorrow

^ 

-^ Stochastic matrix:

The transition matrix:

P^

-^ Stochastic matrix:^ Rows sum up to 1• Double stochastic matrix:Rows and columns sum up to 1Rows and columns sum up to 1

Markov ProcessC k^

P^

i E^

l

Coke vs. Pepsi Example^ • Given that a person’s last cola purchase was Coke,there is a 90% chance that his next cola purchase will^ there is a

90%^

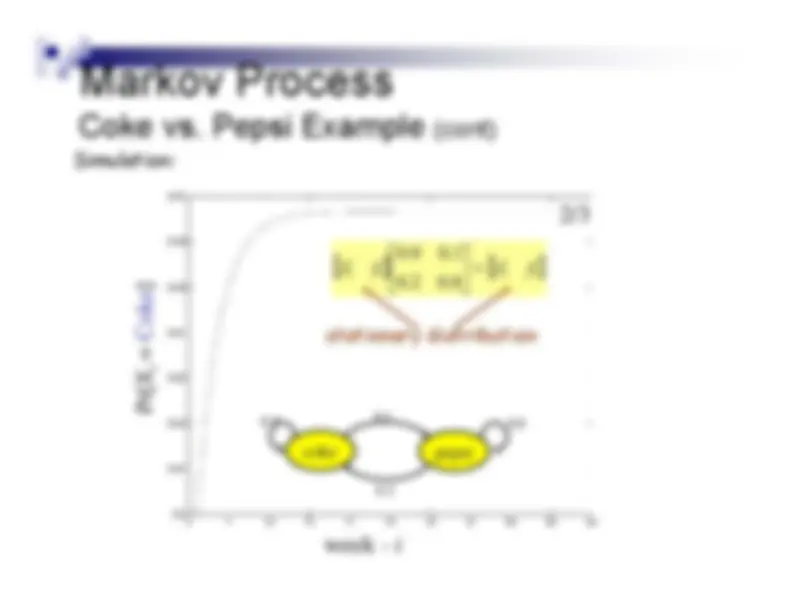
chance that his next cola purchase will also be Coke.• If a person’s last cola purchase was Pepsi, there isIf a person s last cola purchase was

eps , there s

an 80% chance that his next cola purchase will also bePepsi.

0.^

^

transition matrix:

coke^

pepsi

P