SIGNALS AND SYSTEMS QUIZ 3 ECE, Quizzes of Signals and Systems

Download SIGNALS AND SYSTEMS QUIZ 3 ECE and more Quizzes Signals and Systems in PDF only on Docsity!

Ans:

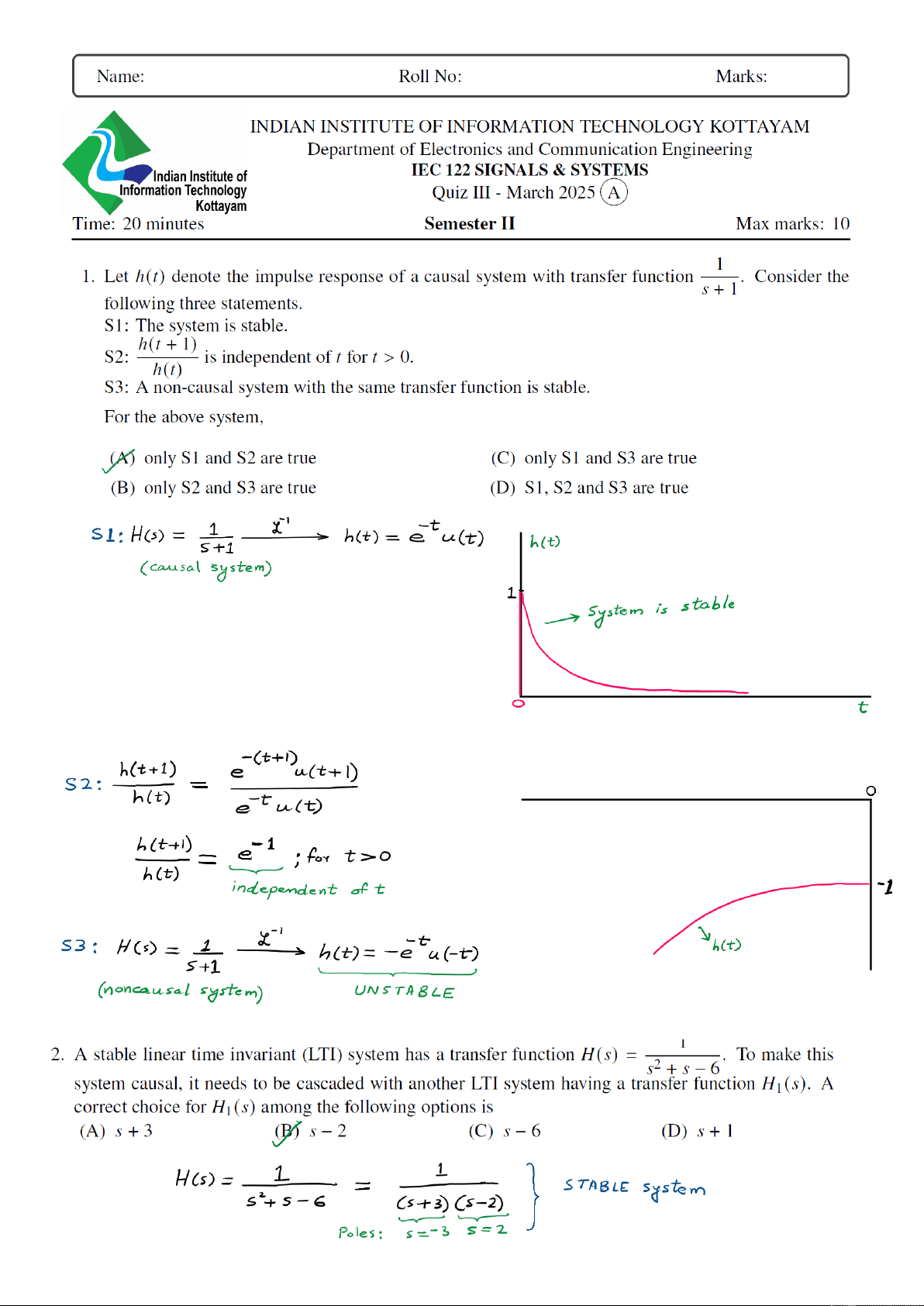
Name: Roll No: Marks: INDIAN INSTITUTE OF INFORMATION TECHNOLOGY KOTTAYAM Department of Electronics and Communication Engineering Indian Institute of TEC 122 SIGNALS & SYSTEMS Information Technology Quiz III - March 2025 (A) Kottayam ~~ Time: 20 minutes Semester IT Max marks: 1() . . . 1 . 1. Let A(t) denote the impulse response of a causal system with transfer function ——. Consider the y following three statements. S1: The system is stable. Ait+d). . 2: hl is independent of t for t > 0. $3: A non-causal system with the same transler function is stable. For the above system, VI only S1 and S2 are true (C) only SI and S3 are true (B) only $2 and $3 are true (D) S1, 82 and $3 are true Ans: A = 1 xt! _ oot Sl: He = Sq ON) = ee) Ccosssal system) h(t+1) _ oad ha) erucd bees) e! tfor THO h(t) ——~ indepemdent of t z= -1 S3: W@®= 2 4. pp Stu need S41 (honcausal sgstem) UNSTABLE 2. A stable linear time invariant (LTI) system has a transfer function H(s) = _—. To make this sets system causal, it needs to be cascaded with another LT! system having a transfer function H)(s). A correct choice for H)(s) among the following options is (A) s+3 (BS 5-2 (C) s-6 (D) s+1 Ans: 1 Hays —_1L = = STABLE system s4s-6 Cs+3) Cs—2) ee ee Poles: sard S52 To make the system both causal and stable, no poles of Hes) Shall lie on left-half of s-plane. Hence Cs-2) term in the denominator has fo be removedk using Hy €5)- H\G)=G-2) oe ) - LL. $+2 eos STABLE + CAUSAL 4 Hes Ganei Cc L 3. The transfer function of an LTI system is given by ay = var For the input r(f) = sin r, the y steady-state response c(/) is (A) 1 (B) scos t (C) S| in t+ = Ws —ssin (ft — V2 v2 ( 4 ) 4 Ans: Gwen the TF, Hos)= Sey it Res) s+i . L The. Prequency vesponse i's gen by Hy) = joi The input signal is Ct) = stn(t) wel Acjal= i > LHGw) = O-Tan (2) = —Tan() fost+4 [Hoe =tL 57 Hg) = -Ton'(/) = -Z Oo =F? ; Joost a vit)=sint DP} HGiw) p> . Gs) = «?* . He). s Hos) +o Hes) a 0 Gis)= Hts) + THES HWS Ss _ L t+ SOS SHA S+06> s ie, Gos) = t= Single Pele :s=0 7. The Laplace transform of a causal signal y(r) is ¥(s) = aes The value of the signal y(t) att = 0.1s ig —2-19S | st Ans: Yosye 242 ~ 546-4 _ 1-4 s+6 s+6 S+é -1 -s6t a y@= t[t- S]= sense ee, Causal Signal 9c| 8. For a system having transfer function G(s) = - _ 46 CO) _ = = 46 °S= 2.195 t=0-Llsec . 4 unit step input is applied at t = 0. The value of the response of the system at t = 1.5 sec (rounded off to three decimal places) is_ 0-554 Ans: Gos) = Sst. sti x(t) = ult)<%~ > Xoy= 4 Yos)= X0s)-Gisy= TS+h . A ° s(s+1) Ss 1 S41 Yoo = LB A- ~stl) 21 s s+1 S41 |s-6 git) = A-26°*) ue) os Ss |s=-1 ys) = (1-2e7*) = Ose 2 9. Consider a system with transfer function G(s) = ——. A unit step function u(t) is applied to the system, which results in an output y(7). If e(¢) = yin q(t), then jim e(t)is 4 Ans: ~2vit ~i.2 pe Yes) = XO8)-Ge = ss = yie) -p)<*£> Es ¥oy- 2 Lf2 -1] = 455 e(t)= ge) ‘aa = MCs st SLi Sd+5) lim e(t) = lim 2.6) = fim s+ Oro _ 4 t>% 5-90 ~e S(its) — 10. The signal x(4) = (¢ — 1)?u(¢ — 1), where (1) is the unit-step function, has the Laplace transform X(s). The value of X(1) is O-°736. Ans: Baty te "50 trum» 4 _ 2. Time -Shitt, stl s3 Roperty -s x= C-DuG-p Ao Kore 2; =I “X= @ +2 _ 2 = 0.736 13 e