Set Theory - Discrete Mathematics - Lecture Slides, Slides of Discrete Mathematics

Download Set Theory - Discrete Mathematics - Lecture Slides and more Slides Discrete Mathematics in PDF only on Docsity!

CS 173:

Discrete Mathematical Structures

Set Theory - A proof for us to do together.

Pv that if (A - B) U (B - A) = (A U B)

then ______

Suppose to the contrary, that A ∩ B ≠ ∅, and that x ∈ A ∩ B.

Then x cannot be in A-B and x cannot be in B-A.

Do you see the contradiction yet? But x is in A U B since (A ∩ B) ⊆ (A U B).

A ∩ B = ∅

Thus, A ∩ B = ∅.

a) A U B = ∅ b) A = B c) A ∩ B = ∅ d) A-B = B-A = ∅ Then x is not in (A - B) U (B - A).

DeMorgan’s!!

Trying to pv p --> q Assume p and not q, and find a contradiction. Our contradiction was that sets weren’t equal.

Set Theory - Generalized Union

Ai

i = 1

n

 =^ A^1 ∪^ A^2 ∪^ ^ ∪^ A^ n

Ex. Let U = N , and define:

Ai = { x : ∃ k > 1, x = ki , k ∈ Ν}

Then



Ai i = 2

∞

 =^?

a) Primes b) Composites c) ∅ d) N e) I have no clue.

primes

Set Theory - Generalized Intersection

Ai

i = 1

n  =^ A^1 ∩^ A^2 ∩^ ^ ∩^ A^ n

Ex. Let U = N , and define:

Ai = { x : ∃ k , x = ki , k ∈ Ν}

A 1 = {1,2,3,4,…} A 2 = {2,4,6,…} A 3 = {3,6,9,…}

Set Theory - Inclusion/Exclusion

Example:

How many people are wearing a watch?

How many people are wearing sneakers?

How many people are wearing a watch OR sneakers?

What’s wrong?

B A

Wrong.

|A ∪ B| = |A| + |B| - |A ∩ B|

Set Theory - Inclusion/Exclusion

Example:

There are 217 cs majors.

157 are taking cs125.

145 are taking cs173.

98 are taking both.

How many are taking neither?

125 173

Set Theory - Inclusion/Exclusion

Example:

How many people are wearing a watch?

How many people are wearing sneakers?

How many people are wearing a watch AND sneakers?

How many people are wearing a watch OR sneakers?

Set Theory - Generalized Inclusion/Exclusion

For sets A 1 , A 2 ,…An we have:

Ai i = 1

n  =^ Ai 1 ≤ i ≤ n

∑ −^ Ai ∩^ A^ j 1 ≤ i < j ≤ n

∑ +^ ^ +^ (−1) n^ Ai i = 1

n 

Set Theory - Sets as bit strings

Ex. If U = {x1 , x2, x3, x 4 , x 5 , x 6 }, A = {x 1 , x 3 , x 5 , x 6 }, and B = {x 2 , x3, x 6 },

Then we have a quick way of finding the characteristic vectors of A ∪ B and A ∩ B.

A 1 0 1 0 1 1

B 0 1 1 0 0 1

A ∪ B A ∩ B

Bit-wise OR Bit-wise AND

Functions

Suppose we have:

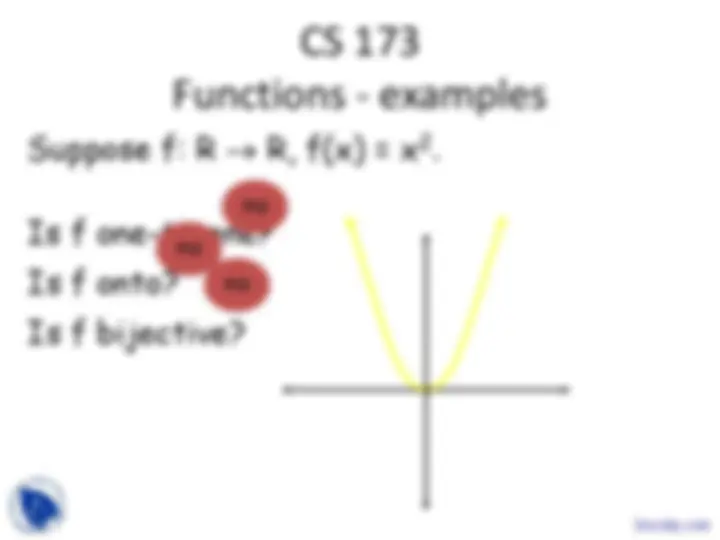
And I ask you to describe the yellow function.

Notation: f: R→R, f(x) = -(1/2)x - 25

What’s a function? f(x) = -(1/2)x - 25

domain co-domain

Functions

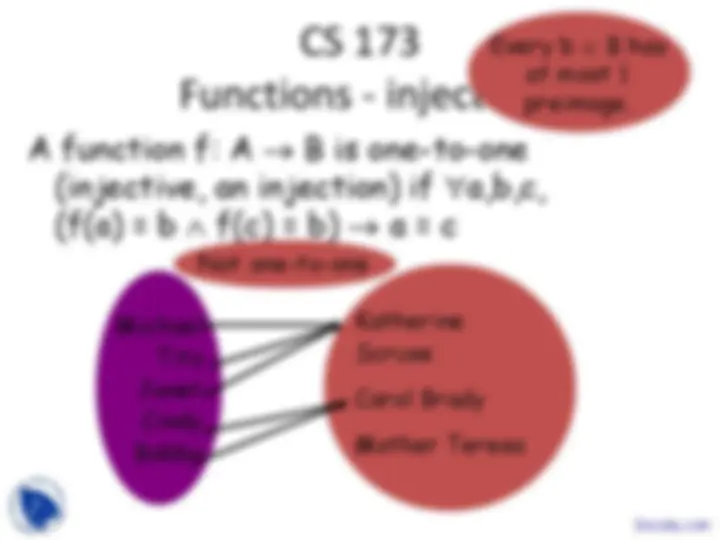
Definition: a function f : A → B is a

subset of AxB where ∀ a ∈ A, ∃! b ∈ B

and <a,b> ∈ f.

A

B

A

B

A point!

A collection of points!

Functions

A = {Michael, Tito, Janet, Cindy,

Bobby}

B = {Katherine Scruse, Carol Brady,

Mother Teresa}

Let f: A → B be defined as f(a) =

mother(a).

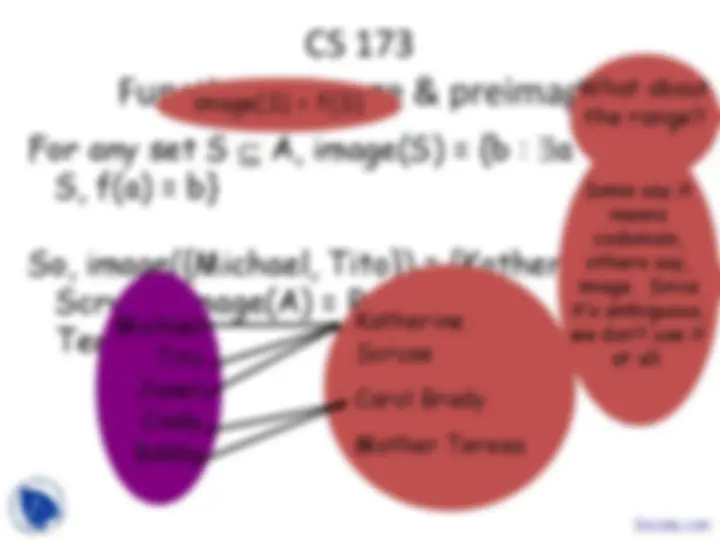
Michael Tito Janet Cindy Bobby

Katherine Scruse

Carol Brady

Mother Teresa

Functions - image & preimage

For any S ⊆ B, preimage(S) = {a: ∃b ∈

S, f(a) = b}

So, preimage({Carol Brady}) = {Cindy,

Bobby} preimage(B) = A

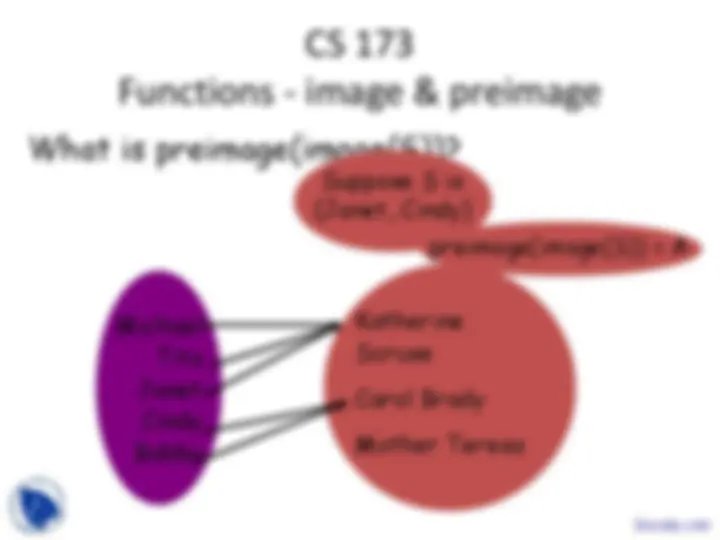
preimage(S) = f -1^ (S)

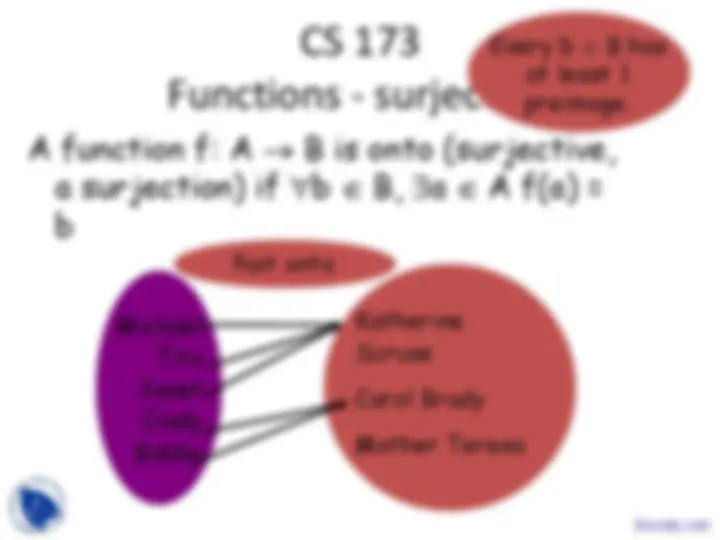
Michael Tito Janet Cindy Bobby

Katherine Scruse

Carol Brady

Mother Teresa

Functions - image & preimage

What is image(preimage(S))?

a) S b) { } c) subset of S d) superset of S e) who knows?

⊆ S

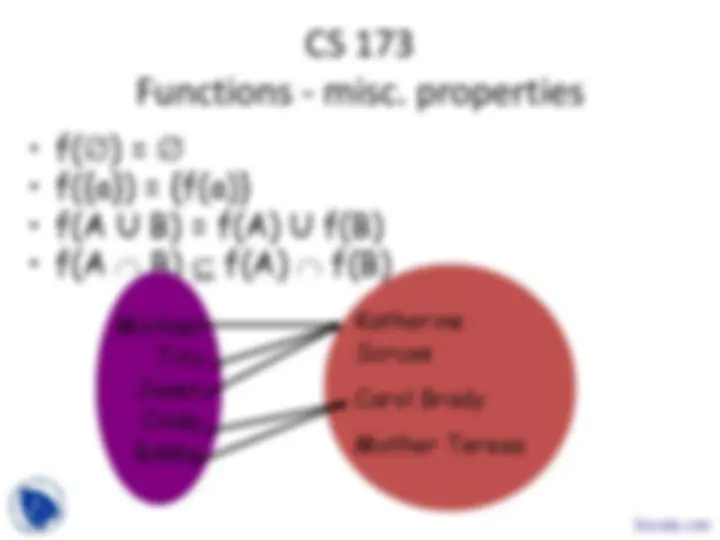
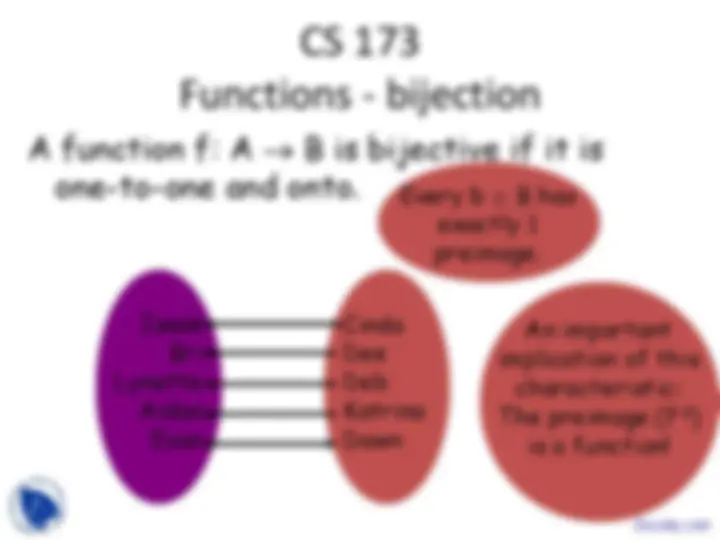
Michael Tito Janet Cindy Bobby

Katherine Scruse

Carol Brady

Mother Teresa