Selection Models, Models for Counts - Econometric Analysis of Panel Data - Lecture Slides, Slides of Econometrics and Mathematical Economics

Download Selection Models, Models for Counts - Econometric Analysis of Panel Data - Lecture Slides and more Slides Econometrics and Mathematical Economics in PDF only on Docsity!

Econometric Analysis of Panel Data

23. Selection Models, Models for Counts,

Hazard Models, Dynamic Models

Canonical Sample Selection Model

Regression Equation

y*=x +

Sample Selection Mechanism

d=z +u; d=1[d > 0] (probit)

y = y* if d = 1; not observed otherwise

Is the sample 'nonrandomly selected?'

E[y*|x,d=1] = x +E[ | x, d 1]

= x +E[ | x,u z ]

= x something if Cor[ ,u|x] 0

A left out variable problem (again)

Incidental truncation

Two Step Estimation

i i i i

i

Step 1: Estimate the probit model

d *= +u ; d =1[d * > 0] (probit).

Estimation of by. Now compute

Step 2: Estimate the regression model with estimated re

φ

λ = 

φ

i

i

i

z γ

z γ

γ γ

z γ

i i

i i i

i i i i i i

i

i i i

gressor

y *= +

y = y * if d = 1; not observed otherwise

E[y *|x ,d =1] = +E[ | x , d 1]

Linearly regress y on x ,.

Step2a. Fix standard errors (Murphy

ε

ε =

• θλ

λ

i

i

i

x β

x β

x β

and Topel). Estimate

and using and /n

ρ

σ θ e'e

The “LAMBDA”

FIML Estimation

i

d 0

2

i i i

2 d 1

2

i i

2

d 0

2

2

i i i

d

logL log

log exp

y

Let

logL log

log exp y ( 1 ) ( y )

=

=

=

=

= Φ − γ

−ε γ + ρε σ

σ

 σ π 

− ρ  

ε = −

ρ

θ = σ δ β σ τ

ρ

= Φ − γ

 θ   

• θ + Φ + τ γ + τ θ +

π  

 

i

i

i i

z

z

x β

z

x δ z x δ

1

Note : no inverse Mills ratio appears anywhere in the model.

Panel Data Extensions

 Mundlak Treatment: Zabel, Economics Letters, 1992

 Two step treatments: Wooldridge, 1995, etc. (See text)

 Both Fixed Effects: Greene, 2002- ‘Brute force’ (WIP)

 Random Parameters: Greene, 2003- (WIP), classical

simulation based

 Interesting survey: Jensen, Rosholm, Verner, CIM/CLS,

2002. “A Comparison of Different Estimators…”

Models for Counts

German Health Care Usage Data , 7,293 Individuals, Varying Numbers of Periods

Variables in the file are

Data downloaded from Journal of Applied Econometrics Archive. This is an unbalanced panel with 7,

individuals. They can be used for regression, count models, binary choice, ordered choice, and bivariate binary

choice. This is a large data set. There are altogether 27,326 observations. The number of observations ranges

from 1 to 7. (Frequencies are: 1=1525, 2=2158, 3=825, 4=926, 5=1051, 6=1000, 7=987). Note, the variable

NUMOBS below tells how many observations there are for each person. This variable is repeated in each row of

the data for the person. (Downlo0aded from the JAE Archive)

DOCTOR = 1(Number of doctor visits > 0)

HSAT = health satisfaction, coded 0 (low) - 10 (high)

DOCVIS = number of doctor visits in last three months

HOSPVIS = number of hospital visits in last calendar year

PUBLIC = insured in public health insurance = 1; otherwise = 0

ADDON = insured by add-on insurance = 1; otherswise = 0

HHNINC = household nominal monthly net income in German marks / 10000.

(4 observations with income=0 were dropped)

HHKIDS = children under age 16 in the household = 1; otherwise = 0

EDUC = years of schooling

AGE = age in years

MARRIED = marital status

EDUC = years of education

Hospital Visits

Histogram for Variable HOSPITAL

Frequency

HOSPITAL

0

694

1388

2082

2776

0 1 2 3 4 5 6 7 8 9 10

Choice Based Sample: Censored at Y=10, then 90% of the zeros were deleted.

Hospital Visits

+---------------------------------------------+

| Poisson Regression |

| Number of observations 4916 |

| Iterations completed 7 |

| Log likelihood function -5967.059 |

| Restricted log likelihood -5995.100 |

| Chi squared 56.08026 |

| Degrees of freedom 5 |

| Prob[ChiSqd > value] = .0000000 |

| Chi- squared = 10292.78230 RsqP= .0144 |

| G - squared = 6704.29865 RsqD= .0083 |

| Overdispersion tests: g=mu(i) : 7.283 |

| Overdispersion tests: g=mu(i)^2: 7.358 |

+---------------------------------------------+

+---------+--------------+----------------+--------+---------+----------+

|Variable | Coefficient | Standard Error |b/St.Er.|P[|Z|>z] | Mean of X|

+---------+--------------+----------------+--------+---------+----------+

Constant -.01097644 .12877669 -.085.

AGE .00492571 .00168005 2.932 .0034 44.

HHNINC .18287767 .09558999 1.913 .0557.

HHKIDS .01073511 .04023519 .267 .7896.

EDUC -.05292805 .00860326 -6.152 .0000 11.

MARRIED -.04487271 .04372825 -1.026 .3048.

Extensions of the Poisson Model

 Overdispersion

 Zero Inflation (As already discussed in class)

 Sample Selection

 Panel Data

 Endogenous RHS variables

 Semiparametric Approaches: GMM Estimators

 (The literature is vast)

Overdispersion

 In the Poisson model, Var[y|x]=E[y|x]

 Equidispersion is a strong assumption

 Negbin II: Var[y|x]=E[y|x] + σ

2

E[y|x]

2

 How does overdispersion arise:

 NonPoissonness

 Omitted Heterogeneity

j

u

1

exp( )

Prob[y=j|x,u]= , exp(x u)

j!

Prob[y=j|x]= Prob[y=j|x,u]f(u)du

exp( u)u

If f(exp(u))= (Gamma with mean 1)

Then Prob[y=j|x] is negative binomial.

α α−

∫

Testing for Overdispersion

 Regression based test: Regress (y-mean)

on

mean

 Neyman – Pearson tests in NegBin regression

| Overdispersion tests: g=mu(i) : 7.283 |

| Overdispersion tests: g=mu(i)^2: 7.358 |

Dispersion parameter for count data model

Alpha .63363306 .03061167 20.699.

Sample Selection

An approach modeled on Heckman's model

Regression Equation:

Prob[y=j|x,u]=P(λ); λ=exp(x β+θu)

Selection Equation:

d=1[z δ+ε>0] (The usual probit)

[u,ε]~n[0,0,1,1,ρ] (Var[u] is

2

absorbed in θ)

Estimation:

Nonlinear Least Squares: [Terza (1998, see cite in text).]

Φ(z δ+ρ)

E[y|x,d=1]=exp(x β+θρ )

Φ(z δ)

FIML using Hermite quadrature: [Greene (Stern wp, 97-02, 1997)]

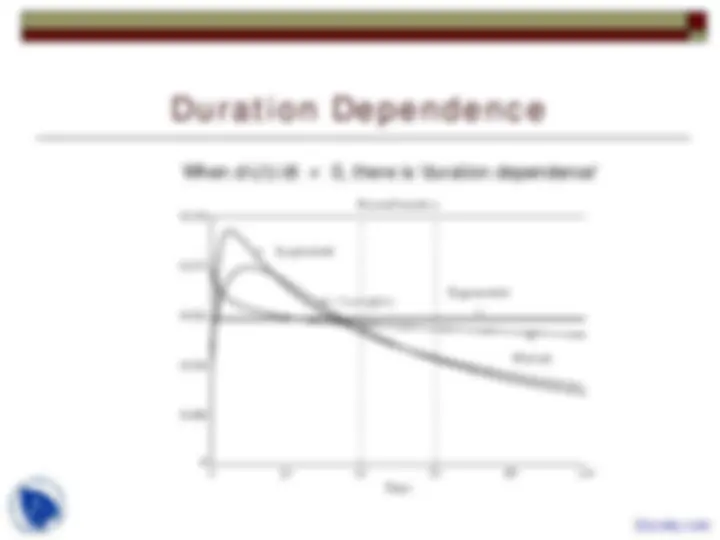
Modeling Duration

 Time until business failure

 Time until exercise of a warranty

 Length of an unemployment spell

 Length of time between children

 Time between business cycles

 Time between wars or civil insurrections

 Time between policy changes

 Etc.

Hazard Models for Duration

 Basic hazard rate model

 Parametric models

 Duration dependence

 Censoring

 Time varying covariates

 Sample selection