





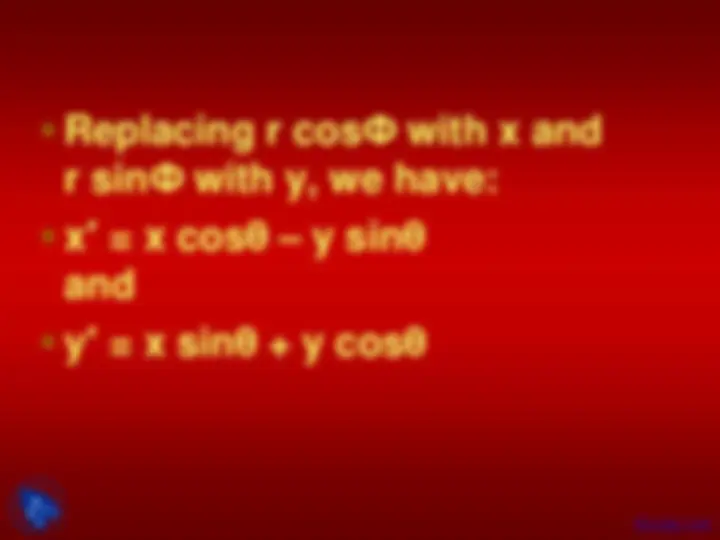
























































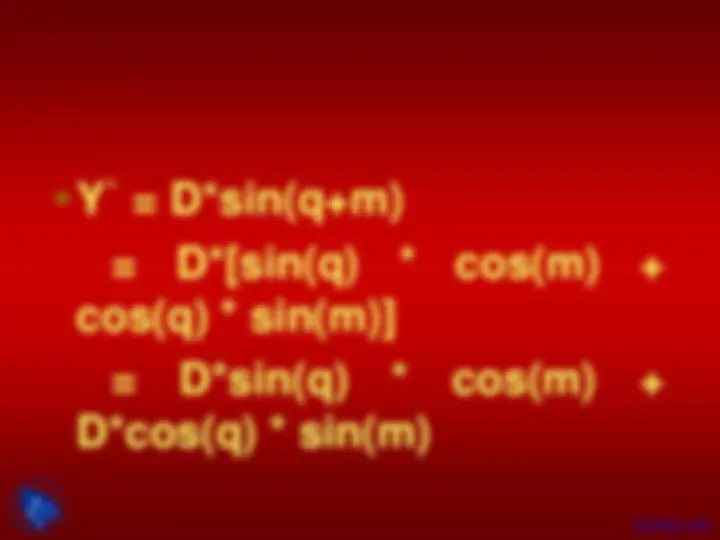













Study with the several resources on Docsity

Earn points by helping other students or get them with a premium plan


Prepare for your exams
Study with the several resources on Docsity

Earn points to download
Earn points by helping other students or get them with a premium plan
Community
Ask the community for help and clear up your study doubts
Discover the best universities in your country according to Docsity users
Free resources
Download our free guides on studying techniques, anxiety management strategies, and thesis advice from Docsity tutors
An in-depth explanation of rotation transformations in 3d computer graphics. It covers the concepts of rotation around different axes (roll, pitch, and yaw), the need for knowing rotation angles, and the mathematical formulas for rotating a point. The document also discusses the use of homogeneous coordinates for rotation representation.
Typology: Slides
1 / 85

This page cannot be seen from the preview
Don't miss anything!






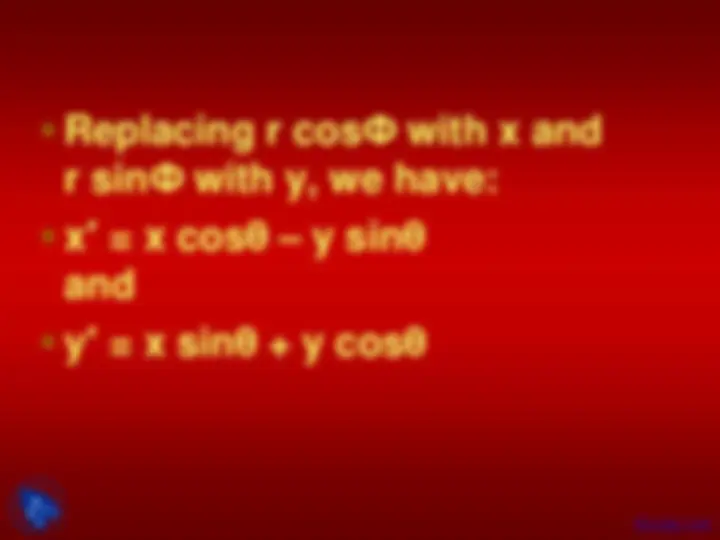




















































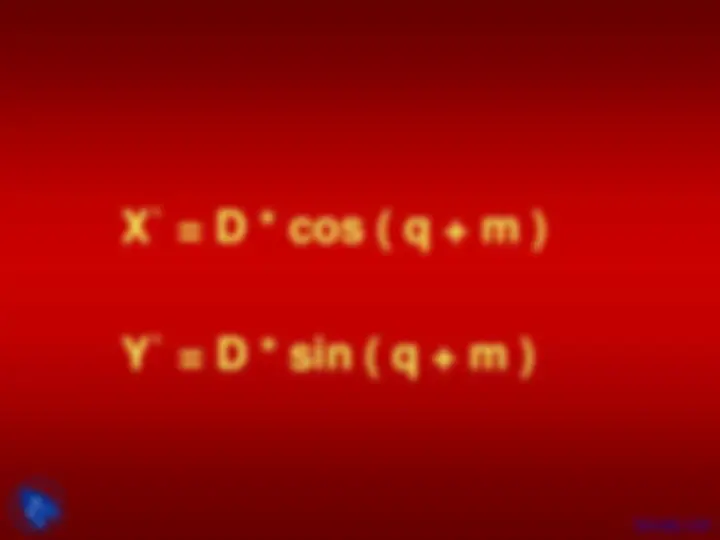






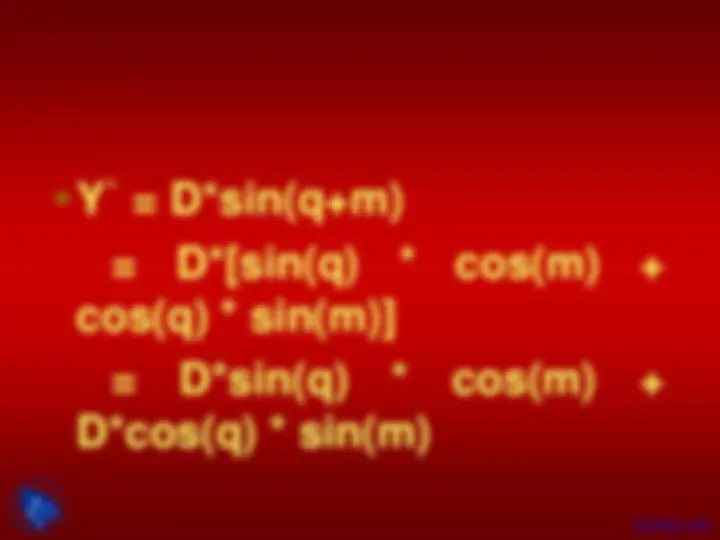











Repositions an object along a
circular path in xy-plane
Rotation Angle θ
Rotation Point (x (^) r , y (^) r )
θ is +ve counterclockwise
rotation
θ is -ve clockwise rotation
θ is zero ?
Replacing r cos Ф with x and
r sin Ф with y, we have:
x ′ = x cos θ – y sin θ
and
y ′ = x sin θ + y cos θ
Column vector representation:
P′ = R. P
Where
θ θ
θ θ sin cos
cos sin R (^)
y
x P
'
' ' y
x P
Rotation can be about any of
the three axes:
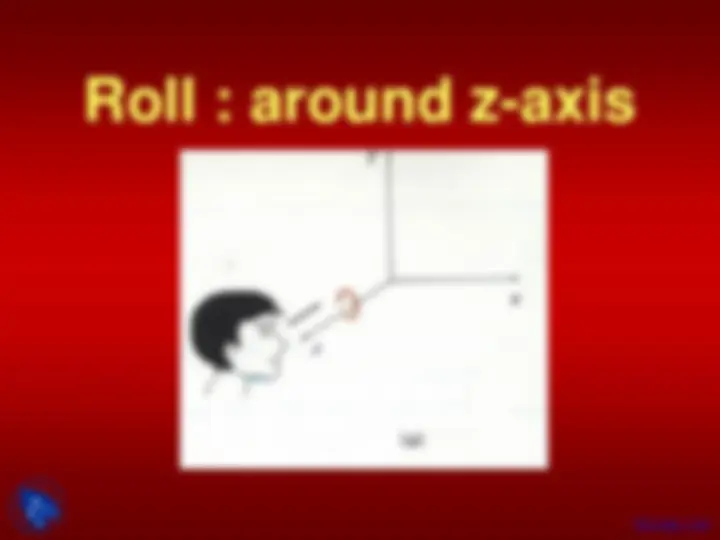
About z-axis (i.e. in xy plane)
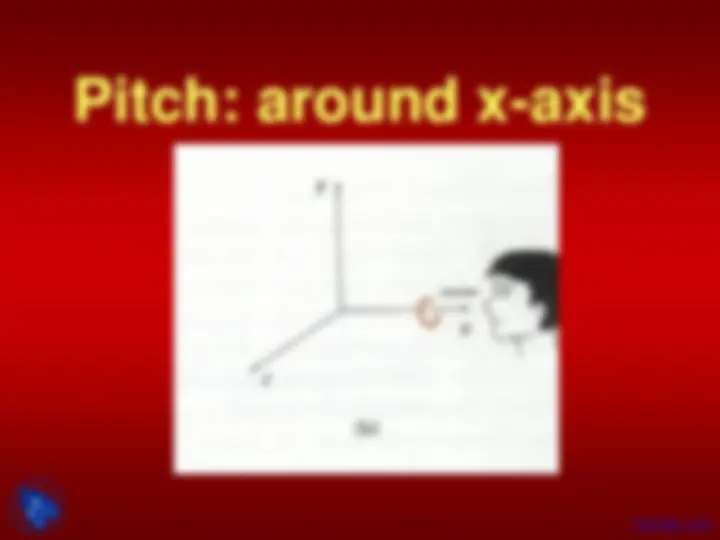
About x-axis (i.e. in yz plane)
About y-axis (i.e. in xz plane)
Cyclic Permutations of Coordinate Axes