Download Problem Set 5 For Mathematics for Management Science | MT 235 and more Assignments Mathematics in PDF only on Docsity!
MT235 Problem Set
Problem 1:
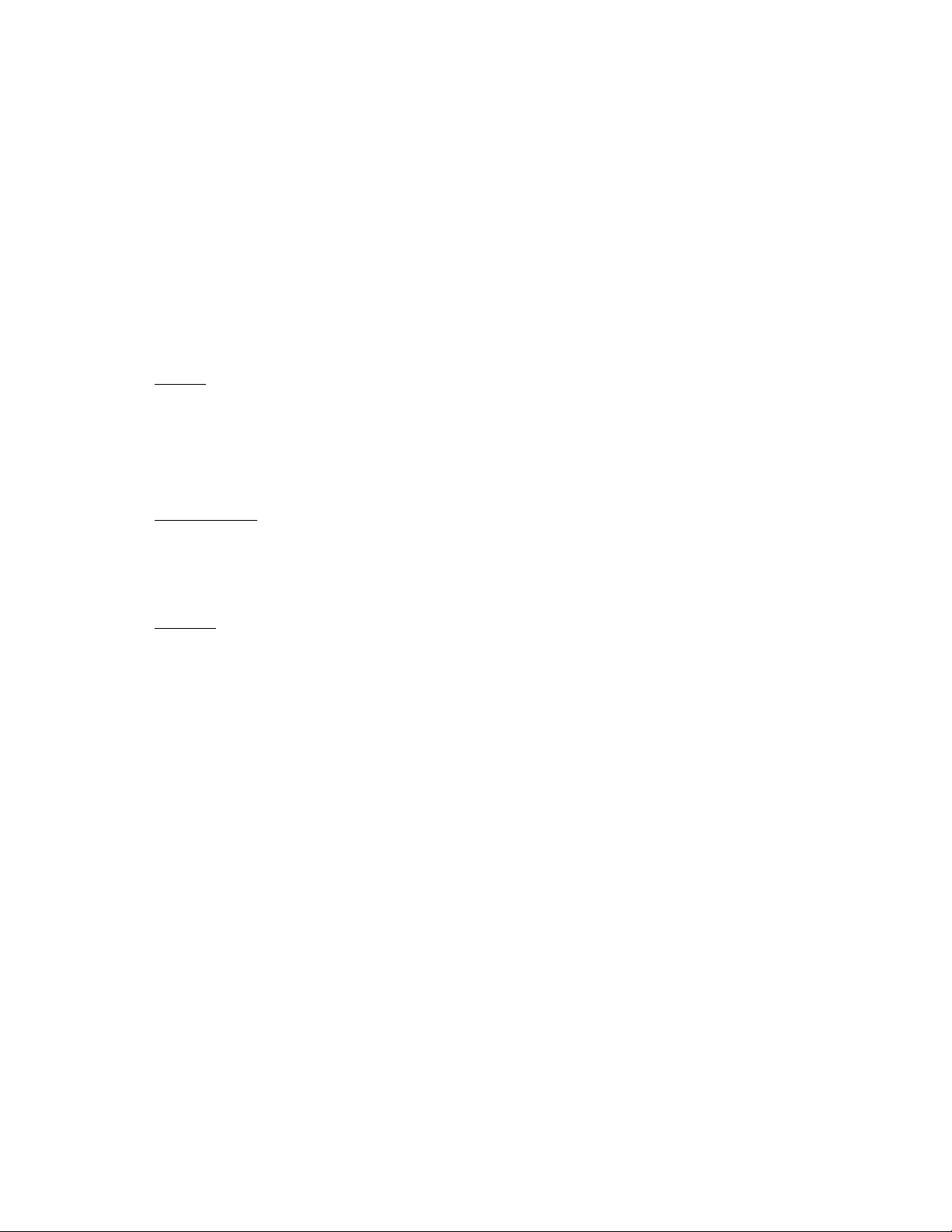
Let xij equal the number of tons of grapes shipped from node i to node j, where i and j are indexed as follows: 1 = Ohio, 2 = Pennsylvania, 3 = New York, 4 = Indiana, 5 = Georgia, 6 = Virginia, 7 = Kentucky, and 8 = Louisiana.
M in 16 x 14 + 21x 15 + 18x 24 + 16x 25 + 22x 34 + 25x 35
- 23x 46 + 15x 47 + 29x 48 + 20x 56 + 17x 57 + 24x 58
subject to the constraints:
Supply:
x 14 + x 15 = 72000 (Ohio) x 24 + x 25 = 105000 (Pennsylvania) x 34 + x 35 = 83000 (New York)
Pass-Through:
x 14 + x 24 + x 34 − x 46 − x 47 = 0 (Indiana) x 15 + x 25 + x 35 − x 56 − x 57 = 0 (Georgia)
Demand:
x 46 + x 56 ≤ 90000 (Virginia) x 47 + x 57 ≤ 80000 (Kentucky) x 48 + x 58 ≤ 120000 (Louisiana)
xij ≥ 0 ∀ i, j (Non-negativity)
See attached pages for the Excel model and Sensitivity Report. Walsh’s Fruit Company should ship 72 thousand tons of grapes from Ohio to Indiana, 105 thousand tons of grapes from Pennsylvania to Georgia, and 83 thousand tons of grapes from New York to Indiana. For the second shipment leg, they should ship 75 thousand tons of grapes from Indiana to Virginia, 80 thousand tons from Indiana to Kentucky, 15 thousand tons from Georgia to Virginia, and 90 thousand tons from Georgia to Louisiana. This shipping plan will have a minimal cost of $10,043,000.
(^2322212019181716151413121110987654321)
A B C D E F G H I J K
Walsh's Fruit Company Transshipment
Shipping Costs:
Tons
Farms
- Indiana
- Georgia
Supply
Shipped
Farms
- Indiana
- Georgia
- Ohio
72
(^0)
72
72
- Ohio
16
21
- Pennsylvania
(^0)
105
105
105
- Pennsylvania
18
16
- New York
83
(^0)
83
83
- New York
22
25
Shipped
155
105
Shipping costs:
Tons
Plants
- Virginia
- Kentucky
- Louisiana
Shipped
Plants
- Virginia
- Kentucky
- Louisiana
75
80
(^0)
155
- Indiana
23
15
29
15
(^0)
90
105
- Georgia
20
17
24
Demand
90
80
120
Shipped
90
80
90
Transshipment flows:
0 0
Cost =
10043
Distribution Centers
- Georgia 4. Indiana
Distribution Centers
Plants
Plants
- Georgia 4. Indiana
Problem 2:
Let xi equal the amount to invest in each alternative, where the potential investments are indexedas follows: 1 = Acme Chemical, 2 = DynaStar, 3 = Eagle Vision, 4 = MicroModeling, 5 = OptiPro and 6 = Sabre Systems.
M ax. 0865 x 1 +. 095 x 2 +. 10 x 3 +. 0875 x 4 +. 0925 x 5 +. 09 x 6
subject to the constraints
xi ≤ 187500 ∀ i (25% restriction) x 1 + x 2 + x 3 + x 4 + x 5 + x 6 = 750000 (Total Investment Capital) x 1 + x 2 + x 4 + x 6 ≥ 375000 (Long-Term Investments) x 2 + x 3 + x 5 ≤ 262500 (High-Risk Cap) xi ≥ 0 ∀ i (Non-Negativity)
See the attached pages for the Excel Model and Sensitivity Report. Brian Givens should invest $112,500 in Acme Chemical, $75,000 in DynaStar, $187,500 in Ea- gle Vision, $187,500 in MicroModeling, and $187,500 in Sabre Systems for a maximal return of $68887.50.
Problem 3:
Let xi be the number of workers assigned to shift i, where i is the corresponding shift number.
M in 680 x 1 + 705x 2 + 705x 3 + 705x 4 + 705x 5 + 680x 6 + 655x 7
subject to the constraints:
x 2 + x 3 + x 4 + x 5 + x 6 ≥ 18 (Sunday workers) x 3 + x 4 + x 5 + x 6 + x 7 ≥ 27 (Monday workers) x 1 + x 4 + x 5 + x 6 + x 7 ≥ 22 (Tuesday workers) x 1 + x 2 + x 5 + x 6 + x 7 ≥ 26 (Wednesday workers) x 1 + x 2 + x 3 + x 6 + x 7 ≥ 25 (Thursday workers) x 1 + x 2 + x 3 + x 4 + x 7 ≥ 21 (Friday workers) x 1 + x 2 + x 3 + x 4 + x 5 ≥ 19 (Saturday workers) xi ≥ 0 ∀ i (Non-negativity)
Problem 4
Let M 1 = the number of type 1 to manufacture, and B 1 = the number of type 1 to buy. Let M 2 = the number of type 2 to manufacture, and B 2 = the number of type 2 to buy. Let M 3 = the number of type 3 to manufacture, and B 3 = the number of type 3 to buy. Let T = the number of hours of overtime to use for wiring, and S = the number of hours of overtime to use for harnessing.
(Recall, the cost of regular time work is already factored into the components, so only the overtime premium must be added to the objective function.)
M in 50 M 1 + 61B 1 + 83M 2 + 97B 2 + 130M 3 + 145B 3 + 13T + 13S
s.t. 2 M 1 + 1. 5 M 2 + 3 M 3 − T ≤ 10000 (Wiring Hours) 1 M 1 + 2 M 2 + 1 M 3 − S ≤ 5000 (Harnessing Hours) M 1 + B 1 = 3000 (Type 1 Demand) M 2 + B 2 = 2000 (Type 2 Demand) M 3 + B 3 = 900 (Type 3 Demand) S , T , M (^) i , Bi ≥ 0 ∀i (Non-negativity)
