Download Probability and Counting - Introduction to Statistics - Lecture notes and more Study notes Statistics in PDF only on Docsity!
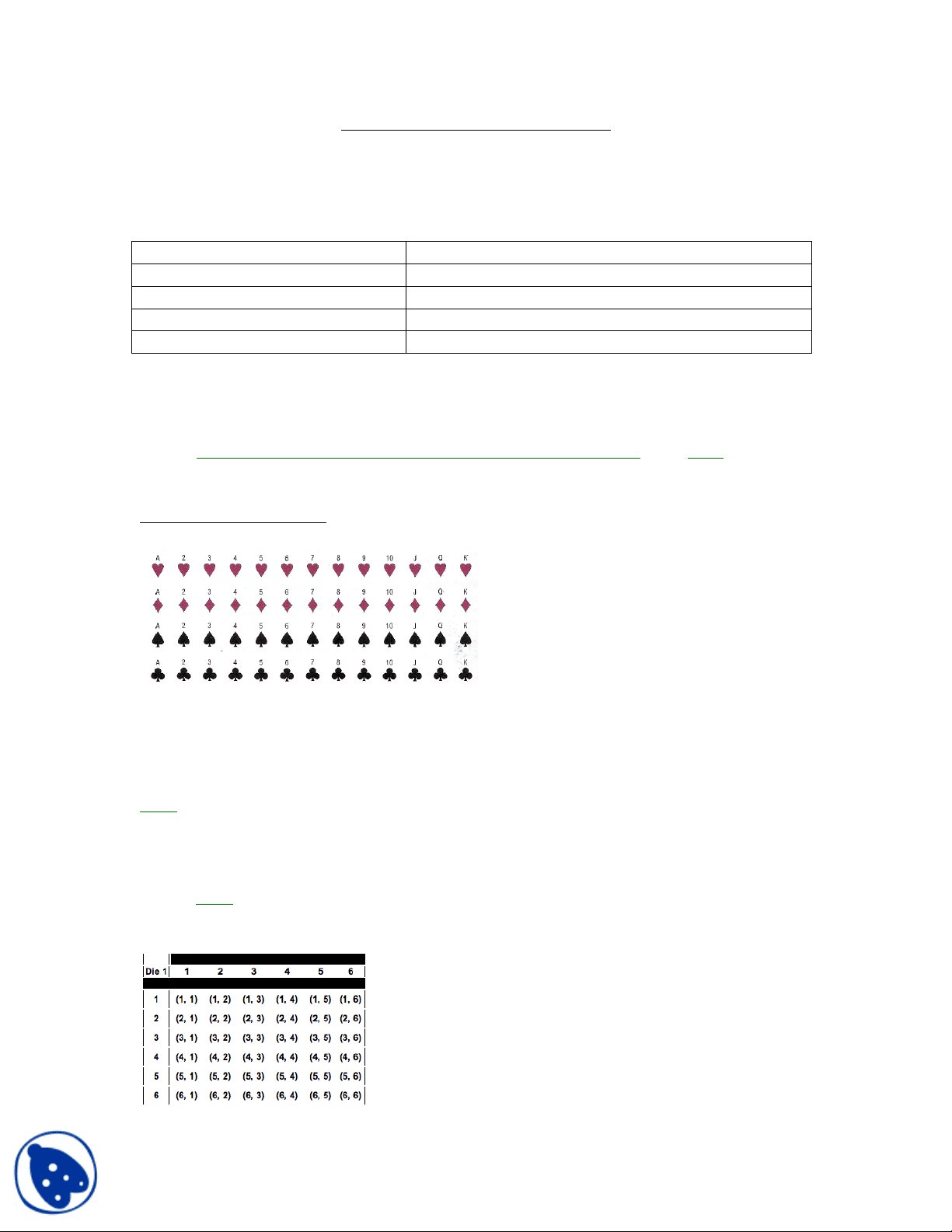
Classical & Empirical Probability A probability experiment is a chance process that leads to well-defined outcomes. A sample space is the set of all possible outcomes. Classical Probability : is applied when you can assume each event is equally likely. Experiment Sample space Coin toss Head, Tail Die roll 1, 2, 3, 4, 5, 6 True-false question True, False Double coin toss HH, HT, TH, TT An Event E is a set of outcomes Ex: flipping 2 heads in 2 tosses, rolling a 2 or a 5, etc. P(E) = Number of ways “E” can occur _ = n(E) Total number of outcomes in the sample space n(S) Classical Sample spaces: Draw a card Ex: Find the following: P(A heart) P(An ace or a two) Rule : 0 ≤ P(E) ≤ 1
- P(E) = 1 means E is a sure thing
- P(E) = 0 means E cannot occur
- Rule : Σ (probability of each event in the sample space) = 1 Ex: Roll Two Dice
P(Total value 13) = P(Total value 7) = P (A 2 and a 1) = Ex: Genetic Probablity A couple has three children, all are healthy boys or girls. P(2 girls) = P(At least 1 girl) = P(No girls) = P(All Boys) =
In a sample of 50 people, 21 had type O blood, 22 had type A blood, 5 had type B blood, and 2 had type AB blood. Set up the frequency distribution and and find the following: P(O), P(A or B), P(neither A nor O), P(not AB). Mutually Exclusive events are two events that cannot occur at the same time. Mutually Exclusive Not
- Flip a coin: E 1 = Head E 2 = Tail - Flipping 2 coins: E 1 = Two heads E 2 = At least 1 head
- Roll a die: E 1 = Rolling a 6 E 2 = Rolling a 2 - Rolling a die: E 1 = Rolling a 6 E 2 = Rolling an even #
- Draw a card: E 1 = A spade E 2 = A club - Draw a card: E 1 = A Queen E 2 = A face card Two events are independent if the outcome of the first does not affect the second. Independent: Rolling two dice (one does not affect the other) Dependent: A first and second draw from a deck (no replacement of cards).
- Notation for conditional probability: P(E 1 |E 2 )
- “The probability of E 1 given E 2 already happened”
**Rules of Probability
- Addition rules - “or”:**
- P(King or Ace) = P(king) + P (Ace) A and B mutually exclusive: P(A or B) = P(A) + P(B)
- P(king or Hart) = P(heart) + P(king) – P(King of hearts) A and B not mutually exclusive : P(A or B) = P(A) + P(B) – P(A and B) 2) Multiplication rules/Joint probability: A and B independent : P(A and B) = P(A) ⋅ P(B) Ex: Independent die rolls
- P(Six and Six) = P(Six) ⋅ P(Six) P(B) dependant on A happening: P(A and B) = P(A) ⋅ P(B|A) Ex: drawing cards without replacement
- P(Ace then King) = P(Ace) ⋅ P(King|Ace)
- Factorial! : n! = n ( n - 1)( n - 2). ⋅
- Ex: 5! = 5 ⋅ 4 ⋅ 3 ⋅ 2 ⋅ - =
So Permutations are the possible number of arrangements of objects (when order matters).
- How many ways can 5 people sit in a row?
- How many ways can 3 toothpaste brands be displayed on a shelf? How many ways can 10 people sit in 3 chairs? “10 pick 3 (with order)” or 10 P 3 10 ⋅ 9 ⋅ 8 = 10 ⋅ 9 ⋅ 8 ⋅ 7 ⋅ 6 ⋅ 5 ⋅ 4 ⋅ 3 ⋅ 2 ⋅ 1 7 ⋅ 6 ⋅ 5 ⋅ 4 ⋅ 3 ⋅ 2 ⋅ 1 =10 ⋅ 9 ⋅ 8 = 720
