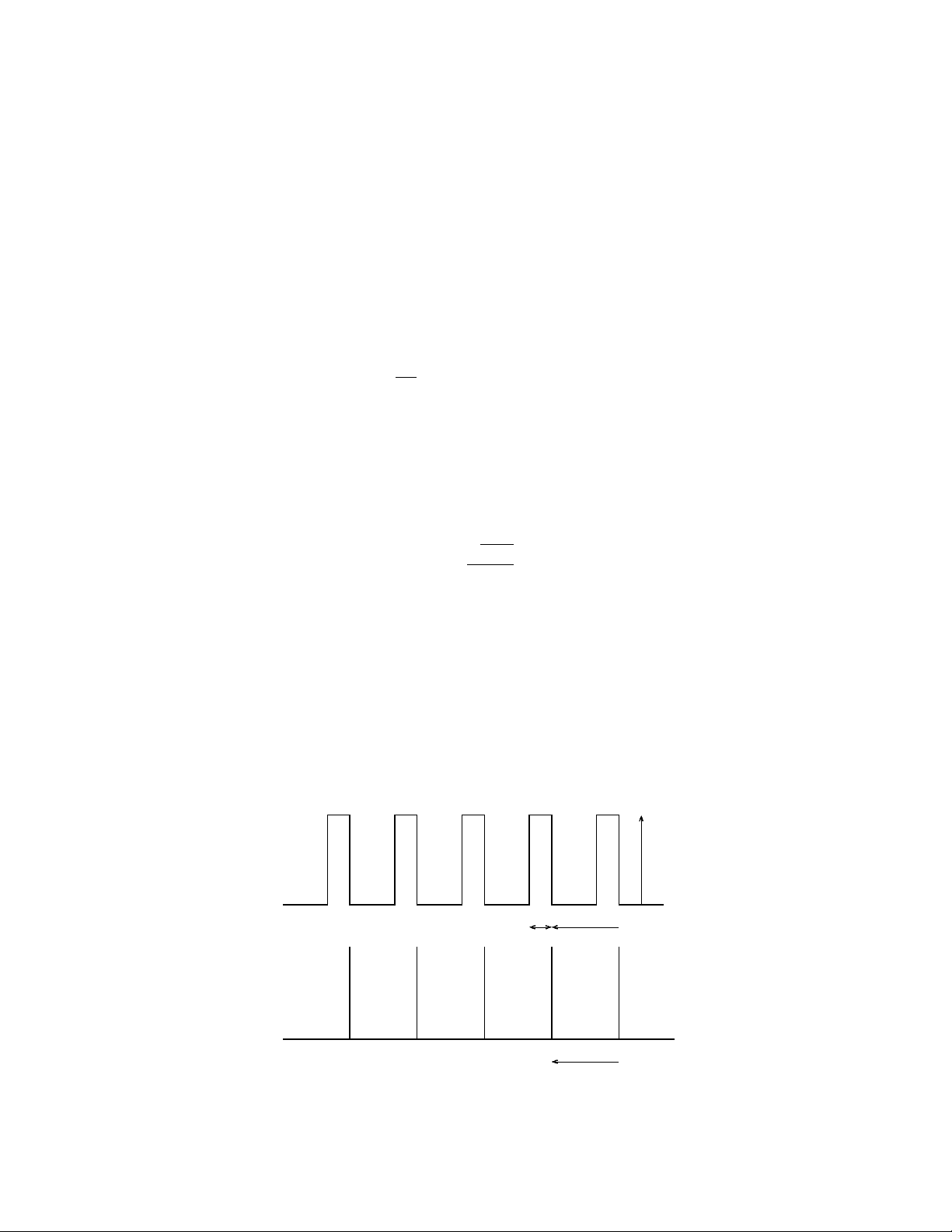





Study with the several resources on Docsity

Earn points by helping other students or get them with a premium plan


Prepare for your exams
Study with the several resources on Docsity

Earn points to download
Earn points by helping other students or get them with a premium plan
Community
Ask the community for help and clear up your study doubts
Discover the best universities in your country according to Docsity users
Free resources
Download our free guides on studying techniques, anxiety management strategies, and thesis advice from Docsity tutors
The Kronig-Penney model describes electron motion in a period array of rectangular barriers (Fig. 1, top). The Dirac-Kronig Penney model (Fig.
Typology: Study notes
1 / 5

This page cannot be seen from the preview
Don't miss anything!
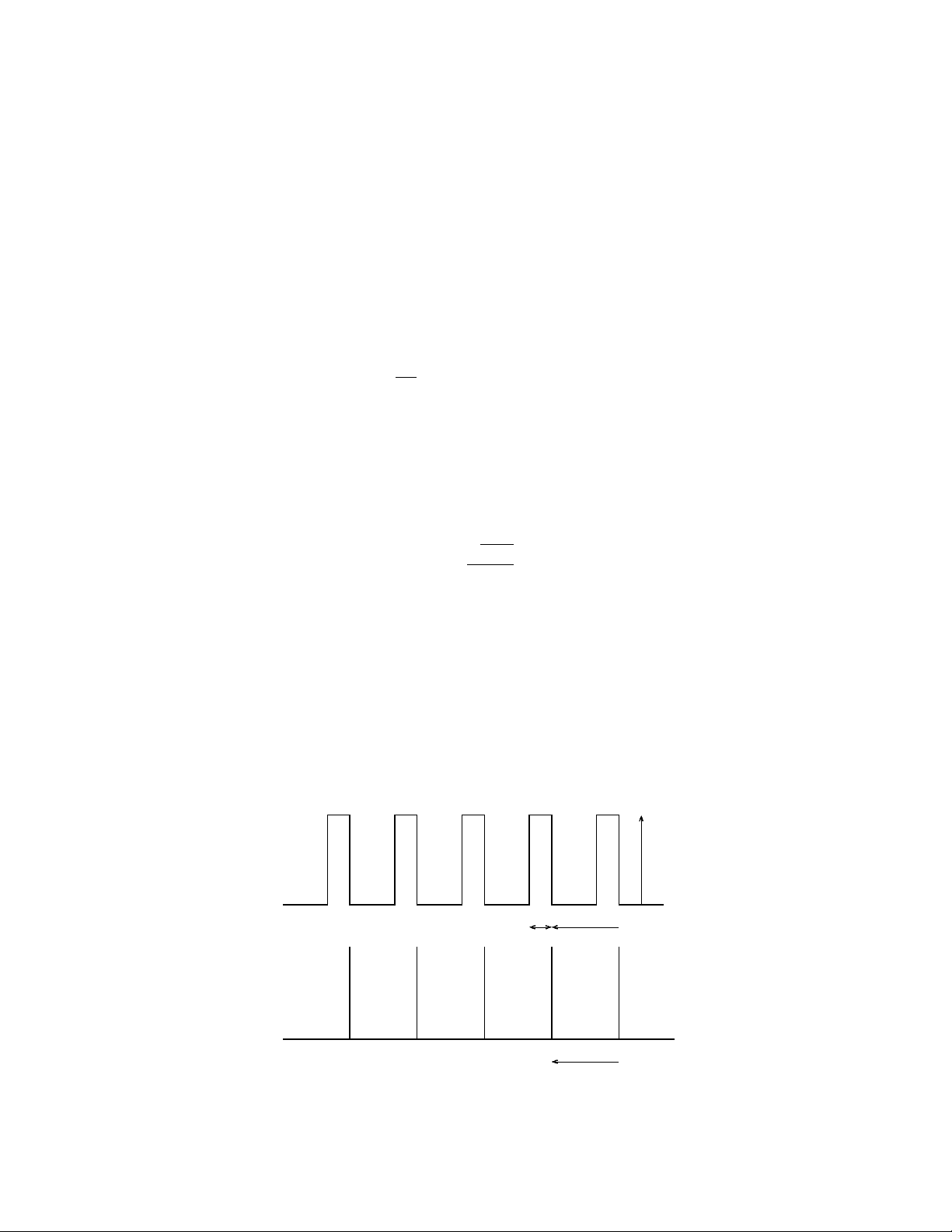



D. L. Maslov (Dated: January 25, 2012)
The Kronig-Penney model describes electron motion in a period array of rectangular barriers (Fig. 1, top). The Dirac-Kronig Penney model (Fig. 1, bottom) is a special case of the Kronig-Penney model obtained by taking the limit b → 0, V 0 → ∞ but U 0 ≡ V 0 b finite. In this limit, each of the rectangular barriers becomes a Dirac delta-function:
U (x) = U 0
n
δ (x − na).
The Schroedinger equation reads:
¯h^2 2 m
ψ′′^ (x) + U (x) ψ = Eψ.
Consider two segments: −a < x < 0 (I) and 0 < x < a (II). Since the potential energy isequal to zero inside each of the segments, the corresponding wavefunctions are the linear combinations of two plane waves
ψI (x) = Aeiqx^ + Be−iqx, ψII (x) = Ceiqx^ + De−iqx^ (0.1)
with
q ≡
2 mE ¯h
The wavefunction must satisfy the Bloch theorem
ψ(x) = eikaψ(x − a) (0.2)
If 0 ≤ x ≤ a, this implies that
ψII (x) = eikaψI (x − a)
or
Ceiqx^ + De−iqx^ = eika^
Aeiq(x−a)^ + Be−iq(x−a)
V 0
b a
a
x=
I (^) II
FIG. 1: Top: Kronig-Penney model. Bottom: Dirac-Kronig-Penney model.
Since eiqx^ and e−iqx^ are linearly independent functions, the coefficients in front of the e±iqx^ terms must match. This gives
C = Aeikae−iqa; D = Beikaeiqa,
and the wavefunction ψII becomes
ψII (x) = eika^
Aeiq(x−a)^ + Be−iq(x−a)
Boundary conditions: 1) the wavefunction is continuous at x = 0 →
A + B = eika^
Aeiqa^ + Be−iqa
and 2) a discontinuity of the wavefunction at x = 0 is obtained by integrating the Schroedinger equation over a narrow interval (−ε, ε) around x = 0
¯h^2 2 m
∫ (^) ε
−ε
ψ′′^ (x) dx + U 0
∫ (^) ε
−ε
δ (x) ψ (x) dx = E
∫ (^) ε
−ε
ψdx →
¯h^2 2 m
ψ
′ II (0)^ −^ ψ
′ I (0)
Derivatives
ψ
′ I (0)^ =^ iq^
Aiqx^ − Be−iqx
|x=0 = iq (A − B)
ψ
′ II (0)^ =^ iqe
ika
Aeiq(x−a)^ − Be−iq(x−a)
|x=0 = iqeika^
Ae−iqa^ − Beiqa
Substituting derivatives back, we obtain a 2× 2 system for A and B
1 − ei(k−q)a
1 − ei(k+q)a
ei(k−q)a^ − 1 −
2 mU 0 i¯h^2 q
−ei(k+q)a^ + 1 −
2 mU 0 i¯h^2 q
In order to have a non-trivial solution, the determinant must equal to zero→
( 1 − ei(k−q)a
−ei(k+q)a^ + 1 −
2 mU 0 i¯h^2 q
1 − ei(k+q)a
ei(k−q)a^ − 1 −
2 mU 0 i¯h^2 q
Opening brackets and simplifying yields
cos ka = cos qa +
mU 0 a ¯h^2
sin qa qa
The combination mU ¯h 20 ais a dimensionless parameter of the model ”measuring” the strength of the periodic potential.
I. GENERAL SOLUTION
Suppose that U 0 > 0. Then the maximum value of the RHS, reached at qa = 0, larger than unity
lim qa→ 0
cos(qa) + u
qa qa
= 1 + u > 0
where u ≡ mU ¯h 20 a. For larger (in absolute value) qa, the RHS decreases and oscillates. The LHS is bounded by unity: − 1 ≤ cos ka ≤ 1. Therefore, a solution in real numbers for q is possible only within those intervals where the magnitude of the RHS is less than unity. The alternation of intervals of energies corresponding to propagating states and exponentially decaying states is the characteristic feature of motion in a periodic potential.
The constant term (E′ 0 = E 0 − Jt ≈ E 0 ) can always be chosen as the origin of energy
E = 2J (1 − cos ka)
(It needs be kept in mind that, when finding the next band, the energy must be measured from E 0 ′ rather than from zero). The bandwidth, i.e., the difference between the maximal and minimal energies is equal W = 4J.
A. Properties of the spectrum
Near the bottom of the band (ka ≪ 1) , the spectrum is nearly quadratic
cos ka ≈ 1 −
(ka)^2 2 E = Ja^2 k^2
The effective mass is defined as
¯h^2 k^2 2 m∗^
= ta^2 k^2
which yields
m∗^ = m
maU 0 2 π^2 ¯h^2
≫ m
since the combination multiplying the bare electron mass is, by assumpton, much larger than unity. Therefore, electrons near the bottom of the band behave as very heavy but free particles. A similar situation occurs near the top of the band, where ka ≈ π, except for the effective mass is negative. Replacing ka = π − ε and expanding to second order in ε yields
cos ka = cos (π − ε) = − cos ε = −1 +
ε^2 2
(ka − π)^2 2
E = 4 J −
¯h^2 (k − πa)^2 2 m∗
where m∗^ is the same as before. Therefore, if the wavenumber is measured from the boundary of the Brillouin zone, the energy is a decreasing function of the wavenumber, which means that electrons behave as if the effective mass is negative.
III. SEMICLASSICAL DYNAMICS
A simple-minded derivation of the equation of motion is solids. Consider an electron in the solid subject to an external force F. The power dissipated by the force per electron must be equal to the change of the electron energy
P = vF =
dE (k) dt
∂k
dk dt
= ¯hv
dk dt
where
v =
¯h
∂k
is the group velocity. Therefore, the equation of motion is
¯h
dk dt
For a time-independent force,
k (t) = k (0) +
F t ¯h
Since E is a periodic function of k, so is v. Therefore, both the electron energy and the group velocity oscillate with time. For example, in a tight-binding model,
v =
2 Ja ¯h
sin (ka) =
2 Ja ¯h
sin
k (0) +
F t ¯h
a
1 − cos
k (0) +
F t ¯h
a
The period of oscillations is T = 2π¯h/F a. This effect is known as Bloch oscillations. The acceleration, defined, as
v˙ =
¯h
∂k^2
dk dt
¯h^2
∂k^2
m∗
where
1 m∗^
¯h^2
∂k^2
is a k dependent effective mass. The effective mass is determined by the (inverse) curvature of the energy spectrim. In a tight-bindging model,
1 m∗^
¯h^2
cos (ka)
For ka → 0 and ka → π, the effective mass approaches the limiting values determined earlier. For 0 ≤ |k| < π/ 2 a, the effective mass is positive. For π/ 2 a < k| ≤ π/a, the effective mass is negative. At the inflection point of the spectrum (k = π/ 2 a) , the effective mass is infinite. The acceleration of particles occupying states with m∗^ > 0 is along the force. The acceleration of particles occupying states with m∗^ < 0 , is opposite to the force. If the external force is electric, the acceleration contains the ratio e/m∗. Then, instead of thinking of states with negative m∗, one can flip the sign of electric charge. In this picture, the states with negative effective mass behaves as positively charged particles called ”holes”. This is how holes are introduced in many textbooks. This is an acceptable definition except for one has to keep in mind that even if the external force is not electric (and, in higher dimensions, not magnetic), the states with negative mass still have an acceleration opposite to the force. Also, if k depends on t, the effective mass oscillates in the same way as the group velocity and energy do. In the ”charge” picture, one has to say then that the effective charge oscillates in time: when a particle is below the inflection point, the charge is negative; when it is above the inflection point, the charge is positive. Either way–defining holes as particles with negative mass and negative charge or as particles with positive mass and positive charge–is fine. One should though avoid making a mistake of flipping the sign twice, i.e., treating holes as particles with negative mass AND positive charge.