Partial Differential Equations, Wave Equation-Mathematical Modeling and Simulation-Lecture Slides, Slides of Mathematical Modeling and Simulation

Download Partial Differential Equations, Wave Equation-Mathematical Modeling and Simulation-Lecture Slides and more Slides Mathematical Modeling and Simulation in PDF only on Docsity!

Mathematical Modeling

& Simulation

Partial Differential equations

Topic: Wave Equation

Some PDE Models

The 3D Wave Equation

( , ) ( , )

1 ( , ) 2

2

2

2

r t g r t t

r t

c

 



  

 



The wave equation describes propagation of waves in a

medium, with speed c.

PDE: Wave Equation

• wave equation in three dimension is:

2

2

2

2

2

2 2

2 2

z

u x y z t

y

u x y z t

x

u x y z t

t

u x y z t

u r t t

u x y z t





In two dimensional plane, it reduces to















  

  

 2

2

2

2 ( , , ) 2 ( , , ) ( , , )

y

u x y t

x

u x y t

t

u x y t 

This will be further simplified in one-dimensional wave as:

2

2 ( , ) 2 ( , )

x

u x y

t

u x y



  

 

• Let us start with detailed simulations of wave equation

One Dimensional Wave Equation

Finite Difference Method

The first step is to choose n and maxk integers.

Define step sizes h and k by

h = (b – a)/n ;

Δt = (d – c)/maxk

This means partitioning the interval (0, L) into n equal parts of width h and time interval (0, T) into maxk equal parts of width Δt.

x0 x1 x2 x3 x4 xn

0

1

2

3

m

This generates a grid.

One Dimensional Wave

Equation

Finite Difference Method

h = (L – 0)/n ;

k = (T – 0)/maxk

This means also,

1 , 2 , ,max.

1 , 2 , ,.

y c j t for all j k

x a ih for all i n

i

i





   

  

The line x = xi and t = tj are called grid lines.

Their intersections are mesh points of the grid.

Each mesh point will have the u (xi , tj ) to be computed.

0 1 2 3 4 n

0

1

2

3

m

i

j

One Dimensional Wave

Equation

4

2 4

2

2

4

2 4

2

2

2 2 2

2

x

h u

h

u i j u i j u i j

t

k u

k

u i j u i j u i j

x

u x t

t

u xi tj i j





Using above two formulas, the Poisson equation at point (xi, yj) is

For all i = 1, 2, 3,... , (n - 1); and j = 1, 2, 3,... , (m - 1)

(^00 1 2 3 4) n

1

2

3

m

i

j

One Dimensional Wave

Equation

2

2

2

h

u i j u i j u i j

k

u i j u i j u i j



Neglecting error and simplifying we get

For all i = 1, 2, 3,... , (n - 1); and j = 1, 2, 3,... , (maxk - 1)

(^00 1 2 3 4) n

1

2

3

m

i

j

where t h

u i j u i j u i j

u i j u i j u i j

2 2 2

 

  

Example 1: One Dimensional Wave Equation

Consider a problem of determining the wave distribution in a thin metal wire. The zero boundaries are along x- and y-axis and problem equation is

Analytical solution is u(x, t) = sin π x cos2πt.

( , ) 0 1 , 0 max

( , 0 ) sin ; 0 1

R x t x t t

x t

u x

u x x x

u t u t t

2

2

2

2

x L t

y

u x t

t

u x t

Subjected to following conditions:

Example 1: one-D Wave

If n = m = 4, this problem has a grid shown in the figure.

The boundary conditions and mesh points are shown here.

Red mesh points need calculations. These are nine unknowns.

MATLAB Code wave1d.m -- continued

%%%%%%%%% initialize for t = 0 and t = 1 for i=2:nx w(i,1) = sin(pix(i)); w(i,2)= (1-xlamxlam)sin(pix(i)) ...

• 0.5xlamxlam(sin(pix(i+1)) + sin(pix(i-1))); end for j=2:maxk j for i=2:nx w(i,j+1)=2.(1-xlamxlam)w(i,j)+ ... xlamxlam(w(i+1,j)+w(i-1,j))-w(i,j-1); end end % %plot(x,w(:,maxk)) % contour(x,y,u(:,:,maxk)') % This generates a sequence of 3D plots of concentration. for k=1:maxk plot(x,w(:,k)') lim =[0 1 -1 1]; axis(lim); % F(k) = getframe; k = waitforbuttonpress; end**

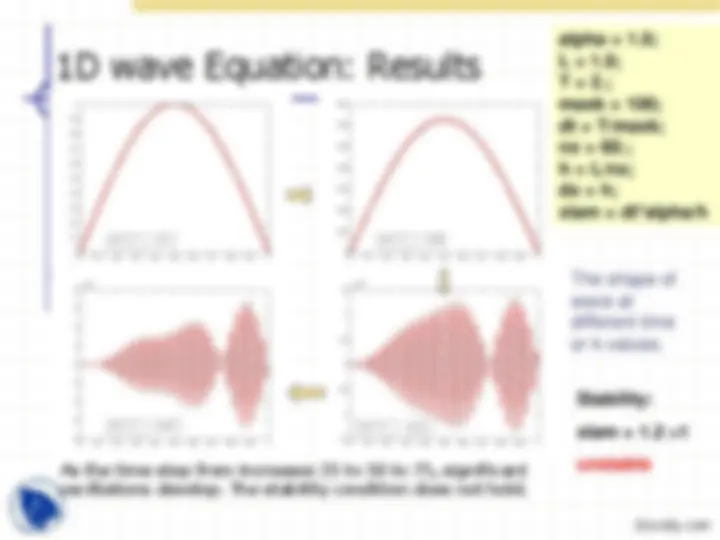
1D wave Equation: Results

alpha = 1.0; L = 1.0; T = 2.; maxk = 100; dt = T/maxk; nx = 20.; h = L/nx; dx = h; xlam = dtalpha/h*

The shape of wave at different time or k-values.

Stability:

xlam = 0.4 <

stable

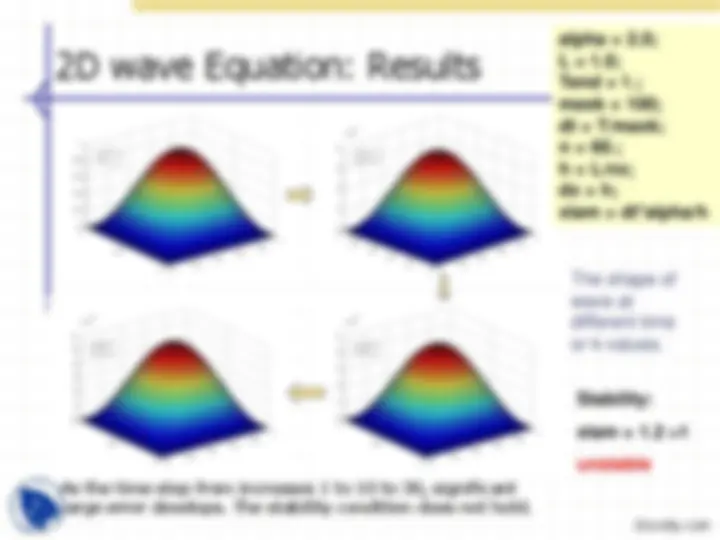
Two Dimensional Wave Equation

( , ) 0 , 0 max

R x t x L t t

g x x L t

u x

u x f x x L

u y t u L y t y W t

0 , 0 ; 0 ; 0.

( , , ) ( , , ) ( , , ) 2

2 2

2 2 2

2

    ^  

   





  

  

 x L y W t y

u x y t x

u x y t t

u x y t 

In two dimensional case, we consider the following wave equation:

It is subjected to following conditions:

Two Dimensional Wave Equation

0 , 1 , 2 , , max; , 1 , 2 , , 1.

u x y f x g y for all i j n

for all k t for all i j n

u y t u L y t u x t u x W t

i j i j

j k j k i k i k

The boundary conditions are

 

where t h

u i j k u i j k u i j k u i j k u i j k

u i j k u i j k

/

( 1 , , ) ( 1 , , ) ( , 1 , ) ( , 1 , ) ( , , 1 )

( , , 1 ) 2 ( 1 ) ( , , ) 2

2

 

        

   

For all i ,j= 1, 2, 3,... , (n - 1); and k = 1, 2, 3,... , (maxk - 1).

Δx = Δy

The finite difference form of the one-D wave equation is