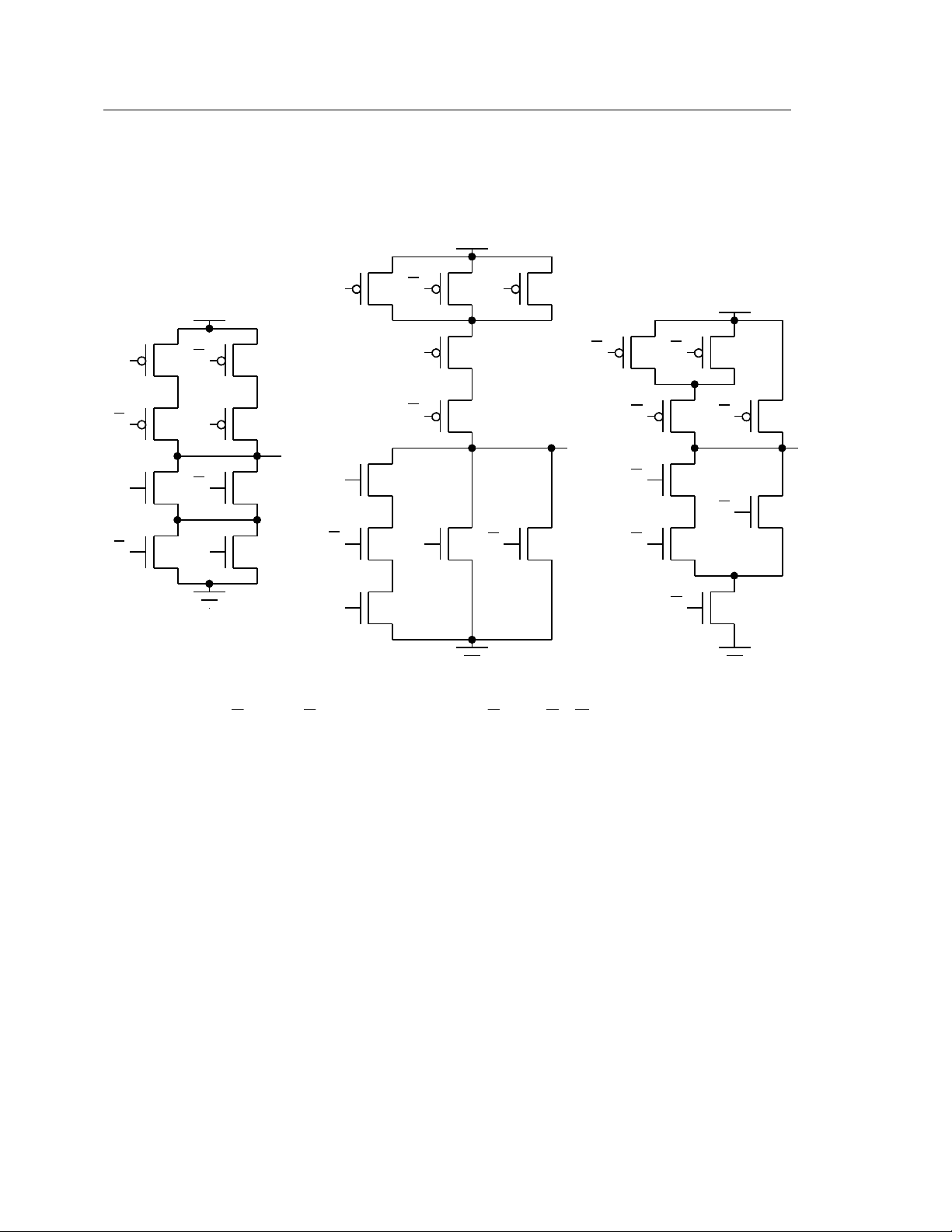




Study with the several resources on Docsity

Earn points by helping other students or get them with a premium plan


Prepare for your exams
Study with the several resources on Docsity

Earn points to download
Earn points by helping other students or get them with a premium plan
Community
Ask the community for help and clear up your study doubts
Discover the best universities in your country according to Docsity users
Free resources
Download our free guides on studying techniques, anxiety management strategies, and thesis advice from Docsity tutors
Main points of this past exam are: Output Expressions, Incomplete Circuits, Mixed Logic, Georgia Tech Engineer, Logic Notation, Mixed Logic Notation, Original Implementation, Nand Implementation, Building Blocks, Combination of Inputs
Typology: Exams
1 / 4

This page cannot be seen from the preview
Don't miss anything!
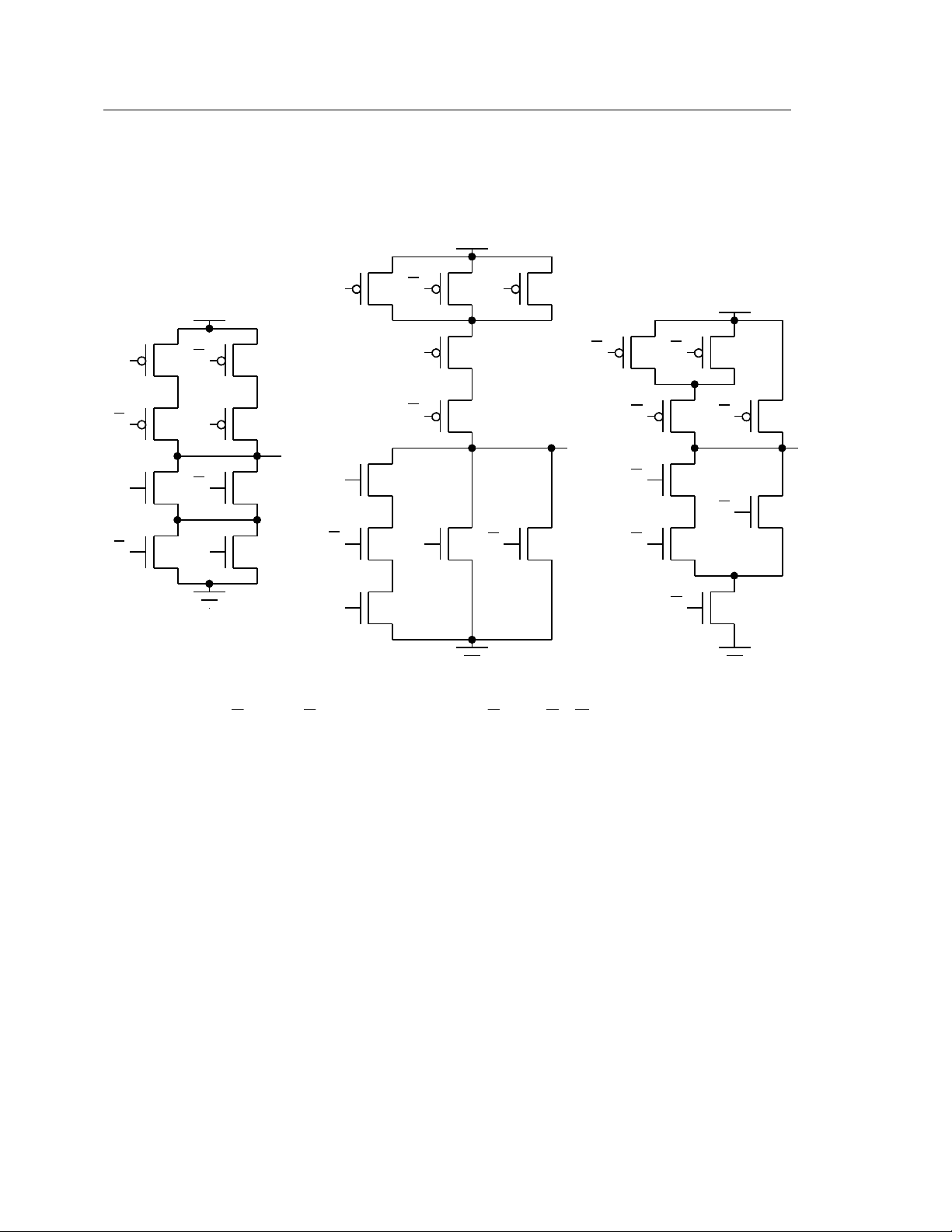


4 problems, 5 pages Exam One Solution 9 February 2001
Problem 1 (3 parts, 30 points) Incomplete Circuits For each expression below, create a switch level implementation using N and P type switches. Assume both inputs and their complements are available. Your design should contain no shorts or floats. Use as few transistors as possible, but do not simplify the expression.
A
B B
A
A B
A B
Outx
A
D
B
A
Outy
C
E
B
C
D E
B
Outz
A
D
A
B
C
C
D
OUTx = A ⋅ B + A ⋅ B OUTy = (^) ( A + (^) B + C )⋅ D ⋅ E OUTz =^ (((^ A^ + B )⋅ C )+ D )
4 problems, 5 pages Exam One Solution 9 February 2001
Problem 2 (2 parts, 25 points) Mixed Logic In the year 3000, a Georgia Tech engineer opens a millennium time capsule that contains a gate design using mixed logic notation. “Great use of a common sub-expression!” she exclaims, “But you should have used NAND gates.” Extract the two output expressions from the circuit below and then reimplement using NAND gates. Determine the transistor savings of the new design. A B C D
OUTx
OUTy F
OUTx = (^) A ⋅( B ⋅ C + D )
OUTy = (^) ( B ⋅ C + D )+ E + F
NAND gate implementation (use correct mixed logic notation) A B C D
OUTx
OUTy F
Transistors in original implementation 5 x 4 + 6 x 2 = 32
Transistors in NAND implementation 5 x 4 + 2 x 2 = 24
4 problems, 5 pages Exam One Solution 9 February 2001
Part B (10 points) For the following behavior (in map format), derive a simplified sum of products expression using a Karnaugh Map. Circle and list the prime implicants, indicating which are essential. Then write the simplified SOP expression.
prime implicants
essential? yes no
simplified SOP expression (^) A ⋅ B + B ⋅ D + A ⋅ D or A ⋅ D + A ⋅ B + B ⋅ D
Part C (10 points) For the following behavior (in map format), derive a simplified product of sums expression using a Karnaugh Map. Circle and list the prime implicants, indicating which are essential. Then write the simplified POS expression.
prime implicants
essential? yes no A + D C + D A + C
simplified POS expression (^) ( A + D )⋅( A + C )