Understanding SOP and POS Forms in Digital Logic: Notation, Computation, and Examples, Slides of Digital Systems Design

Download Understanding SOP and POS Forms in Digital Logic: Notation, Computation, and Examples and more Slides Digital Systems Design in PDF only on Docsity!

Notation

SOP and POS Forms

 SOP Given a Table of Combinations

 What is the SOP form for the following 3 input / 1

output digital device?

S A B f 0 0 0 0 0 0 1 0 0 1 0 1 0 1 1 1 1 0 0 0 1 0 1 1 1 1 0 0 1 1 1 1

 Canonical SOP

 Boolean functions can use shorthand notation when

in SOP form:

 f = S'AB' + S'AB + SA'B + SAB

f(S,A,B) = ( m 2 ,m 3 ,m 5 ,m 7 )

or

f(S,A,B) =  m (2,3,5,7)

 Canonical SOP Example

 f(x 1 ,x 2 ,x 3 ) =  m (1,4,5,6)

 f =

minterm x 1 x 2 x 3 f 0 0 0 0 0 1 0 0 1 1 2 0 1 0 0 3 0 1 1 0 4 1 0 0 1 5 1 0 1 1 6 1 1 0 1 7 1 1 1 0

x1'x2'x3 + x1x2'x3' + x1x2'x3 + x1x2x3'

 Computing the POS

 Identify rows with “0” on output (f = 0)

 Represent the input for each 0 row as a maxterm

 A logical “sum” of the input bits which guarantees that term will be “0” (sum of literals) A B f 0 0 0 0 1 1 1 0 0 1 1 0

 Canonical POS Example

 f(x 1 ,x 2 ,x 3 ) = ( M 0 , M 2 , M 3 , M 7 ) =  M (0,2,3,7)

 f =

maxterm x 1 x 2 x 3 f 0 0 0 0 0 1 0 0 1 1 2 0 1 0 0 3 0 1 1 0 4 1 0 0 1 5 1 0 1 1 6 1 1 0 1 7 1 1 1 0

(x1+x2+x3)(x1+x2'+x3)(x1+x2'+x3')(x1'+x2'+x3')

 Question:

 Under what conditions would POS form be better?

 (assuming we aren’t doing further reductions)

 Inverters in Two-Level Circuits

 Inverters are not always required for two-level logic

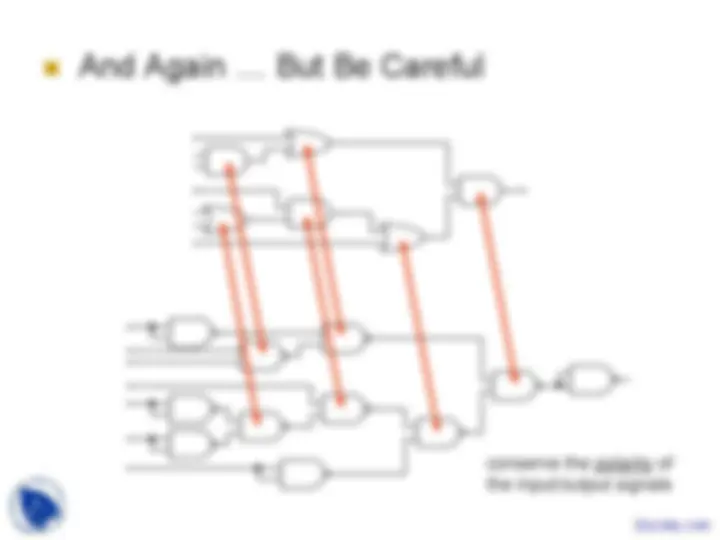
 This is why we do not always count them among the cost of a circuit

 Later, we will see that many variables will be

available to us in both normal and inverted form 

don't need to invert them

 We show them only for completeness at this point

 Completeness of NAND

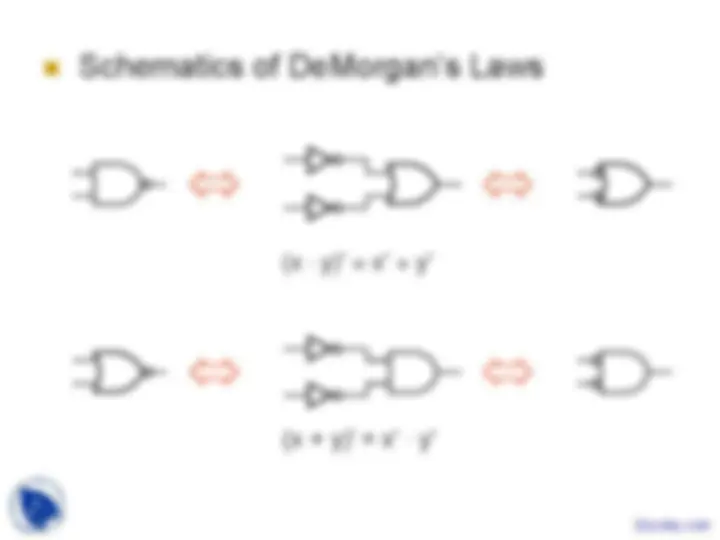
 Any Boolean function can be implemented

using just NAND gates. Why?

 Need AND, OR, and NOT

 NOT: 1-input NAND (or 2-input NAND with inputs

tied together)

 AND: NAND followed by NOT

 OR: NAND preceded by NOTs

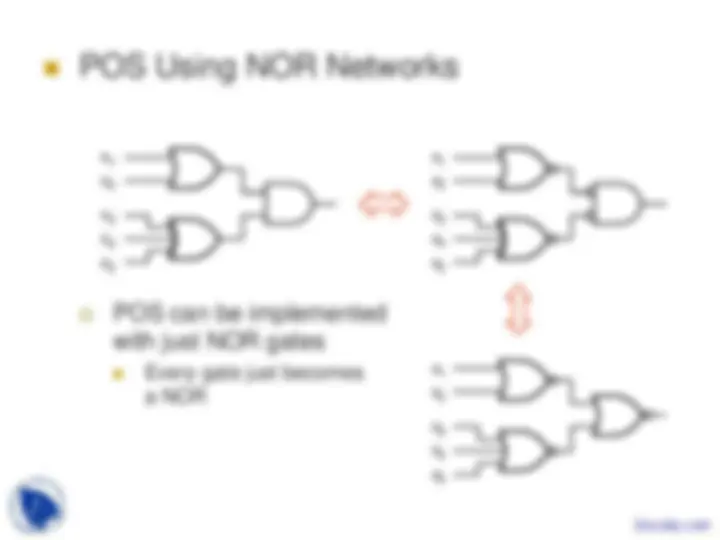
 Likewise for NOR

 Using NAND as Universal Logic

 NOT

 AND

 OR

 SOP Using NAND Networks

 SOP can be implemented

with just NAND gates

 “pushing the bubbles”  Every gate just becomes a NAND!

x 1 x 2 x 3 x 4 x 5

x 1 x 2 x 3 x 4 x 5

x 1 x 2 x 3 x 4 x 5

 2x1 MUX Using NANDs

 Implement f = S'A + SB with NAND gates only

 This one is complicated by the inverter on S!

 Schematics of DeMorgan’s Laws

(x ∙ y)' = x' + y'

(x + y)' = x' ∙ y'

 Universal Logic Families

 Any logic function can be designed using only:

 AND, OR, NOT

 NAND

 NOR

 These are called “universal logic families”

 Actual components are often designed using either

NAND or NOR gates only

 NAND and NOR require fewer transistors to build  Just having a single gate design is simpler than having 3!