More Undecidable Languages - Automata and Complexity Theory - Lecture Slides, Slides of Theory of Automata

Download More Undecidable Languages - Automata and Complexity Theory - Lecture Slides and more Slides Theory of Automata in PDF only on Docsity!

More undecidable languages

More undecidable problems

L 1 = {〈 M 〉: M is a TM that accepts input ε}

L 2 = {〈 M 〉: M is a TM that accepts some input}

L 4 = {〈 M , M’ 〉: M and M’ accept the same inputs}

L 3 = {〈 M 〉: M is a TM that accepts all inputs}

decidable recognizable but undecidable

unrecognizable

Proof by “reduction”

• Show that if L 1 can be decided,

... so can A TM

L 1 = {〈 M 〉: M is a TM that accepts input ε}

A reject if not

〈 M 〉^ accept^ if^ M^ accepts^ ε

〈 M 〉 , w reject if not

accept if M accepts w

Proof by “reduction”

〈 M 〉 , w

reject if not

accept if M accepts w

A reject if not

〈 M 〉^ accept^ if^ M^ accepts^ ε

A

〈 M’ 〉

M’ is a Turing Machine such that: If M accepts w , then M’ accepts ε If M does not accept w , then M’ does not accept ε

Recognizable or not?

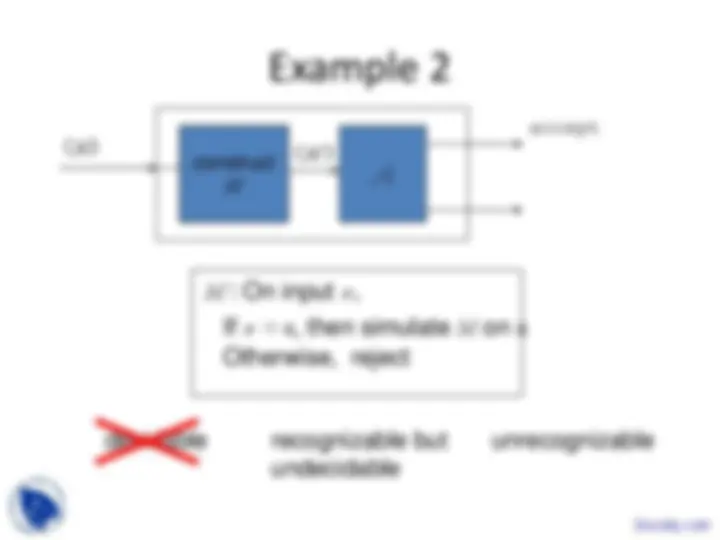
L 1 = {〈 M 〉: M is a TM that accepts input ε}

decidable recognizable but undecidable

unrecognizable

Algorithm for L 1

On input 〈 M 〉: Simulate M on input ε

Example 2

• Step 1: You gotta believe it

• To know if M accepts, it looks like we have to simulate

it

• But then we might end up in a loop

• Step 2: Use what you know

L 2 = {〈 M 〉: M is a TM that accepts some input}

A TM is undecidable L 1 is undecidable

Example 2

〈 M 〉

reject if not

accept if M accepts w A construct^ 〈 M’ 〉 M’

M’ : On input w , If w = ε, then simulate M on ε Otherwise, reject

decidable recognizable but undecidable

unrecognizable

Is it recognizable?

• Attempt to recognize L 2 :

L 2 = {〈 M 〉: M is a TM that accepts some input}

Simulate M on input ε Simulate M on input 0 Simulate M on input 1 Simulate M on input 00

Accept if one of them accepts

... but there are infinitely many!

Is it recognizable?

• Description of Turing Machine that recognizes

L 2 :

L 2 = {〈 M 〉: M is a TM that accepts some input}

For all possible strings x (in lexicographic order): For all strings y that come before x

If it accepts, accept. If it rejects, reject.

k := 1

k := k + 1

Simulate M on y for k steps

Explanation of algorithm

• Execution of algorithm

inputs ε 0 1 00 01 ...

Simulate M on ε for 1 step Simulate M on ε for 2 steps Simulate M on 0 for 2 steps Simulate M on ε for 3 steps Simulate M on 0 for 3 steps Simulate M on 1 for 3 steps

If M accepts some w , algorithm will see this in some stage of the simulation

decidable recognizable but undecidable

unrecognizable

Is it recognizable?

• Let’s try...

L 3 = {〈 M 〉: M is a TM that accepts all inputs}

Simulate M on ε for 1 step Simulate M on ε for 2 steps Simulate M on 0 for 2 steps Simulate M on ε for 3 steps Simulate M on 0 for 3 steps Simulate M on 1 for 3 steps

and then what?

accept if all of them accept but there are infinitely many!

Is it recognizable?

• To check that 〈 M 〉 is in L 3 , it looks like we have to wait for an infinite number of simulations to finish
• But we don’t have that much time!

• Step 1: You gotta believe it

... but I don’t!

L 3 = {〈 M 〉: M is a TM that accepts all inputs}

decidable recognizable but undecidable

unrecognizable

First attempt

• Let’s try...

L 3 = {〈 M 〉: M is a TM that accepts all inputs}

L 3 = {〈 M 〉: M is a TM that does not accept all inputs}

Simulate M on ε for 1 step Simulate M on ε for 2 steps Simulate M on 0 for 2 steps Simulate M on ε for 3 steps Simulate M on 0 for 3 steps Simulate M on 1 for 3 steps

accept if M rejects or loops but how to know if it loops?

How to argue unrecognizability

• Second attempt: Use what you know

• We can try to argue that

L 3 = {〈 M 〉: M is a TM that accepts all inputs}

A TM is not recognizable

If we can recognize L 3 then we can also recognize A TM