Momentum Theory - Wind Engineering - Lecture Slides, Slides of Environmental Law and Policy

Download Momentum Theory - Wind Engineering - Lecture Slides and more Slides Environmental Law and Policy in PDF only on Docsity!

Simple Performance

Prediction Methods

Module 2

Momentum Theory

Overview

• In this module, we will study the simplest

representation of the wind turbine as a disk across

which mass is conserved, momentum and energy are

lost.

• Towards this study, we will first develop some basic

1-D equations of motion.

• Streamlines
• Conservation of mass
• Conservation of momentum
• Conservation of energy

Continuity

Continuity

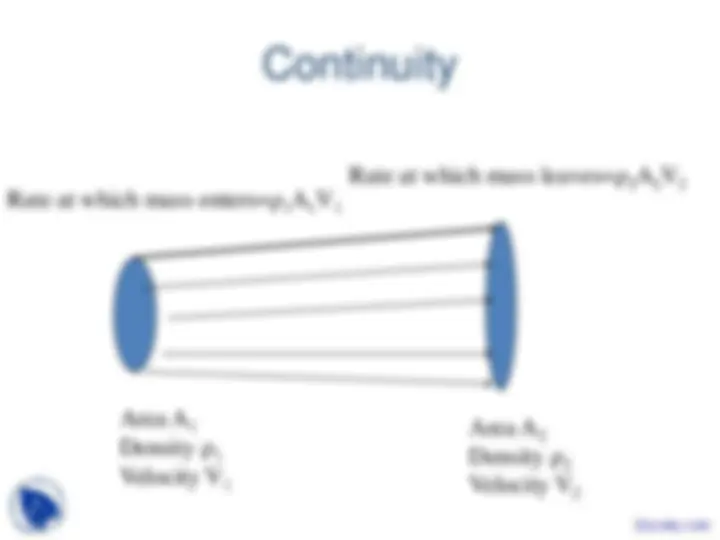
In compressible flow through a “tube”

ρAV= constant

In incompressible flow, ρ does not change. Thus,

AV = constant

Continuity (Continued..)

AV = constant

If Area between streamlines is high, the velocity is low and vice versa.

In regions where the streamlines squeeze together, velocity is high.

High Velocity

Low Velocity

Venturi Tube is a Device for Measuring Flow Rate we will study later.

Low velocity

High velocity

Momentum Equation (Contd..)

Density ρ velocity V

Area A

Density ρ+dρ velocity V+dV Area =A+dA

Momentum rate in= Mass flow rate times velocity = ρV 2 A

Momentum Rate out= Mass flow rate times velocity = ρ VA (V+dV)

Rate of change of momentum within this element = Momentum rate out - Momentum rate in = ρ VA (V+dV) - ρV 2 A = ρ VA dV

Momentum Equation (Contd..)

Density ρ

Density ρ

Velocity V

Velocity V

Area =A

Density ρ+dρ velocity V+dV Area =A+dA

Rate of change of momentum as fluid particles flow through this element= ρ VA dV

By Newton’s law, this momentum change must be caused by forces acting on this stream tube.

Forces acting on the Stream tube

Pressure times area=pA

(p+dp)(A+dA)

Horizontal Force = Pressure times area of the ring=(p+dp/2)dA

Area of this ring = dA

Net force = pA + (p+dp/2)dA-(p+dp)(A+dA)=- Adp - dp • dA/2≈-Adp

Product of two small numbers

Momentum Equation

From the previous slides,

Rate of change of momentum when fluid particles flow through the stream tube = ρAVdV

Forces acting on the stream tube = -Adp

We have neglected all other forces - viscous, gravity, electrical and magnetic forces.

Equating the two factors, we get: ρVdV+dp=

This equation is called the Euler’s Equation

Actuator Disk Theory: Background

• Developed for marine propellers by Rankine (1865),

Froude (1885).

• Used in propellers by Betz (1920)
• This theory can give a first order estimate of HAWT

performance, and the maximum power that can be

extracted from a given wind turbine at a given wind

speed.

• This theory may also be used with minor changes for

helicopter rotors, propellers, etc.

Assumptions

• Momentum theory concerns itself with the

global balance of mass, momentum, and

energy.

• It does not concern itself with details of the

flow around the blades.

• It gives a good representation of what is

happening far away from the rotor.

• This theory makes a number of simplifying

assumptions.

Control Volume

V

Disk area is A

Total area S

Station

Station 2

Station 3

Station 4

V- v (^2)

V-v (^3)

Stream tube area is A 4 Velocity is V-v (^4)

Conservation of Mass

( )

4 4

1

4 4 4

ρv A

Inflowat thetop Outflowat the bottom

Ouflowthrough theside m

Outflowthrough thebottom ρV S-A ρ(V v )A

Inflowthrough thetop ρVS

=

= −

=

= + −

=

