Download CS 150, Spring 1992 Midterm 1: Digital Logic Design and more Exams Digital Systems Design in PDF only on Docsity!
CS 150, Spring 1992
Midterm
Professor A. R. Newton
Problem #1a
Represent the following sentences by a single Boolean expression: "The tape drive motor for a computer tape drive should be running iff: (i) the tape is properly threaded, (ii) an end-of-tape signal is not present, and (iii) the tape drive is in the manual mode and the motor start button has been pressed, or it is in the automatic mode 'tape on' signal from the computer is present."
Problem #1b
Given that F = ~A~B + ~A~C + ~C~D + ~BCD (i) Use a Karnaugh map to find the maxterm representation of F. Express your answer in standard form. (ii) Use the K-map to find the minimum sum-of-products form for ~F. Express in algebraic form. (iii) Find the minimum product-of-sums for F. Express in algebraic form.
Problem #2a
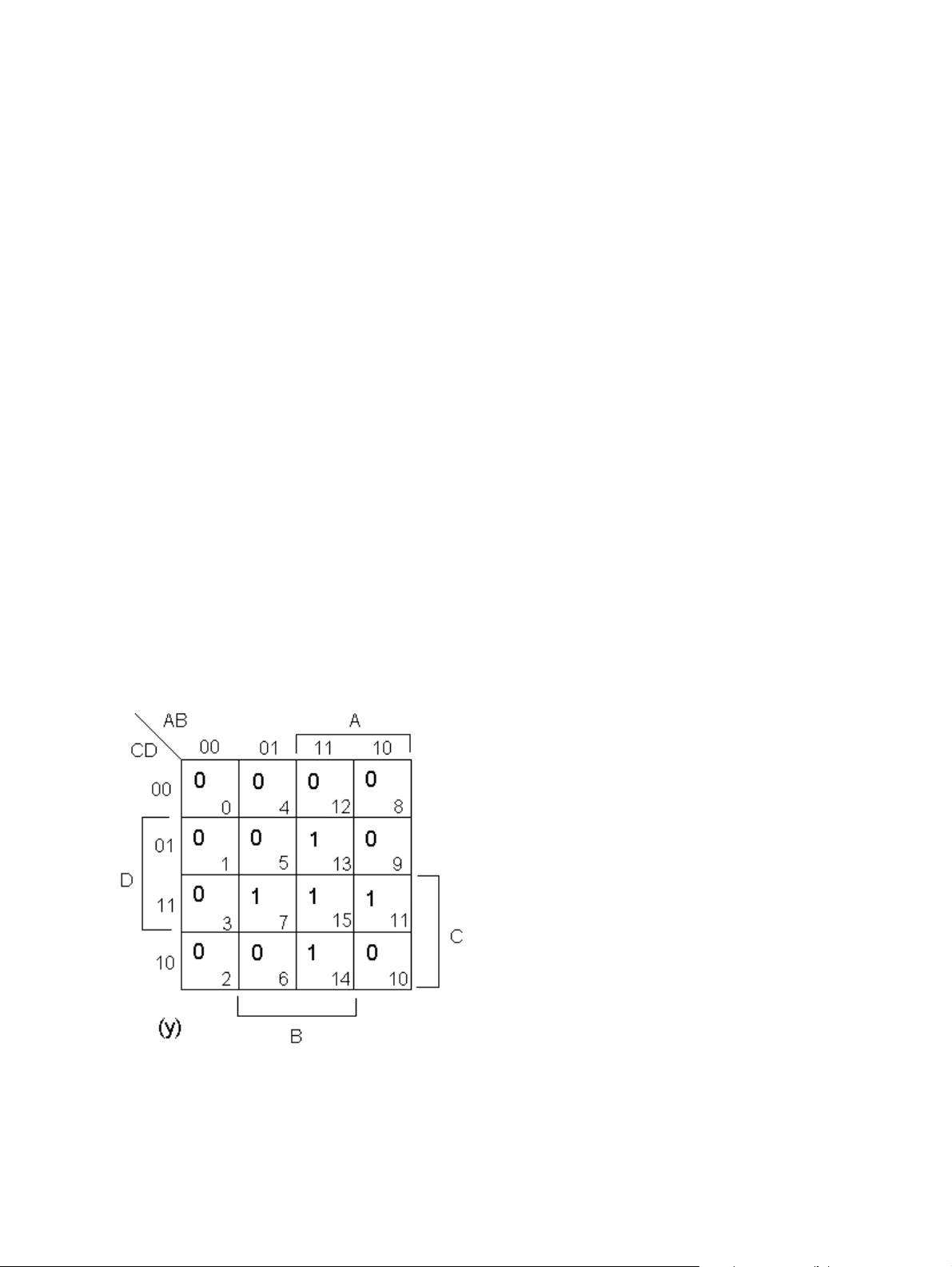
Implement the function, F, shown in the Karnaugh map below using only an 8-to-1 MUX and using A, C, and D as control inputs. Assume compliments are available.
CS 150, Spring 1992 Midterm #1 Professor A. R. Newton 1
Problem #2b
Repeat (a) above using a 4-to-1 MUX and logic gates (INV, AND, OR, NAND, NOR, XOR, or XNOR). Select the control inputs so as to minimize the number of additional gates needed. Assume compliments are available.
Problem #3a
Four people judge a competition. The vote of each is indicated by a 1 (pass) or 0 (fail) on an input wire. The four wires form the input of a logic circuit. The rules of the competition allow one dissenting vote. If the vote is 2-2 (a tie), then the competition must continue. The logic circuit is to have two outputs, x and y. If the vote is 4-0 or 3-1 to pass, then x=y=1. If the vote is 4-0 or 3-1 to fail, then x=y=0. If the vote is 2-2, then x=1 and y=0. Show Karnaugh maps for outputs x and y.
Problem #3b
Realize the logic using a minimum number of logic gates. Assume compliments are available.
Problem #4a
Consider the following schematic diagram. Develop expressions for f1, f2, and f3 as functions of A, B, and C.
Problem #4b
Develop a minimum implementation (minimum gates+gate inputs; use any type of logic gates) for f3 only. Show a schematic diagram for your minimum function.
Problem #2b 2
