



















Study with the several resources on Docsity

Earn points by helping other students or get them with a premium plan


Prepare for your exams
Study with the several resources on Docsity

Earn points to download
Earn points by helping other students or get them with a premium plan
Community
Ask the community for help and clear up your study doubts
Discover the best universities in your country according to Docsity users
Free resources
Download our free guides on studying techniques, anxiety management strategies, and thesis advice from Docsity tutors
These are the Lecture Slides of Science and Engineering of Materials which includes Point Defects, Types of Defects, Equilibrium Number, Thermal Vibrations, Boltzmann Constant, Regular Lattice Sites, Substitutional Solid Solutions, Composition Conversions etc. Key important points are: Mechanical Properties of Metals, Tension and Compression, Shear and Torsion, Stress-Strain Behavior, Elastic Deformation, Young's Modulus, Nonlinear Elastic Behavior, Potentials and Force
Typology: Slides
1 / 29

This page cannot be seen from the preview
Don't miss anything!






















Mechanical Properties of Metals How do metals respond to external loads? Stress and Strain Tension Compression Shear Torsion Elastic deformation
Plastic Deformation Yield Strength Tensile Strength Ductility Toughness Hardness
Chapter 6 Outline
Not tested: true stress-true stain relationships, resilience, details of the different types of hardness tests, variability of material properties
Introduction
Stress,
σ
(MPa)
Strain, ε (mm / mm)
Strain (For Tension and Compression)
Shear and Torsion
F is applied parallel to upper and lower faces each having area A 0.
Shear Torsion
Stress-Strain Behavior (Tension)
Elastic Plastic
Stress
Strain
Elastic deformation
Reversible:
( For small strains) Stress removed material returns to original size
Plastic deformation
Irreversible: Stress removed material does not return to original dimensions.
E = Young's modulus or modulus of elasticity (same units as σ, N/m 2 or Pa)
Gives Hooke's law for Tensile Stress
Stress
Strain
Load
Slope = modulus of elasticity E
Unload
Higher E → higher “stiffness”
Chapter 2: Potentials and Force
High modulus
Low modulus
F= (sign) dV/dr
E~ curvature of potential
at equilibrium, r (^0)
Separation, r
Weakly bonded
Strongly bonded
Force, F
Attractive is positive here
(time dependence of elastic deformation)
z
y
z
x ε
ε = − ε
ε ν = −
Theoretical value: for isotropic material: 0.
Maximum value: 0.50, Typical value: 0.24 - 0.
Zo
∆y
τ
Unloaded
Loaded
Shear stress to shear strain:
τ = G γ,
γ = tanθ = ∆y / z (^) o
G is Shear Modulus (Units: N/m 2 )
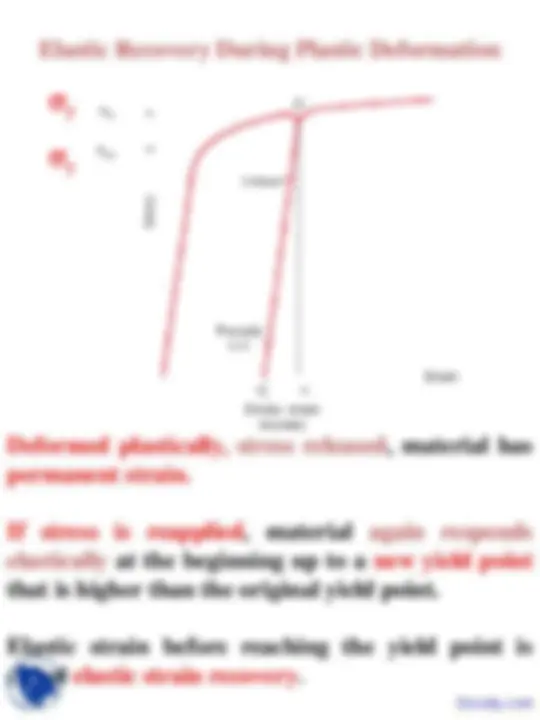
Plastic deformation (Tension)
Plastic deformation:
Elastic Plastic
Stress
Strain Yield strength: σy Permanent strain= 0.
Yield point: P Where strain deviates from being proportional to stress (the proportional limit)
A measure of resistance to plastic deformation
P
σy
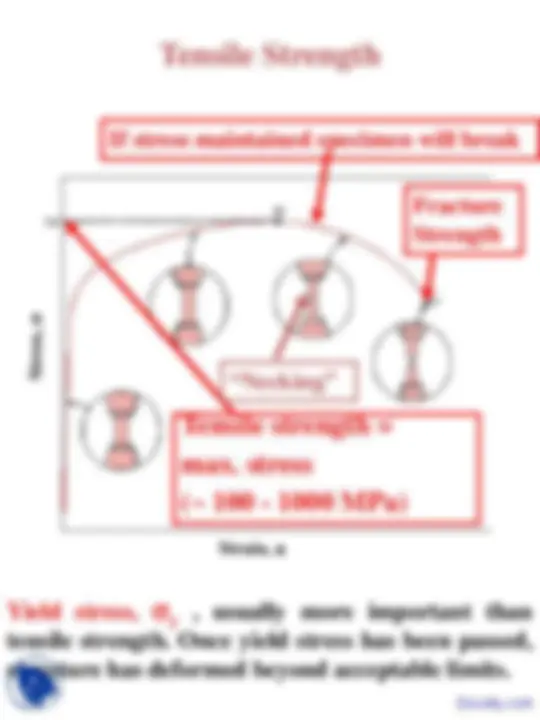
Tensile strength = max. stress (~ 100 - 1000 MPa)
If stress maintained specimen will break
Fracture Strength
Stress, “Necking”
σ
Strain, ε
Yield stress, σy , usually more important than tensile strength. Once yield stress has been passed, structure has deformed beyond acceptable limits.
percent elongation or percent reduction in area
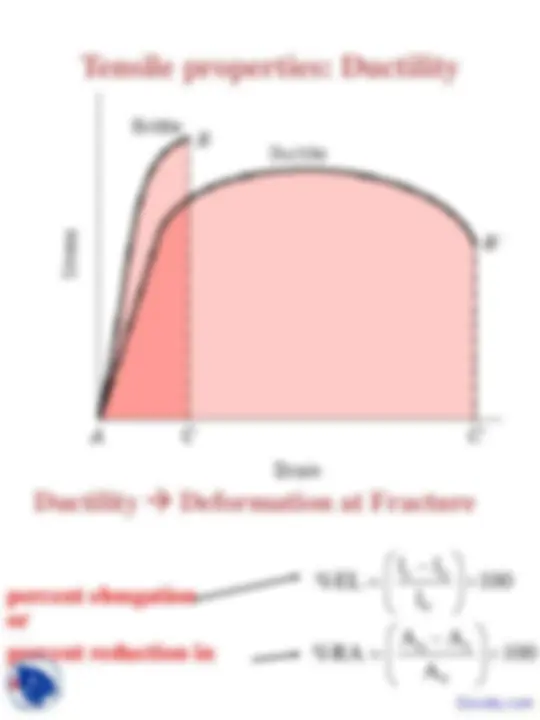
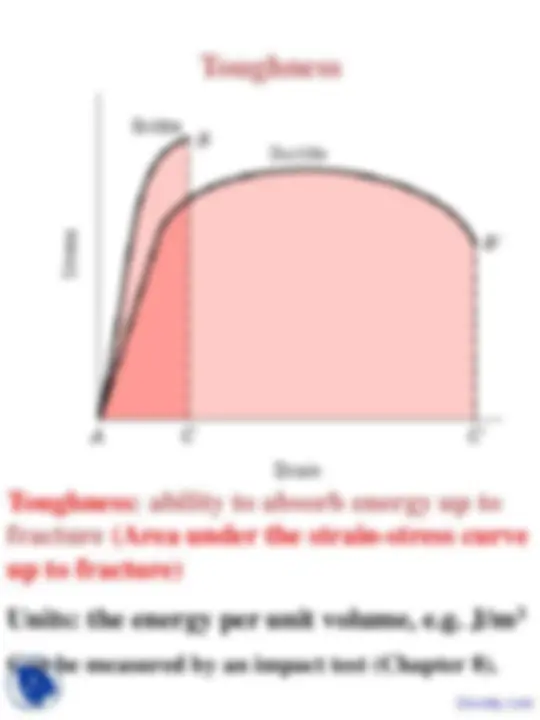
Ductility Deformation at Fracture
100 l
%EL l l 0
f (^0) ×
=^ −
100 A
%RA A A 0
0 f ×
=^ −