Linear Filter Model - Financial Econometrics - Lecture Slides, Slides of Econometrics and Mathematical Economics

Download Linear Filter Model - Financial Econometrics - Lecture Slides and more Slides Econometrics and Mathematical Economics in PDF only on Docsity!

Linear Filter Model

Linear Filter Model

 Time series in which successive values are highly dependent are regarded as generated from a series of independent shocks a (^) t.  Shock are random, drawing from fixed distribution  Normal, zero mean, variance σ a^2  the sequence of random variable at , a (^) t-1 , a (^) t-2 , …. is called white noise process

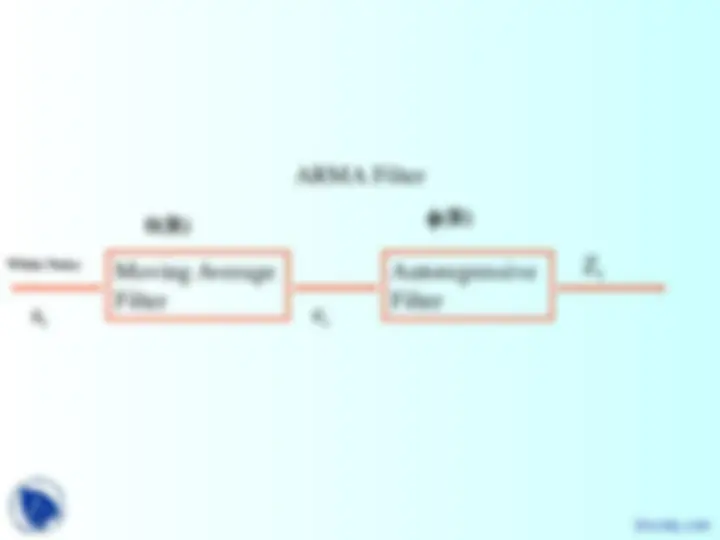
Linear Filter

White noise

a (^) t

Output z (^) t

ψ(B)

Autoregressive Models

 Stochastic Process can be represented AR(p) model  the current observation zt is a finite linear aggregate of the previous values of process and a shock.

zt = φ 1 zt-1 + φ 2 zt-2 + … + φ p zt-p + μ + a t

 If Autoregressive Operator of order p φ (B) = 1 - φ1B - φ2B 2 - …. - φpB p  φ (B) z (^) t = μ + a (^) t  Model contains p+2 unknown parameters that are μ, φ 1 , φ 2 , … φp, and σ a^2 to be estimated

AR(p) cont ….

 AR(p) process is special case of Linear Filter  Substitute z (^) t-1 = φ 1 z (^) t-2 + φ (^) 2 z (^) t-3 + … + φ pz (^) t-p-1 + μ + a (^) t into AR(p) and so on φ (B) z (^) t = μ + a (^) t  z (^) t - μ = φ (B)-1^ a (^) t  z (^) t = μ + ψ(B) a (^) t  So ψ(B) = φ (B)-

MA (q) Model Cont …

 Zt = μ + θ(B) a t

 Model contains q+2 unknown parameters that are μ, θ 1 , θ 2 , … , θq and σ a^2 to be estimated  z (^) t = μ + ψ(B) a (^) t  So ψ(B) = θ(B)

Autoregressive Moving Average

(ARMA)

 ARMA(p, q) models

 zt = μ + φ 1 zt-1 +..+ φ p zt-p+ a t – θ 1 at-1- .. - θq a t-q

φ (B) Z t = μ + θ (B ) a t

 Model contains p+q+2 unknown parameters that are μ; φ 1 , … φp; θ 1 , .. , θq;and σ a^2 to be estimated

Z t = μ + φ (B)-1 θ(B) a t

 z (^) t = μ + ψ(B) a (^) t

 So

ψ(B) = φ (B)-1 θ(B)