Languages - Automata and Complexity Theory - Lecture Slides, Slides of Theory of Automata

Download Languages - Automata and Complexity Theory - Lecture Slides and more Slides Theory of Automata in PDF only on Docsity!

1

Introduction to Finite

Automata

Languages

Deterministic Finite Automata

Representations of Automata

2

Alphabets

An

alphabet

is any finite set of

symbols.

Examples: ASCII, Unicode, {0,1} (

binary alphabet ), {a,b,c}.

4

Example: Strings

ε

Subtlety: 0 as a string, 0 as a symbol look the same.



Context determines the type.

5

Languages

A

language

is a subset of

• for some

alphabet

Example: The set of strings of 0’s and 1’s with no two consecutive 1’s.

L = {

ε

Hmm… 1 of length 0, 2 of length 1, 3, of length 2, 5 of length3, 8 of length 4.

I wonder how many of length 5?

7

The Transition Function

Takes two arguments: a state and an input symbol.

δ

(q, a) = the state that the DFA goes

to when it is in state

q

and input

a

is

received.

8

Graph Representation of DFA’s 

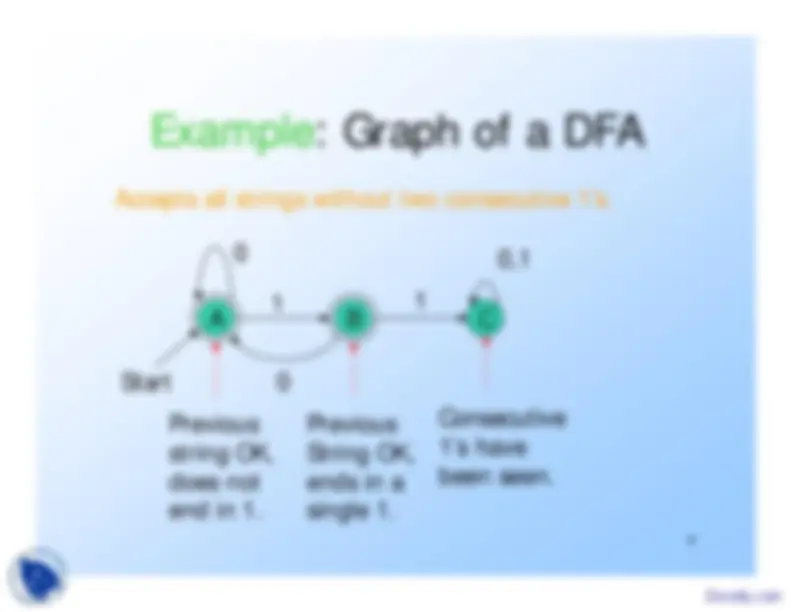
Nodes = states.

Arcs represent transition function.



Arc from state p to state q labeled by allthose input symbols that have transitionsfrom p to q.

Arrow labeled “Start” to the start state.

Final states indicated by double circles.

10

Alternative Representation:

Transition Table

0

1

A

A

B

B

A

C

C

C

C

Rows = states

Columns =input symbols

Final statesstarred

Arrow forstart state

11

Extended Transition Function

We describe the effect of a string of inputs on a DFA by extending

δ

to a

state and a string.

Induction on length of string.

Basis:

δ

(q,

ε

) = q

Induction:

δ

(q,wa) =

δ

δ

(q,w),a)



w is a string; a is an input symbol.

13

Example: Extended Delta

0

1

A

A

B

B

A

C

C

C

C

δ

(B,011) =

δ

(

δ

(B,01),1) =

δ

(

δ

(

δ

(B,0),1),1) =

δ

(

δ

(A,1),1) =

δ

(B,1) = C

14

Delta-hat

In book, the extended

δ

has a “hat” to

distinguish it from

δ

itself.

Not needed, because both agree when the string is a single symbol.

δ

(q, a) =

δ

δ

(q,

ε

), a) =

δ

(q, a)

˄

˄

Extended deltas

16

Example: String in a Language

Start

1

0

A

C

B

1

0

0,

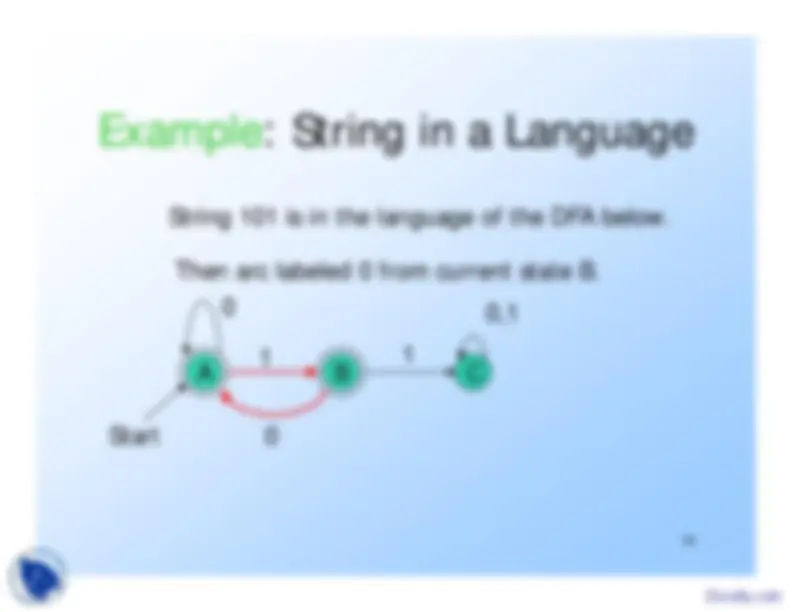
String 101 is in the language of the DFA below.Start at A.

17

Example: String in a Language

Start

1

0

A

C

B

1

0

0,

String 101 is in the language of the DFA below.Follow arc labeled 1.

19

Example: String in a Language

Start

1

0

A

C

B

1

0

0,

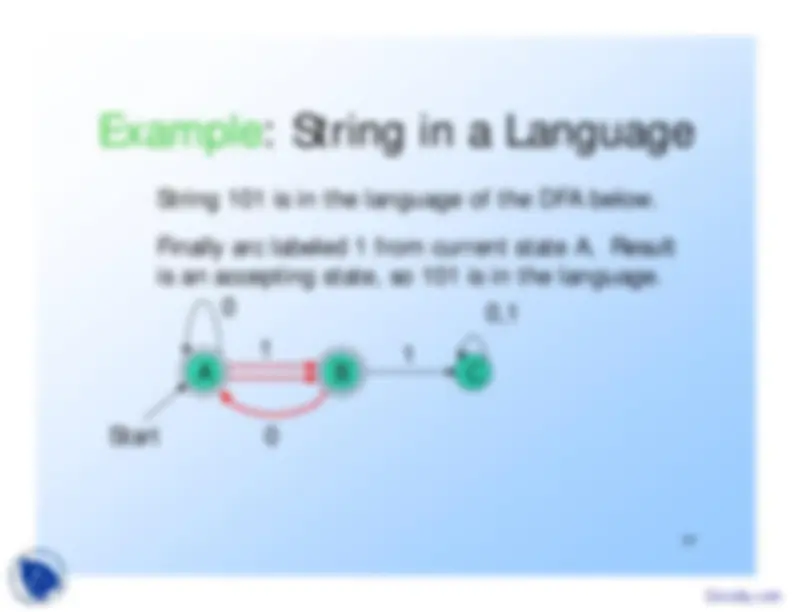
Finally arc labeled 1 from current state A.

Result

String 101 is in the language of the DFA below.is an accepting state, so 101 is in the language.

20

Example – Concluded

The language of our example DFA is:

{w | w is in {0,1}* and w does not have

two consecutive 1’s}

Read a

set former

as

“The set of strings w…

Such that…

These conditionsabout w are true.