Objectives_template
file:///G|/optical_measurement/lecture8/8_1.htm[5/7/2012 11:54:47 AM]
Module 2: Review of Probes and Transducers
lecture 8: Hot-wire anemometry
The Lecture Contains:
Hot-wire Anemometry
Prepare for your exams
Study with the several resources on Docsity
Earn points to download
Earn points by helping other students or get them with a premium plan
Guidelines and tips
Prepare for your exams
Study with the several resources on Docsity
Earn points to download
Earn points by helping other students or get them with a premium plan
Community
Ask the community
Ask the community for help and clear up your study doubts
University Rankings
Discover the best universities in your country according to Docsity users
Free resources
Our save-the-student-ebooks!
Download our free guides on studying techniques, anxiety management strategies, and thesis advice from Docsity tutors
Hot-Wire Anemometry - Optical Measurement Techniques in Thermal Sciences - Lecture Slides, Slides of Mechanical Engineering
Some concept of Optical Measurement Techniques in Thermal Sciences are Absorption Techniques, Alternative Approaches, Calibration Details, Computerized Tomography, Convolution Backprojection. Main points of this lecture are: Hotwire Measurement, Velocity Measurement, Metallic Wire, Anemometer Output, Output Voltage, Signal Conditioning, Room Temperature, Wire Fragile, Avoid Oxidization, Wire Element
Typology: Slides
2012/2013
1 / 15
This page cannot be seen from the preview
Don't miss anything!
Related documents
Partial preview of the text
Download Hot-Wire Anemometry - Optical Measurement Techniques in Thermal Sciences - Lecture Slides and more Slides Mechanical Engineering in PDF only on Docsity!
Module 2: Review of Probes and Transducers
lecture 8: Hot-wire anemometry
The Lecture Contains:
Hot-wire Anemometry
Module 2: Review of Probes and Transducers
lecture 8: Hot-wire anemometry
Review of Probes and Transducers
Hot-wire Anemometry
A hot-wire anemometer measures local instantaneous velocity based on principles of heat transfer. However, it requires that the fluid itself be at a uniform temperature. It can be used to measure three components of velocity and velocity fluctuations arising in turbulent flow. This is possible because of the high speed of response of the hot-wire probe and the associated feedback circuit. A hot-wire probe is used in gas flows, while a hot-film is used for liquid flow. The hot-wire has a limitation that it is insensitive to the flow direction. Further, it has a non-linear input-output relationship which makes its sensitivity non-uniform over any velocity range. In particular, the sensitivity decreases with increasing velocity.
The hot-wire probe is a platinum-coated tungsten wire, typically of diameter and about mm length, supported between highly conducting prongs (Figure 2.10). Tungsten has high temperature coefficient of resistance (i.e., resistance increases rapidly with temperature) and the platinum coating affords strength as well as protection against corrosion of the thin wire.
Figure 2.10: Schematic Drawing of a Hot-wire Probe.
Module 2: Review of Probes and Transducers
lecture 8: Hot-wire anemometry
Single-wire Measurement
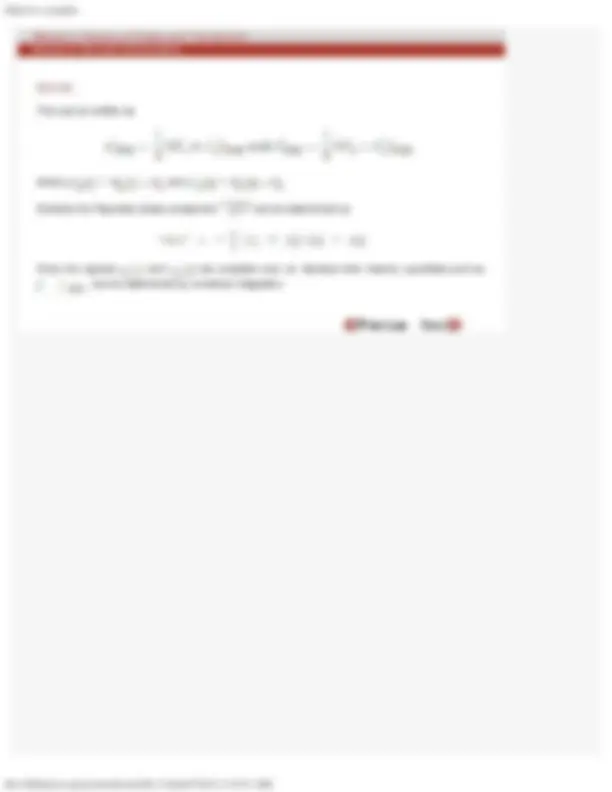
When single hot-wire probe is kept in a flow of unknown velocity it produces a voltage that can be converted into a velocity using the calibration curve. Velocity fluctuations manifest as voltage fluctuations that can be recorded as the instantaneous signal through a computer or as RMS value through a true-RMS voltmeter. If is the calibration curve, the instantaneous velocity fluctuations are determined as
where is the mean voltage corresponding to a mean velocity. The RMS value of the velocity fluctuations can be simply calculated as
Here is the derivative of the calibration curve calculated at the operating point of the probe. This formula is based on a truncated Taylor's series expansion of the function and is valid only for small values of. Experiments show that it is valid for turbulence levels upto 10 percent. For larger turbulence levels it is more accurate to construct pointwise, followed by , and and determine using numerical integration of the signal.
Module 2: Review of Probes and Transducers
Lecture 6
The hot-wire anemometer is a widely used transducer in velocity measurements and for this reason, salient features involved in its operation are discussed below:
- Wire temperature is usually in the range - C and is limited by the strength between the wire and the prongs. The corresponding wire resistances at room temperature and at are 3. and 6.5 ohms, respectively. The ratio of these resistances, called the overheat ratio is between 1. and 2.
- The hot wire output is non-zero even when^ This is because a non-zero current must flow through the wire to compensate for heat transfer to the prongs by conduction, buoyancy driven motion of the fluid around the wire and heat transfer by radiation.
- Mode of operation of the hot-wire probe described above wherein it is kept at a constant temperature results in a constant temperature anemometer (CTA). It is possible to use the probe in a constant current mode (CCA) as well. In the CCA mode the change in resistance of the wire is measured by passing a small current mA) through it and this change is related to the local velocity. It can be shown that a hot wire working in the CTA mode has a high frequency response kHz) in comparison to the CCA mode Hz). However, the CCA mode is useful in the measurement of local temperature and temperature fluctuations when the wire operates as a resistance thermometer.
Module 2: Review of Probes and Transducers
lecture 8: Hot-wire anemometry
Contd...
- Since hot-wire is based on heat transfer principles the calibration curve changes if either the wire temperature or the ambient temperature is altered. If the velocity is large ( m/s in air), heat transfer from the wire is primarily due to forced convection and hence for a given velocity the heat transfer coefficient is independent of the temperature difference. At smaller velocities additional heat transfer mechanism such as conduction to the prongs and free convection become important. When is independent of changes in can be accounted for by changing to keep and hence the calibration curve unchanged. Since the wire resistance and are related as
adjustments in can be made by a suitable setting of the operating resistance. For tungsten the value of is about C.
Module 2: Review of Probes and Transducers
Lecture 6
Two-wire Measurement
Two wires are needed for two and three wires for measuring three components of velocity respectively. Here we discuss a two-wire probe, also called a crossed wire or an X-probe (Figure 2.12).
Figure 2.12: Schematic Drawing of a X-wire Probe.
Module 2: Review of Probes and Transducers
lecture 8: Hot-wire anemometry
It is most convenient from the view point of data reduction that the functions and be close to each other, i.e. wires 1 and 2 be identical and their overheat ratios should also be equal. The measurement of and directly gives the values of and through the calibration curves. These can be related to and as follows.
For wire 1, the normal velocity component is and the longitudinal velocity component is. The heat transfer coefficient associated with each velocity component is different. Hence the effective velocity that accounts for cooling represented by the voltage is written as
where is the ratio of heat transfer coefficients in parallel flow to cross-flow past a cylinder under attached flow conditions (i.e., Re based on wire diameter. The commonly used value of is Similarly, for the second wire
Module 2: Review of Probes and Transducers
lecture 8: Hot-wire anemometry
Contd...
For the expressions for and reduce to
Extracting explicit expressions for and from these equations is difficult. However, for the limiting case of and neglecting terms of order in the binomial expansion of a square root the following relations can be derived:
Here the bar denotes the time-averaged value of the appropriate velocity component.
Module 2: Review of Probes and Transducers
lecture 8: Hot-wire anemometry
Contd...
This can be written as
where and.
Similarly the Reynolds stress component can be determined as
Once the signals and are available over an identical time interval, quantities such as can be determined by numerical integration.
Module 2: Review of Probes and Transducers
lecture 8: Hot-wire anemometry
The calculation of turbulence quantities can be greatly simplified if the two wires are identical and have the same overheat ratio. Then the wire sensitivities are also nearly equal; let be^ the representative value of the wire sensitivities and defined as
The turbulence quantities can now be obtained as