2-Hardware Design Basics of
Embedded Processors
1
Docsity.com
Prepare for your exams
Study with the several resources on Docsity
Earn points to download
Earn points by helping other students or get them with a premium plan
Guidelines and tips
Prepare for your exams
Study with the several resources on Docsity
Earn points to download
Earn points by helping other students or get them with a premium plan
Community
Ask the community
Ask the community for help and clear up your study doubts
University Rankings
Discover the best universities in your country according to Docsity users
Free resources
Our save-the-student-ebooks!
Download our free guides on studying techniques, anxiety management strategies, and thesis advice from Docsity tutors
Hardware Design - Embedded System Design - Lecture Slides, Slides of Computer Science
These are the Lecture Slides of Embedded System Design which includes Hardware Design, Elevator Controller, Simple Elevator Controller, Try Capturing, Unit Control, Request Resolver, Sequential Program Model, Partial English Description, System Interface etc. Key important points are: Hardware Design, Embedded Processors, Combinational Logic, Sequential Logic, Custom Single Purpose, Processor Design, Single Purpose Processor, Low Power, Less Flexible, Controller and Datapath
Typology: Slides
2012/2013
1 / 18
This page cannot be seen from the preview
Don't miss anything!
Related documents
Partial preview of the text
Download Hardware Design - Embedded System Design - Lecture Slides and more Slides Computer Science in PDF only on Docsity!
2-Hardware Design Basics of
Embedded Processors
Outline
• Introduction
• Combinational logic
• Sequential logic
• Custom single-purpose processor design
• RT-level custom single-purpose processor
design
CMOS transistor on silicon
• Transistor
– The basic electrical component in digital systems
– Acts as an on/off switch
– Voltage at “gate” controls whether current flows from
source to drain
– Don’t confuse this “gate” with a logic gate
source drain
oxide
gate
IC package IC
channel
Silicon substrate
gate
source
drain
Conducts if gate=
CMOS transistor implementations
- Complementary Metal Oxide
Semiconductor
- We refer to logic levels
- Typically 0 is 0V, 1 is 5V
- Two basic CMOS types
- nMOS conducts if gate=
- pMOS conducts if gate=
- Hence “complementary”
- Basic gates
- Inverter, NAND, NOR
x (^) F = x'
inverter
F = (xy)'
x
x y
y
NAND gate
F = (x+y)' x (^) y
x
y
NOR gate
gate
source
drain
nMOS
Conducts if gate=
gate
source
drain
pMOS
Conducts if gate=
Combinational logic design
A) Problem description
y is 1 if a is to 1, or b and c are 1. z is 1 if b or c is to 1, but not both, or if all are 1.
D) Minimized output equations
a
y bc
y = a + bc
00 0
1
z
z = ab + b’c + bc’
a
bc
C) Output equations
y = a'bc + ab'c' + ab'c + abc' + abc
z = a'b'c + a'bc' + ab'c + abc' + abc
B) Truth table
Inputs a b c
Outputs y z
E) Logic Gates
a b c
y
z
Combinational components
With enable input e all O’s are 0 if e=
With carry-in input Ci sum = A + B + Ci
May have status outputs carry, zero, etc.
O =
I0 if S=0.. I1 if S=0.. … I(m-1) if S=1..
O0 =1 if I=0.. O1 =1 if I=0.. … O(n-1) =1 if I=1..
sum = A+B (first n bits) carry = (n+1)’th bit of A+B
less = 1 if AB
O = A op B op determined by S.
n-bit, m x 1 Multiplexor
O
…
S
S(log m)
n
n
I(m-1) I1^ I … log n x n Decoder …
O(n-1) O1 O
I(log n -1)^ I …
n-bit Adder
n
A (^) B
n
carry sum
n-bit Comparator
n n
A B
less equal greater
n bit, m function ALU
n n
A B
…
S
n^ S(log m)
O
Sequential logic design
- Given this implementation model
- Sequential logic design quickly reduces to
combinational logic design
A) Problem Description
You want to construct a clock divider. Slow down your pre- existing clock so that you output a 1 for every four clock cycles
x=
x=0 x=
x=
a=1 a=
a=
a=
a=
a=
a=
a=
B) State Diagram
C) Implementation Model
Combinational logic
State register
a x
I
I
I
I
Q1 Q
D) State Table (Moore-type)
Inputs Q1 Q0 a
Outputs I1 I
x
Sequential logic design (cont.)
I1^ Q1Q
I1 = Q1’Q0a + Q1a’ + Q1Q0’
a 00 01 11 10
a 1
I0 Q1Q
(^0) I0 = Q0a’ + Q0’a
1
x = Q1Q
x
a
Q1Q
E) Minimized Output Equations F) Combinational Logic
a
Q1 Q
I
I
x
Greatest common divisor circuit (GCD)
- continually subtracting the smaller of the two
numbers, A or B, from the largest.
- Stop when the smallest =
- file: gcd_test_data.txt
- file: gcd_test_data_hex.txt
- State Machine?
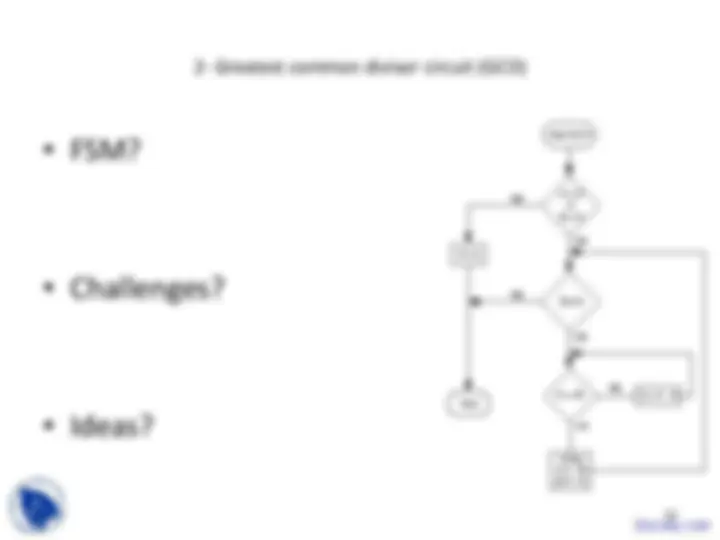
2- Greatest common divisor circuit (GCD)
- FSM?
- Challenges?
- Ideas?
Greatest common divisor circuit (GCD): Verilog module
module GCD_ALG(A_in,B_in,Y);
parameter Width = 8;
input [Width-1:0] A_in, B_in;
output [Width-1:0] Y;
reg [Width-1:0] A, B, Swap, Y;
always @(A_in)// or B) begin
begin
A = A_in; B = B_in;
if (A != 0 && B != 0)
while (B != 0) begin
while (A >= B) A = A - B;
Swap = A; A = B; B = Swap;
end
else
A = 0;
Y = A;
end
endmodule 16
Greatest common divisor circuit (GCD): Verilog module