Fluid Models First order Coupled Models-Mathematical Modeling and Simulation-Lecture Slides, Slides of Mathematical Modeling and Simulation

Download Fluid Models First order Coupled Models-Mathematical Modeling and Simulation-Lecture Slides and more Slides Mathematical Modeling and Simulation in PDF only on Docsity!

Lecture Slides

on

Modeling and Simulation

Lecture: First order Coupled Models Models : Fluid models

Sytems of Coupled ODE based Models

Most of coupled or simultaneous linear models consist of two ODEs intwo known functions y(t) and z(t) with following form:

( ) ( )

21 22

11 12 dzdt a y t a z t

dydt a y t a z t  

For example,

13 ( ) 0. 5 ( )

dzdt y t z t

dydt y t z t  

Example 1: Models for mixing of salt and two tanks

The tank Tpure water. The tank T 1 has initially 100 liters of

of water in which 150 kg of salt is^2 has 100 liters

mixed.

The liquid circulates through tanks at aconstant rate of 2 liter/minute and the

mixture is kept uniform by stirring.

Develop a mathematical model the system. What is amount of salt y 1 (t) and y 2 (t) in T 1 and T 2 tanks respectively.

T 1 T^2

Mathematical modeling: As for a single tank the time rate of change of y1(t) (amount of salt in tank-1) is equal to theinflow minus the outflow. This is also true for Tank-2:

Hence, mathematical model is a system of first order ODEs:

inflow/min -outflow/min 1002 1002 ( )

inflow/min-outflow/min 1002 1002 ( ) 2 1 2 2

1 2 1 1 y y y T

y y y T    

  

1. 02 0. 02 ( )
2. 02 0. 02 ( ) 2 1 2 2 yy^1   yy^1   yy^1 T T^1

Example 1: Models for mixing of salt and two tanks

There are two initial conditions: y 1 (0) = 0 (no salt in Tank-1); y 2 (0) = 150.

T 1 T^2

Model in MATLAB/SIMULINK

1. 02 0. 02 ( )
2. 02 0. 02 ( ) 2 1 2 2 yy^1   yy^1   yy^2 T T^1 y y

y

y y2^ y1 +0.02y -0.02y

-0.02y +0.02y To Workspace1^ y

To Workspace^ y2 Integrator1^1 s

Integrator^1 s

-0.02 Gain

0.02 Gain

0.02 Gain

-0.02 Gain

Floating Scope

Floating Scope

y y 12 (0) = 0;(0) = 150.

T 1 T^2

Example 1: Models for mixing of salt and two tanks

Model in MATLAB/SIMULINK

1. 02 0. 02 ( )
2. 02 0. 02 ( ) 2 1 2 2 yy^1   yy^1   yy^2 T T^1 y y 12 (0) = 0;(0) = 150.

T 1 T^2

(^00 20 40 60 80 ) 2040

6080

100120

140160

y1(t)

y2(t)

salt concentration time (min)

The initial salt concentrationin Tank 2 decreases from 150 exponentially andeventually saturates to 75. The concentration in tank 1grows exponentially to a saturation value of 75 withsame rate.

Example 1: Models for mixing of salt and two tanks

For a single tank the time rate of change of yequal to the inflow minus the outflow. 1 (t) (amount of salt in tank-1) is This is also true for Tank-2 and Tank-3. y 1  inflow/min - outflow/min  0. 02 y 2  0. 02 y 1 ( T 1 ) y 1  inflow/min - outflow/min  0. 02 y 1  0. 02 y 2  0. 02 y 2 ( T 2 ) y 3  inflow/min - outflow/min  0. 02 y 2 ( T 3 )

0.02y (^2) T 2 0.02y 1 0.02y 2

Mathematical modeling: Let us define y 1 (t) to be amount of salt T 1 T 3 in tank-1; y in tank-2 and tank-3 respectively. 2 (t) and y 3 (t) amount of salt

Example 2: Models for mixing of salt in three tanks

Hence, mathematical model of the mixtureproblem is a set of first order ODEs:

1. 02 ( )

2. 02 0. 04 ( )

3. 02 0. 02 ( ) 3 2 3 2 1 2 2

1 1 2 1 y y T

y y y T y y y T     

   



 

 

 

 

 

 

 

 

  

 

 

 

 



 3

2

1 3

2

1 0 0. 02 0

1. 02 0. 04 0

2. 02 0. 02 0 y

y

y y

y

y

Three initial conditions are following :y1(0) = 150 (salt in Tank-1); y2(0) = 0. ; y3(0) = 0.

0.02y (^2) T 2 0.02y 1 0.02y 2

T 1 T 3

Example 2: Models for mixing of salt in three tanks

Example 2: Models for mixing of salt in three tanks

Example 2: Models for mixing of salt in three tanks

Model in MATLAB/SIMULINK 00 .. 0202 0 (.^04 ) ( )

1. 02 0. 02 ( ) 32 12 3 2 2

1 1 2 1 yy yy T y T

y y y T   

 

Three initial conditions are following : y1(0) = 150 ; y2(0) = 0. y3(0) = 0. ;

(^00 100 200 300 400 )

50

100

150

salt concentration

time

in tank - 1 in tank - 2 in tank - 3

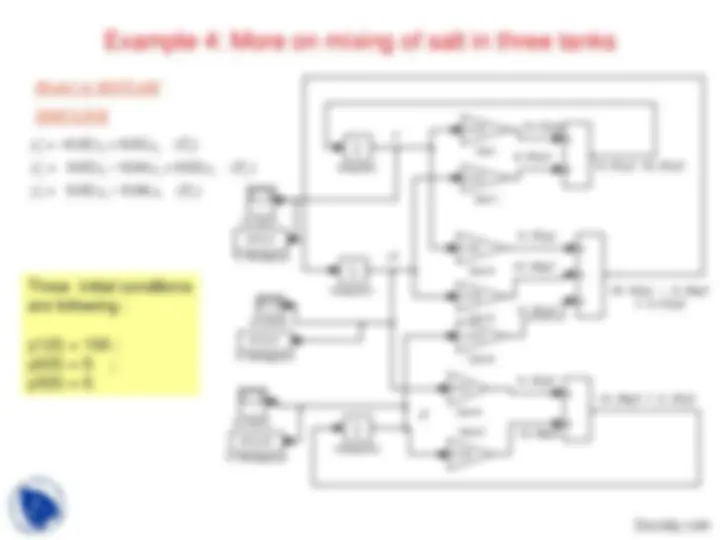
equal to the inflow minus the outflow. This is also true for Tank-2 and Tank-3.For a single tank the time rate of change of y^1 (t) (amount of salt in tank-1) is y 1  inflow/mininflow/min - -outflow/mioutflow/minn  00 .. 0202 y 2  00 .. 0202 y 1 ( 0 T. 102 ) ( ) yy 3 ^1^  inflow/min - outflow/min  0. 02 yy 21  0. 02 yy^23 ( T 3 ) y^2 T^2

0.02y (^2) T 2

0.02y 1 OUT 0.02y^2

T 1 IN T^3 OUT

IN (^) OUT IN

0.02y 3

Mathematical modeling: Let us define y in tank-2 and tank-3 respectively.^1 (t) to be amount of salt in tank-1; y^2 (t) and y^3 (t) amount of salt

Example 3: All three tanks have inflows & outflows

Hence, mathematical model is a system of first order ODEs:

1. 02 0. 02 ( )

2. 02 0. 04 0. 02 ( )

3. 02 0. 02 ( ) 3 2 3 3

2 1 2 3 2 1 1 2 1 y y y T y y y y T

y y y T   

       



 

 

 

 

 

 

 

 



  

 

 

 

 



 3

2

1 3

2

1 0 0. 02 0. 02

1. 02 0. 04 0. 02

2. 02 0. 02 0 y

y

y y

y

y

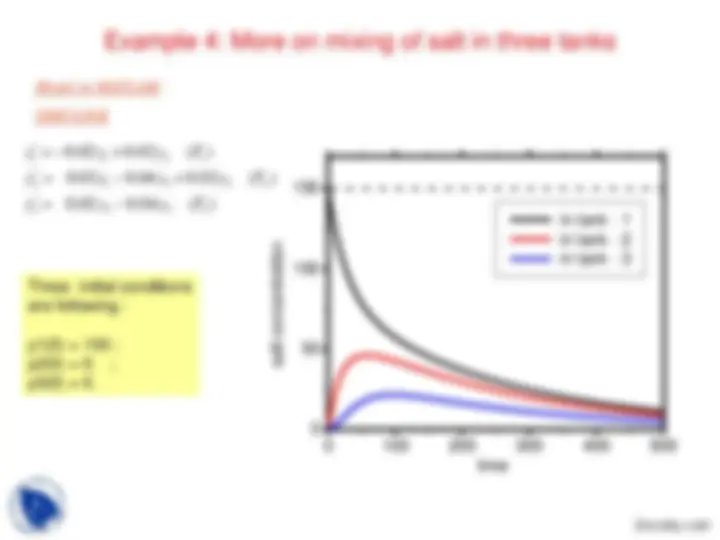
Three initial conditions are following : y 1 (0) = 150 (salt in Tank-1); yy 23 (0) = 0.(0) = 0.

Example 3: All three tanks have inflows & outflows

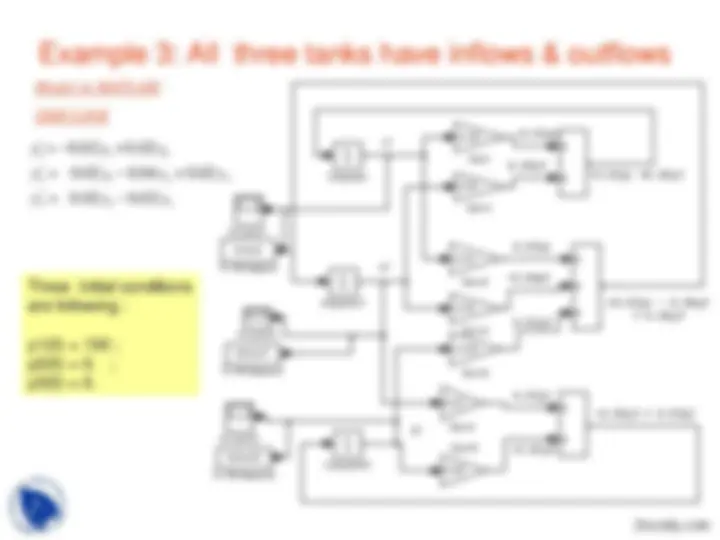
Example 3: All three tanks have inflows & outflows

32 21 23 3

1 1 2 00 .. 0202 00 ..^04020.^02

1. 02 0. 02 yy yy y y y

y y y     

 

Model in MATLAB/ SIMULINK

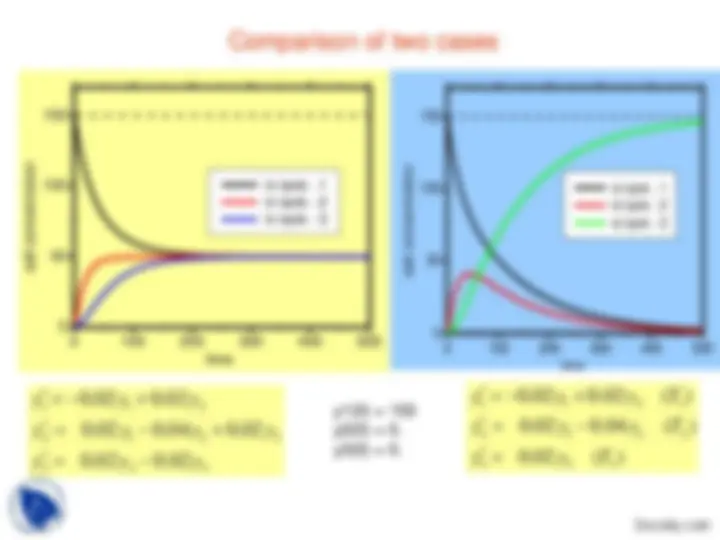
Three initial conditions are following : y1(0) = 150 ;y2(0) = 0.y3(0) = 0. ; (^00 100 200 300 400 )

50

100

150

salt concentration time

in tank - 1 in tank - 2 in tank - 3

Comparison of two cases

(^00 100 200 300 400 )

50

100

150

salt concentration time

in tank - 1 in tank - 2 in tank - 3

(^00 100 200 300 400 )

50

100

150

salt concentration time

in tank - 1 in tank - 2 in tank - 3

32 12 23 3

1 1 2 00 .. 0202 00 ..^04020.^02

1. 02 0. 02 yy yy y y y

y y y     

  00 .. 0202 0 (.^04 ) ( )

1. 02 0. 02 ( ) 32 21 3 2 2

1 1 2 1 yy yy T y T

y y y T   

y1(0) = 150 y2(0) = 0.    y3(0) = 0.