Lecture Slides
on
Modeling and Simulation
Lecture: First order Coupled Models
Models : population models
Docsity.com
Prepare for your exams
Study with the several resources on Docsity
Earn points to download
Earn points by helping other students or get them with a premium plan
Guidelines and tips
Prepare for your exams
Study with the several resources on Docsity
Earn points to download
Earn points by helping other students or get them with a premium plan
Community
Ask the community
Ask the community for help and clear up your study doubts
University Rankings
Discover the best universities in your country according to Docsity users
Free resources
Our save-the-student-ebooks!
Download our free guides on studying techniques, anxiety management strategies, and thesis advice from Docsity tutors
Lecture Slides: Modeling & Simulation of First Order Coupled Models with Lotka-Volterra, Slides of Mathematical Modeling and Simulation
Lecture slides on the topic of first order coupled models, specifically focusing on the lotka-volterra population model. The slides cover the mathematical modeling of the system, the form of the equations, and the behavior of the rabbit and fox populations. The document also includes examples of the model in matlab/simulink and the effect of simulation time on the results.
Typology: Slides
2011/2012
1 / 21
This page cannot be seen from the preview
Don't miss anything!
Related documents
Partial preview of the text
Download Lecture Slides: Modeling & Simulation of First Order Coupled Models with Lotka-Volterra and more Slides Mathematical Modeling and Simulation in PDF only on Docsity!
Lecture Slides
on
Modeling and Simulation
Lecture: First order Coupled Models
Models : population models
Sytems of Coupled ODE based Models
Most of coupled or simultaneous linear models consist of two ODEs in
two known functions y(t) and z(t) with following form:
21 22
11 12
a y t a z t dt
dz
a y t a z t dt
dy
For example,
y t z t dt
dz
y t z t dt
dy
Lotka – Volterra Population Model
This model involves two species, say rabbits and foxes. Foxes prey on
rabbits and we assume the following:
- Rabbits have unlimited food supply. Hence, if there were no foxes their
number r(t) would increase exponentially. That means their rate of
change is proportional to their number when there are not any foxes.
- However, actually, r(t) decreases as rabbits are killed by foxes say at
rate proportional to -r(t)f(t) where f(t) is number of foxes.
- If there were no rabbits the foxes would decrease exponentially to zero,
which means their rate of change is proportional to – f(t) when there are
no rabbits.
- When rabbits are there then the rate of change is also proportional to
+r(t)f(t).
Mathematical modeling:
production rater(t)
Lotka – Volterra Population Model
ar brf dt
dr
Rabbits have unlimited food supply. Hence, if there were no foxes, the rabbits ‘s
number r(t) would increase exponentially. That means their rate of change is
proportional to their number when there are not foxes.
First consider rabbits to see rate of change of r(t).
However, actually, r(t) decreases as rabbits are killed by foxes say at rate proportional
to -r(t)f(t) where f is number of foxes.
loss rater(t)
Net rate of change = production rate – loss rate
production ratear(t)
loss ratebr(t)
Mathematical model for rabbit population
Mathematical modeling:
For rabbits we see rate of change of r(t) is
ar brf dt
dr
For foxes we see rate of change of f(t) is
cf drf dt
df
cf drf foxes
dt
df
ar brf rabbits
dt
dr
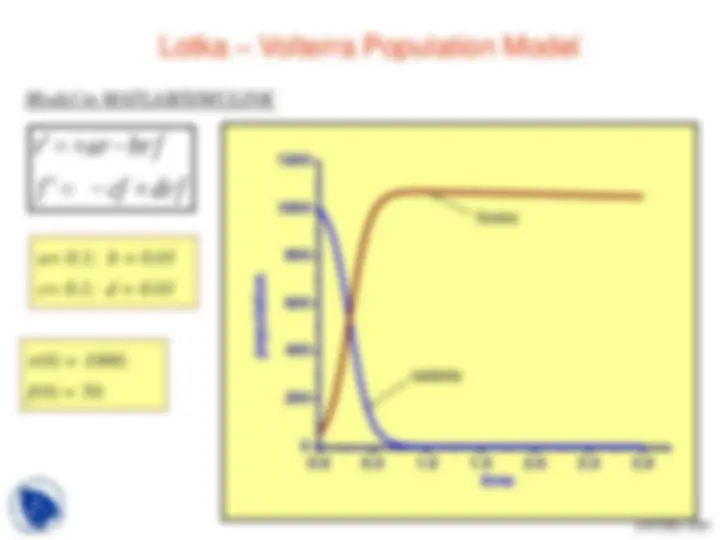
Let us consider a real example, with following two equations
Let us assume Initial conditions as : r(0) = 1000; f(0) =
This model is a Nonlinear first order Homogeneous, ODE Based model
Lotka – Volterra Population Model
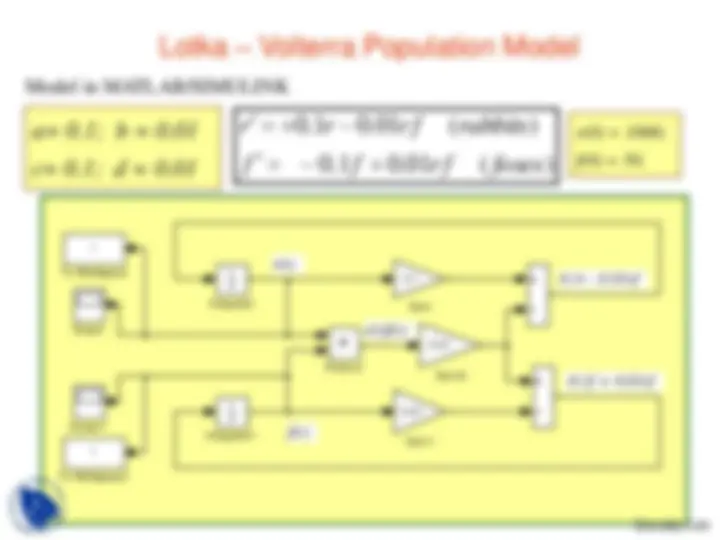
Model in MATLAB/SIMULINK
r(0) = 1000;
f(0) = 50.
Lotka – Volterra Population Model
1 0. 01 ( )
1 0. 01 ( )
f f rf foxes
r r rf rabbits
r(t)
f(t)
r(t)f(t)
0.1r - 0.01rf
-0.1f + 0.01rf
f
To Workspace
r
To Workspace
Scope
Scope
Product
1 s Integrator
1 s Integrator
Gain
Gain
Gain
a= 0.1; b = 0.
c= 0.1; d = 0.
Model in MATLAB/SIMULINK
r(0) = 1000;
f(0) = 50.
Lotka – Volterra Population Model
( )
( )
f cf drf foxes
r ar brf rabbits
a= 2.0; b = 0.01
c= 10; d = 0.
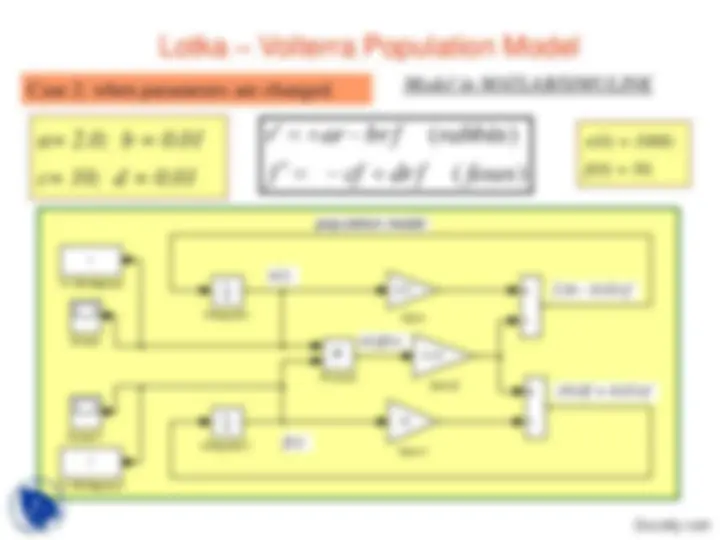
Case 2: when parameters are changed.
r(t)
f(t)
r(t)f(t)
2.0r - 0.01rf
-10.0f + 0.01rf
population model
f To Workspace
r To Workspace
Scope
Scope
Product
1 s Integrator
1 s Integrator
Gain
10
Gain
Gain
Model in MATLAB/SIMULINK
Initial cond.
r(0) = 1000;
f(0) = 50.
Lotka – Volterra Population Model
f cf drf
r ar brf
a= 2.0; b = 0.
c= 10.0; d = 0.
0.0 0.5 1.0 1.5 2.0 2.5 3.
0
200
400
600
800
1000
1200
1400
1600
1800
rabbits
foxes
population
time
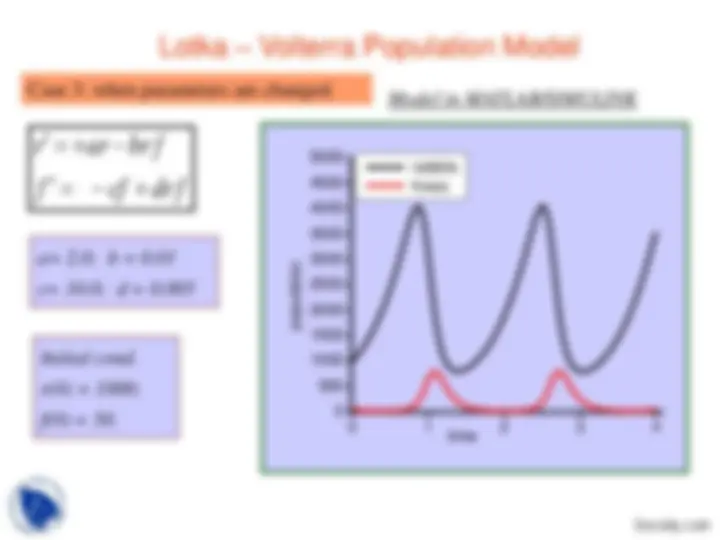
Case 2: when parameters are changed.
Model in MATLAB/SIMULINK
Initial cond.
r(0) = 1000;
f(0) = 50.
Lotka – Volterra Population Model
f cf drf
r ar brf
a= 2.0; b = 0.
c= 10.0; d = 0.
Case 3: when parameters are changed.
0 1 2 3 4
0
500
1000
1500
2000
2500
3000
3500
4000
4500
5000
population
time
rabbits foxes
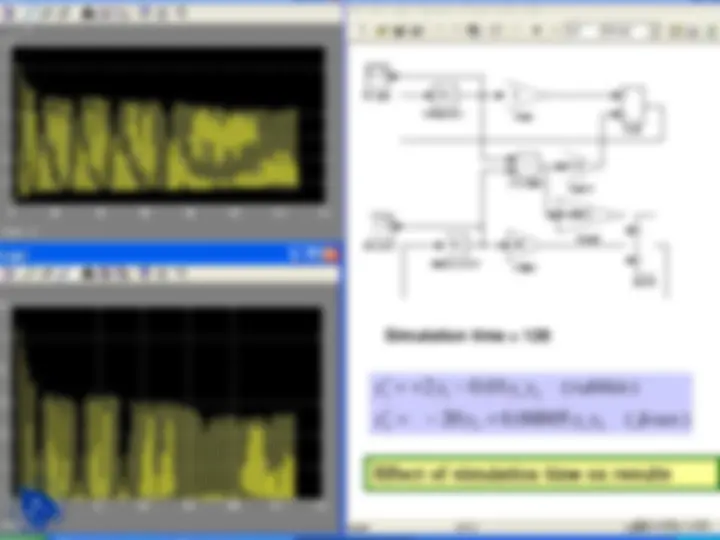
20 0. 0005 ( )
2 0. 01 ( )
2 2 1 2
1 1 1 2
y y y y foxes
y y y y rabbits
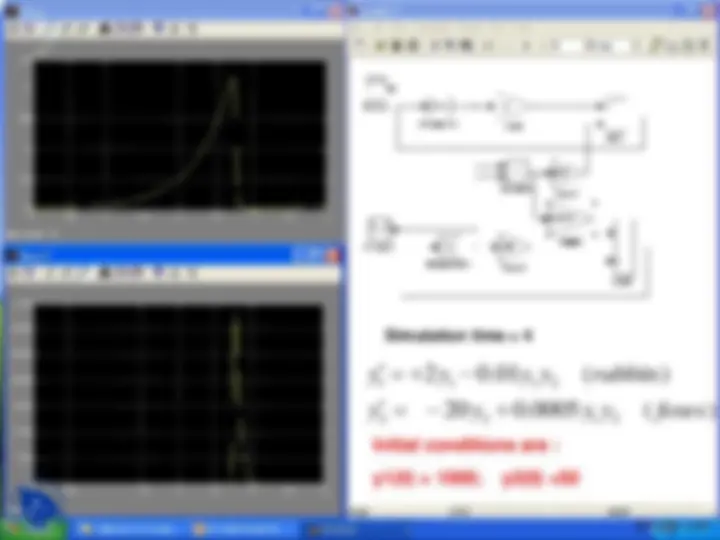
Initial conditions are :
y1(0) = 1000; y2(0) =
Simulation time = 4
2 2 1 2
1 1 1 2
y y y y foxes
y y y y rabbits
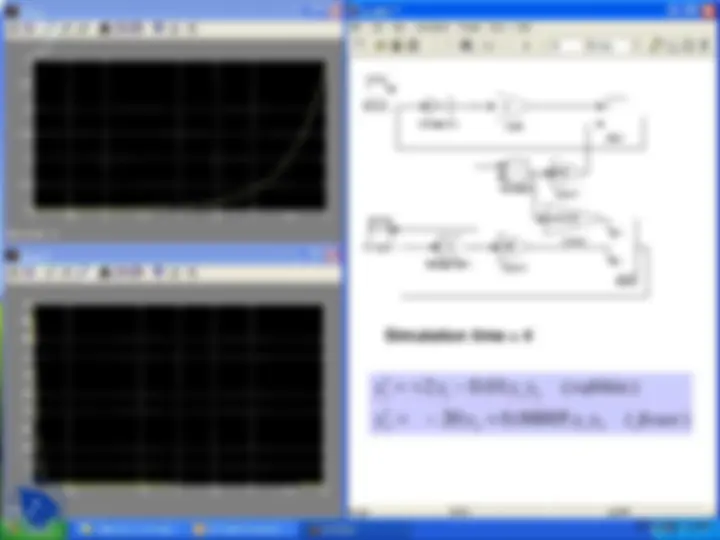
Effect of simulation time on results
Simulation time = 8
2 2 1 2
1 1 1 2
y y y y foxes
y y y y rabbits
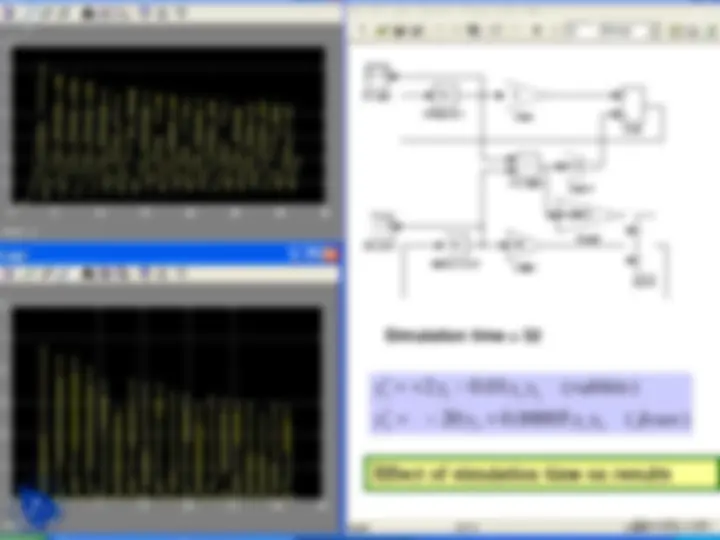
Effect of simulation time on results
Simulation time = 16
2 2 1 2
1 1 1 2
y y y y foxes
y y y y rabbits
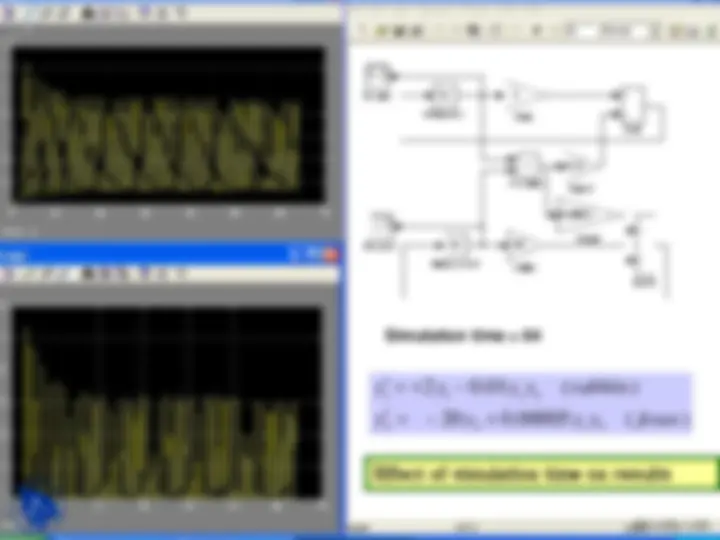
Effect of simulation time on results
Simulation time = 64
2 2 1 2
1 1 1 2
y y y y foxes
y y y y rabbits
Effect of simulation time on results
Simulation time = 128