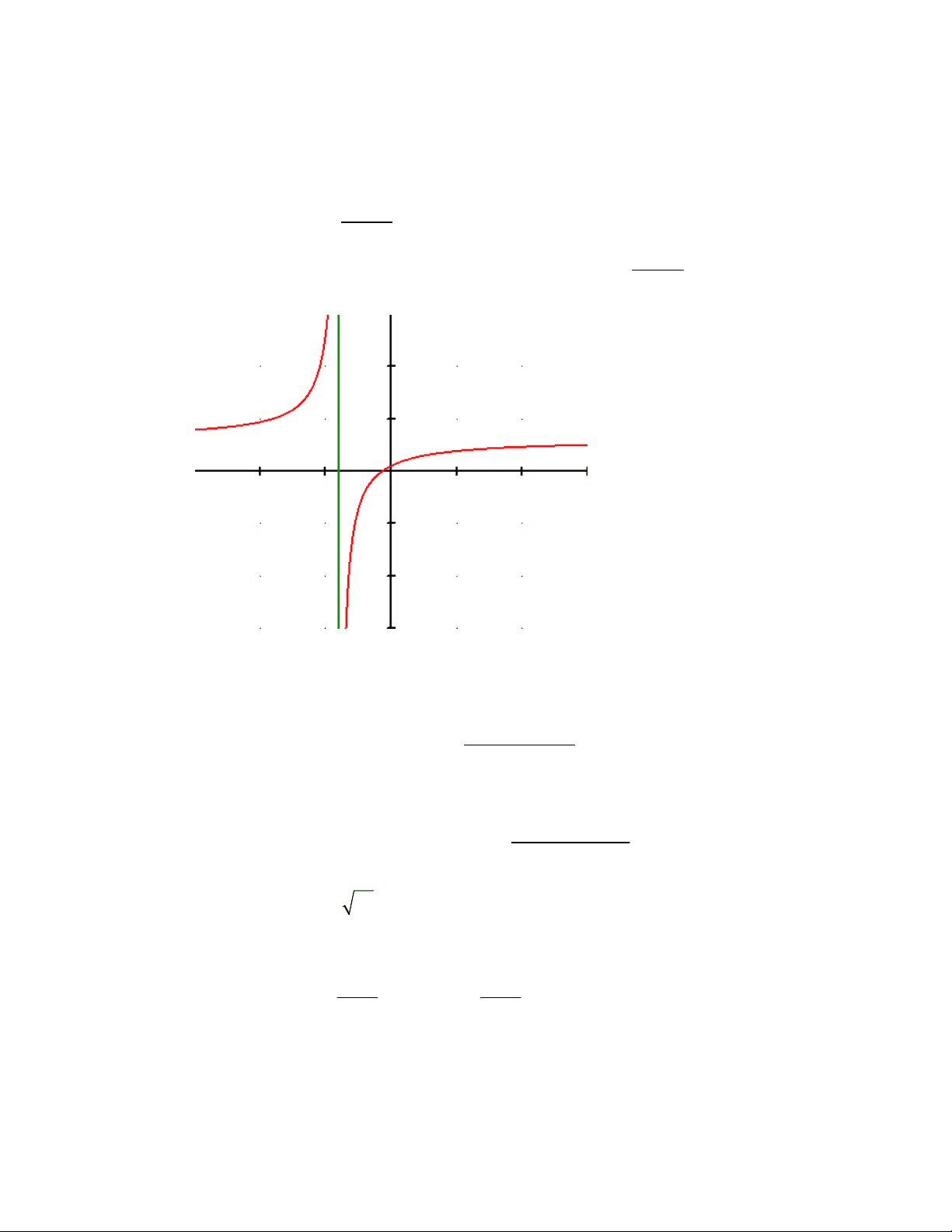




Study with the several resources on Docsity

Earn points by helping other students or get them with a premium plan


Prepare for your exams
Study with the several resources on Docsity

Earn points to download
Earn points by helping other students or get them with a premium plan
Community
Ask the community for help and clear up your study doubts
Discover the best universities in your country according to Docsity users
Free resources
Download our free guides on studying techniques, anxiety management strategies, and thesis advice from Docsity tutors
Practice problems for exam 2 of math 12, focusing on solving inequalities using graphs, sketching quadratic functions and labeling their vertices, intercepts, and x-intercepts, simplifying difference quotients, finding the domain of a function, and evaluating functions. Additionally, it covers finding the domain of a composite function, evaluating functions at given values, finding the domain of a rational function, and using synthetic division and the remainder theorem.
Typology: Exams
1 / 4

This page cannot be seen from the preview
Don't miss anything!
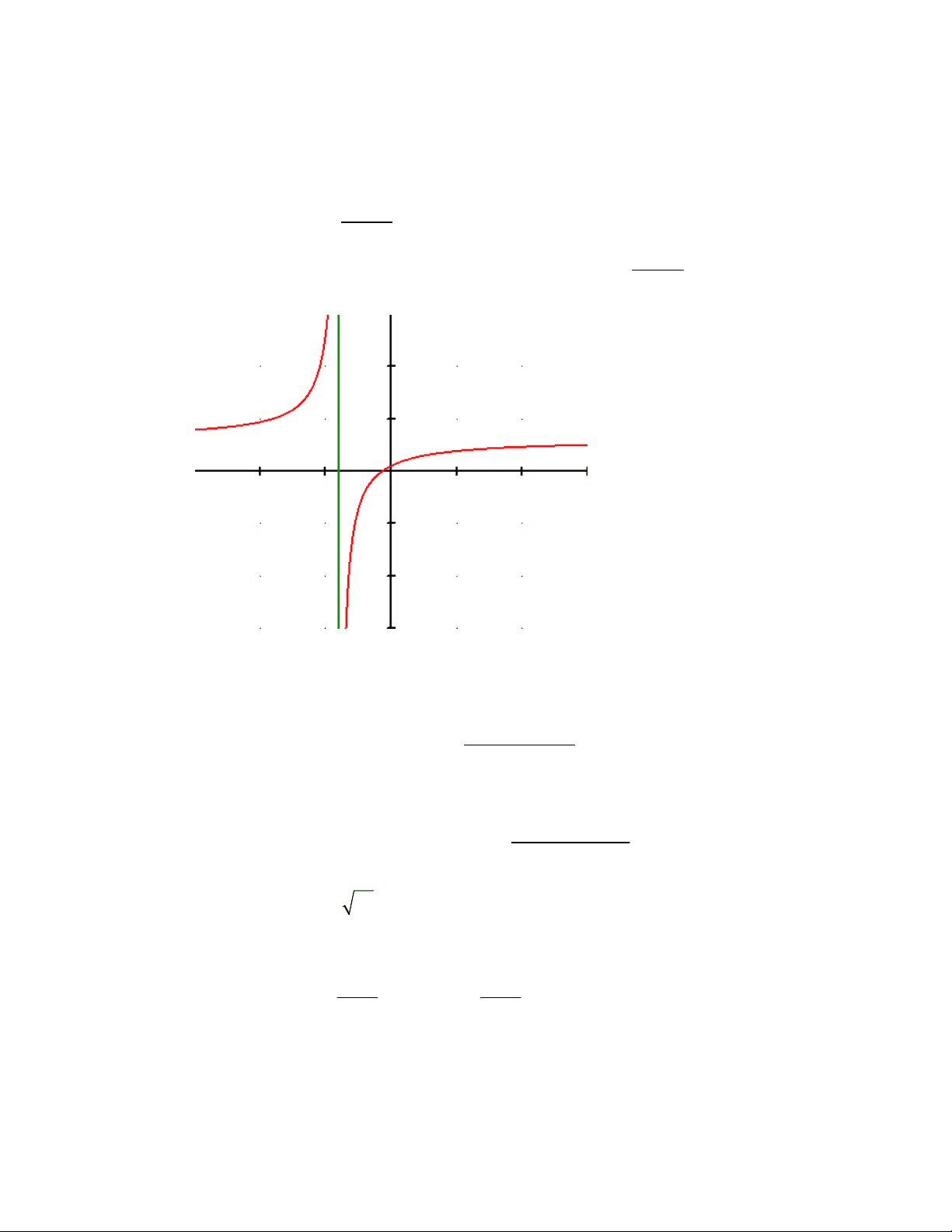


x y x
and the graph of the vertical line x = − 4 are
shown below. Use this graph to solve the inequality
x
x
2 y = − x + 6 x − 5. Label the
vertex, the y-intercept, and the x-intercepts.
f x ( h ) f x (
h
, for the function
2 f x ( ) = x + 5 x
x f x x x 8
b. Let
f x x
and
g x x
3 2 f x ( ) = 2 x − 4 x + 3 x
a. f (2 )
b. f ( −1)
c. f (2 x )
f x x
5 3 ( ) 2 3 4
x P x = − x + x −
4 2 Q x ( ) = 12 x − 5 x + 1
3 2 R x ( ) = x + x + 1
Which function is symmetric with respect to the y-axis?
Which function is symmetric with respect to the origin?
Explain your answer.
Graph the function y = − x − 2 + 3 on the same set of axes.
−8 −7 −6 −5 −4 −3 −2 −1 1 2 3 4 5 6 7 8 9
−
−
−
−
−
−
−
−
1
2
3
4
5
6
7
8
4 3 3 2 4
x x x
x
Express the answer in the form P(x) = (x – a)Q(x) + R.
For each graph, each tick mark represents one unit.
−8 −7 −6 −5 −4 −3 −2 −1 1 2 3 4 5 6 7 8 9
−
−
−
−
−
−
−
−
1
2
3
4
5
6
7
8
−8 −7 −6 −5 −4 −3 −2 −1 1 2 3 4 5 6 7 8 9
−
−
−
−
−
−
−
−
1
2
3
4
5
6
7
8
−8 −7 −6 −5 −4 −3 −2 −1 1 2 3 4 5 6 7 8 9
−
−
−
−
−
−
−
−
1
2
3
4
5
6
7
8
−8 −7 −6 −5 −4 −3 −2 −1 1 2 3 4 5 6 7 8 9
−
−
−
−
−
−
−
−
1
2
3
4
5
6
7
8
−8 −7 −6 −5 −4 −3 −2 −1 1 2 3 4 5 6 7 8 9
−
−
−
−
−
−
−
−
1
2
3
4
5
6
7
8
−8 −7 −6 −5 −4 −3 −2 −1 1 2 3 4 5 6 7 8 9
−
−
−
−
−
−
−
−
1
2
3
4
5
6
7
8