Equivalence - Automata and Complexity Theory - Lecture Slides, Slides of Theory of Automata

Download Equivalence - Automata and Complexity Theory - Lecture Slides and more Slides Theory of Automata in PDF only on Docsity!

1

Equivalence of PDA, CFG

Conversion of CFG to PDAConversion of PDA to CFG

2

Overview

When we talked about closure properties of regular languages, it wasuseful to be able to jump between REand DFA representations.

Similarly, CFG’s and PDA’s are both useful to deal with properties of theCFL’s.

4

Converting a CFG to a PDA

Let L = L(G).

Construct PDA P such that N(P) = L.

P has:



One state q.



Input symbols = terminals of G.



Stack symbols = all symbols of G.



Start symbol = start symbol of G.

5

Intuition About P

Given input w, P will step through a leftmost derivation of w from the startsymbol S.

Since P can’t know what this derivation is, or even what the end of w is, it usesnondeterminism to “guess” theproduction to use at each step.

7

Transition Function of P

δ

(q, a, a) = (q,

ε

Type 1

rules)



This step does not change the LSFrepresented, but “moves” responsibility for

a

from the stack to the consumed input.

If A ->

is a production of G, then

δ

(q,

ε

, A) contains (q,

Type 2

rules)



Guess a production for A, and represent thenext LSF in the derivation.

8

Proof That L(P) = L(G)

We need to show that (q, wx, S)

(q, x,

) for any x if and only if

S =>*

lm

w

Part 1: “only if” is an induction on the number of steps made by P.

Basis: 0 steps.



Then



= S, w =

ε

, and S =>*

lm

S is

surely true.

10

Use of a Type 1 Rule

The move sequence must be of the form (q, yax, S)

• (q, ax, a

(q, x,

where ya = w.

By the IH applied to the first n-1 steps, S =>*

lm

ya

But ya = w, so S =>*

lm

w

11

Use of a Type 2 Rule

The move sequence must be of the form (q, wx, S)

• (q, x, A

(q, x,

where A ->

is a production and

By the IH applied to the first n-1 steps, S =>*

lm

wA

Thus, S =>*

lm

w

= w

13

Proof – Completion

We now have (q, wx, S)

• (q, x,

) for

any x if and only if

S =>*

lm

w

In particular, let x =

ε

Then (q, w, S)

• (q,

ε

ε

) if and only if

S =>*

lm

w.

That is, w is in N(P) if and only if w is in L(G).

14

From a PDA to a CFG

Now, assume L = N(P).

We’ll construct a CFG G such that L = L(G).

Intuition: G will have variables generating exactly the inputs that cause P to have thenet effect of popping a stack symbol Xwhile going from state p to state q.



P never gets below this X while doing so.

16

Productions of G

Each production for [pXq] comes from a move of P in state p with stack symbol X.

Simplest case:

δ

(p, a, X) contains (q,

ε

Then the production is [pXq] -> a.



Note

a

can be an input symbol or

ε

.

Here, [pXq] generates

a, because reading

a

is one way to pop X and go from p to q.

17

Productions of G – (2)

Next simplest case:

δ

(p, a, X) contains

(r, Y) for some state r and symbol Y.

G has production [pXq] -> a[rYq].



We can erase X and go from p to q byreading

a

(entering state r and replacing

the X by Y) and then reading some w thatgets P from r to q while erasing the Y.

Note: [pXq] =>* aw whenever [rYq] =>* w.

19

Picture of Action of P

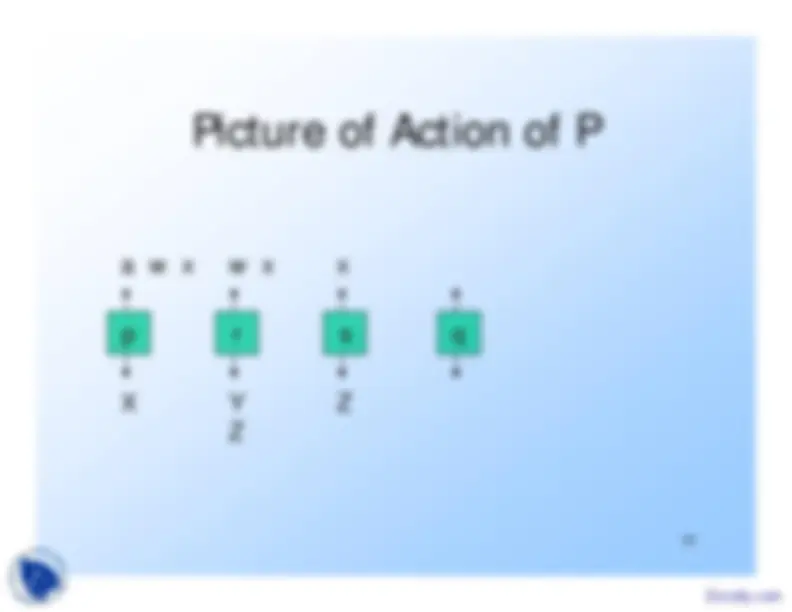
a p X

w

x

r w Y Z

x

s x Z

q

20

Third-Simplest Case – Concluded

Since we do not know state s, we must generate a family of productions:

[pXq] -> a[rYs][sZq]

for all states s.

[pXq] =>* awx whenever [rYs] =>* w and [sZq] =>* x.