


Study with the several resources on Docsity

Earn points by helping other students or get them with a premium plan


Prepare for your exams
Study with the several resources on Docsity

Earn points to download
Earn points by helping other students or get them with a premium plan
Community
Ask the community for help and clear up your study doubts
Discover the best universities in your country according to Docsity users
Free resources
Download our free guides on studying techniques, anxiety management strategies, and thesis advice from Docsity tutors
Main points of this past exam are: Enjoy, Venn Diagram, Helping People, Sue, Invalid, Argument, Symbolic Statement
Typology: Exercises
1 / 3

This page cannot be seen from the preview
Don't miss anything!


score
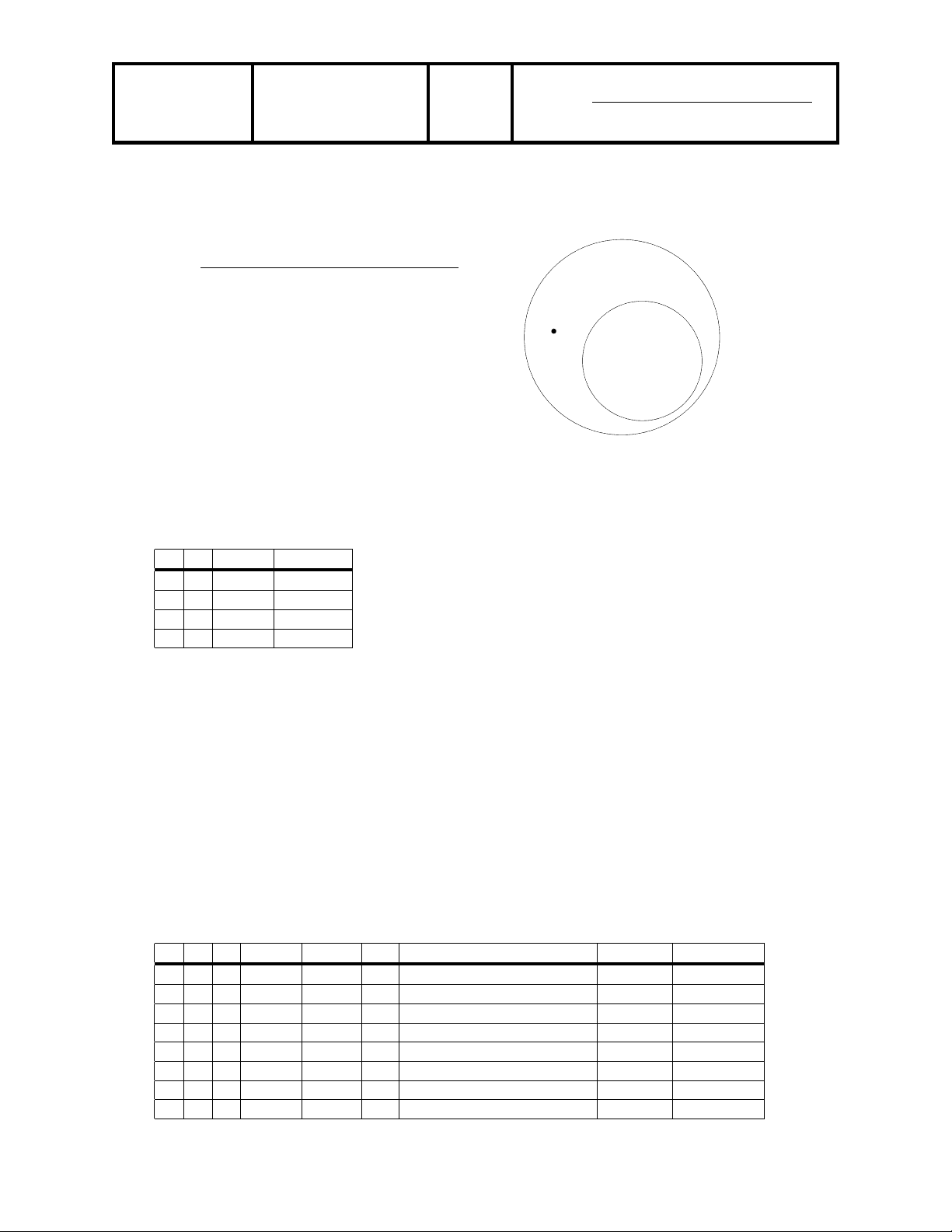
Solution: The argument is invalid. From the Venn dia- gram, we see Sue can enjoy helping while not being a politician.
Politicians
those who enjoy helping people
Sue
Solution: p q p → q (^) ˜ q → (^) ˜ p T T T T T F F F F T T T F F T T
The last two columns agree, so the statement p → q is logically equivalent to ˜ q → (^) ˜ p.
Solution: Use the symbolic representations p : a student studies regularly; q : the student does well in school; r : the student’s teachers are good. Then the paragraph can be written as ( (p → q) ∧ (r → q) ∧ ( ˜ q)
˜ p^ ∨^ ˜ r
which turns out to be a tautology, so the argument is valid. p q r p → q r → q (^) ˜ q (p → q) ∧ (r → q) ∧ ( ˜ q) (^) ˜ p ∨ (^) ˜ r paragraph T T T T T F F F T T T F T T T T T T T F T F F F F F T T F F F T T F T T F T T T T F T T T F T F T T T T T T F F T T F F F T T F F F T T T T T T
Solution: Statement (c) is the contrapositive of statement (b), so they are logically equivalent. Statement (b) is the converse of (a) so they aren’t equivalent.
Solution: Beginning with the universal set U , just delete all elements that are in A ∩ B to get (A ∩ B) ′^ = { b, d, e, f , g, h, i, l }. The Venn diagram for (A ∪ B) ′^ is shown to the right.
A B
U
Solution: We know that n(A ∪ B) = n(A) + n(B) − n(A ∩ B). Since we are given that 61 like neither, we know that 250 − 61 = 189 like at least one, so n(A ∪ B) = 189. So 189 = 164 + 128 − n(A ∩ B). Thus, n(A ∩ B) = 102.
63 102
61
Ba
ske tball Baseb all
24
Solution: Using the formulas we have 7 P 3 = (^) ( 7 −7! 3 )! = 7 · 6 · 5 = 210 and 7 C 3 = (^) ( 7 −7! 3 ) !3! = 73 ·^6 · 2 ·^5 = 35. For counting problems, you could say:
From a group of 7 people, we want to select 3 and line them up in a row (answer 7 P 3 ). From a group of 7 people, we want to select 3 to form a committee (answer 7 C 3 ).