







Study with the several resources on Docsity

Earn points by helping other students or get them with a premium plan


Prepare for your exams
Study with the several resources on Docsity

Earn points to download
Earn points by helping other students or get them with a premium plan
Community
Ask the community for help and clear up your study doubts
Discover the best universities in your country according to Docsity users
Free resources
Download our free guides on studying techniques, anxiety management strategies, and thesis advice from Docsity tutors
An introduction to digital logic, focusing on switches, functions, and gates. It covers binary values, transistors as switches, logical and and or functions, and the seven common logic primitives. The document also explains how logic gates can be implemented using various technologies and universal logic families. Lastly, it discusses the digital design process and converting boolean algebra into gates.
Typology: Slides
1 / 13

This page cannot be seen from the preview
Don't miss anything!








Apps
O/S
Arch
mArch
Logic
Digital
Analog
Devices
Physics
x = 0 x = 1
S
x
S
x Power supply S
x
S
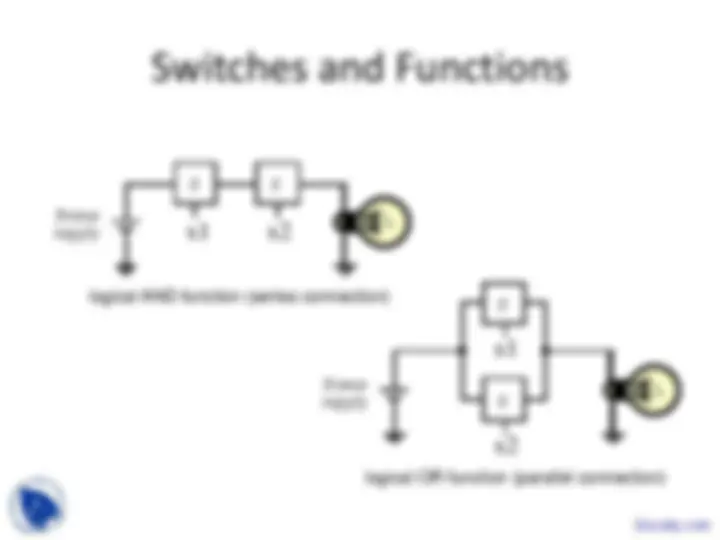
x3 L
Seven Common Logic Primitives
Universal Logic Families:
Apps
O/S
Arch
mArch
Logic
Digital
Analog
Devices
Physics
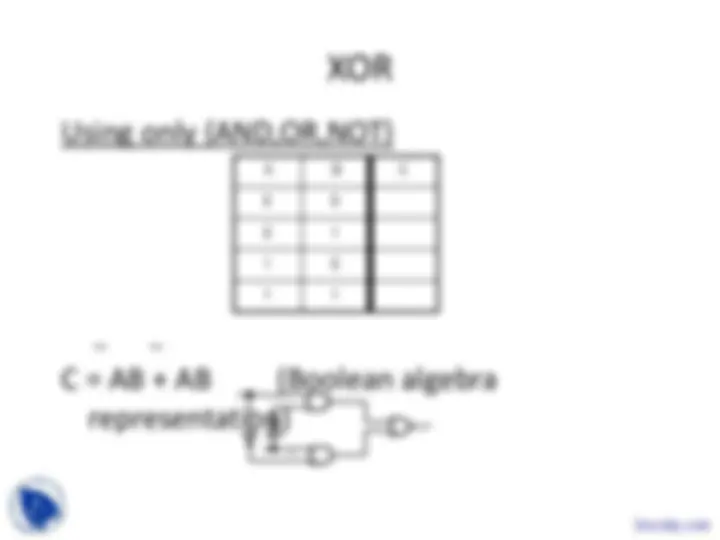
A
B
C
S
A
B
C
S
S
B
A C
0 1 S
B
A C
0 1 S
B
A C
0 1