Short Version : 22. Electric Potential
Docsity.com
Prepare for your exams
Study with the several resources on Docsity
Earn points to download
Earn points by helping other students or get them with a premium plan
Guidelines and tips
Prepare for your exams
Study with the several resources on Docsity
Earn points to download
Earn points by helping other students or get them with a premium plan
Community
Ask the community
Ask the community for help and clear up your study doubts
University Rankings
Discover the best universities in your country according to Docsity users
Free resources
Our save-the-student-ebooks!
Download our free guides on studying techniques, anxiety management strategies, and thesis advice from Docsity tutors
Electricity Potential - General Physcis - Lecture Slides, Slides of Physics
Physics is about nature. This course covers almost every concept related to physics. Important points in this lecture are: Electric Potential, Electric Potential Difference, Force, Field, Potential Energy, Path Independent, Charged Sheet, Calculating Potential Difference, the Zero of Potential, Science Museum
Typology: Slides
2012/2013
1 / 24
This page cannot be seen from the preview
Don't miss anything!
Related documents
Partial preview of the text
Download Electricity Potential - General Physcis - Lecture Slides and more Slides Physics in PDF only on Docsity!
Short Version :
22. Electric Potential
22.1. Electric Potential Difference
Conservative force:
AB
B^
A
U
U
U
AB W
B A^
d
F
r
Electric potential difference
electric potential energy difference per unit charge B A^
d
E
r
AB
AB
U
V
q
B V
if reference potential V
A
= 0.
[ V ] = J/C = Volt = V
For a uniform field:
AB
AB
V
E r
^
B^
A
^
E
r
r
( path independent )
r
AB
E Docsity.com
Potential Difference is Path Independent
Potential difference
V
AB
depends only on positions of
A
&
B
.
Calculating along any paths (1, 2, or 3) gives
V
AB
=
E
r.
Example 22.2.
Charged Sheet
An isolated, infinite charged sheet carries a uniform surface charge density
.
Find an expression for the potential difference from the sheet to a point aperpendicular distance
x
from the sheet.
^
0
x V
E
x
0 2
x
^
E
The Zero of Potential
Only potential differences have physical significance.
Simplified notation:
RA
A^
R^
A
V
V
V
V
R = point of zero potential
V
A
= potential at
A
.
Some choices of zero potential
Power systems / Circuits
Earth ( Ground )
Automobile electric systems
Car’s body
Isolated charges
Infinity
Example 22.3.
Science Museum
The Hall of Electricity at the Boston Museum of Science contains a large Van de Graaff generator, a devicethat builds up charge on a metal sphere.The sphere has radius
R
= 2.30 m and develops a charge
Q
= 640
C.
Considering this to be a single isolate sphere, find(a) the potential at its surface,(b) the work needed to bring a proton from infinity to the sphere’s surface,(c) the potential difference between the sphere’s surface & a point 2
R
from its center.
^
^
Q
V
R
k
R
^
^
6
9
/^
C
Vm
C
m
(a)
M
V
^
W
e V
R
(b)
M
eV
^
19
C
MV
13
J
^
^
^
,
R^
R
V
V
R
V
R
(c)
Q 2
Q
k
k
R
R
Q 2
k
R
M
V
Finding Potential Differences Using Superposition
Potential of a set of point charges:
^
^
i
i^
P^
i
q
V
P
k
r
r
Potential of a set of charge sources:
^
^
^
i
i
V
P
V
P
Example 22.5.
Dipole Potential
An electric dipole consists of point charges
q
a distance 2
a
apart.
Find the potential at an arbitrary point
P
, and approximate for the casewhere
the distance to
P
is large compared with the charge separation.
^
^
^
1
q 2
q
V
P
k
k
r
r
1
2
kq
r^
r
^
^
^
2
2
2
1
cos
r^
r^
a
r a
2
2
2
2
cos
r^
r^
a
r a
2
2
2
1
cos
r
r^
r a
^
2
1
1
2
r^
r
r^
r
r^
a
2
1
cos
r^
r^
a
^
^
2
1 2 r
r
V
P
k q
r
2
cos
qa
k
r
2 cos p k
r
p
= 2
qa
= dipole moment
2
1
2
1
r^
r
kq
r r
+q: hill
q: hole
V = 0
Docsity.com
Example 22.6.
Charged Ring
A total charge
Q
is distributed uniformly around a thin ring of radius
a
.
Find the potential on the ring’s axis.
^
^
dq
V
x
k
r
2
2
k
dq
x
a
2
2
k
Q
x
a
Same
r
for all
dq
Q
k
x
a
x
Example 22.7.
Charged Disk
A charged disk of radius
a
carries a charge
Q
distributed uniformly over its surface.
Find the potential at a point
P
on the disk axis, a distance
x
from the disk.
^
V
x
dV
2
2
k
dq
x
r
^
2
2
2 2
k Q
x
a
x
a
2
2
0
a^
k
Q
r dr
a
x
r
2
2
2
0
a
Q
r
k
dr
a
x
r
2
2
2
0
a
Q
k
x
r
a
sheet
point charge
disk
^
2
0
k Q
kQ
a
x
x
x
a
a
a
k Q
x
a
x
Calculating Field from Potential
r^ B A
AB
r
V
d
E
r
dV
d
E
r
i^
i
i
E dx
i
i^
i V
d x x
i
i V
E
x
V
E
=
( Gradient of V )
V
V
V
x
y
z
E
i^
j^
k
E
is strong where V changes rapidly ( equipotentials dense ).
Example 22.8.
Charged Disk
Use the result of Example 22.7 to find
E
on the axis of a charged disk.
Example 22.7:
^
^
^
2
2
2 2
k Q
V
x
x
a
x
a
2
2
2
k Q
x
a
x
a
x
V
E
x
x > 0x < 0
y^
z
E
E
dangerous conclusion
22.4. Charged Conductors
In electrostatic equilibrium,
E
= 0
inside a conductor.
E
//^
= 0
on surface of conductor.
W = 0 for moving charges on / inside conductor.
The entire conductor is an equipotential.
Consider an isolated, spherical conductor of radius
R
and charge
Q
.
Q
is uniformly distributed on the surface
E
outside is that of a point charge
Q
.
V
( r
) =
k Q
/
R
.^
for
r
R
.
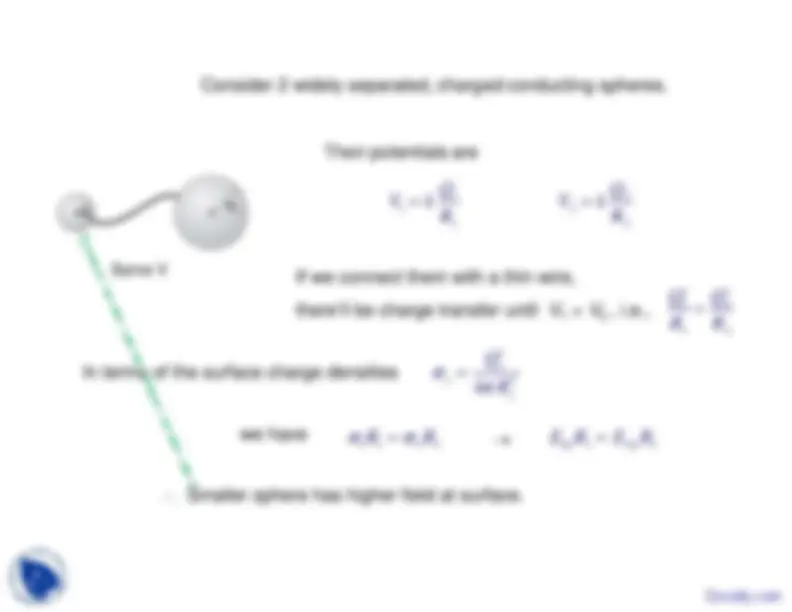
Consider 2 widely separated, charged conducting spheres.
1
1
1 Q
V
k
R
2
2
2 Q
V
k
R
Their potentials are
If we connect them with a thin wire,there’ll be charge transfer until
V
1
=
V
2
, i.e.,
1
2
1
2
Q
Q
R
R
^
2
j
j
j
Q
R
In terms of the surface charge densities
1
1
2
2
R
R
we have
Smaller sphere has higher field at surface.
1
1
2
2
E
R
E
R
Same V
Docsity.com