Download Dislocations and Strengthening - Science and Engineering of Materials - Lecture Slides and more Slides Materials science in PDF only on Docsity!
Dislocations and Strengthening
What is happening during plastic deformation?
Chapter Outline
Dislocations and Plastic Deformation Motion of dislocations in response to stress Slip Systems Plastic deformation in single crystals polycrystalline materials
Strengthening mechanisms Grain Size Reduction Solid Solution Strengthening Strain Hardening
Recovery, Recrystallization, and Grain Growth
Not tested: 7.7 Deformation by twinning, Direction and plane nomenclature in §7.4.
How do metals plastically deform?
Why does forging change properties?
Why deformation occurs at stresses smaller than those for perfect crystals?
Introduction
Taylor, Orowan and Polyani 1934 :
Plastic deformation due to motion of
large number of dislocations.
Plastic deformation under shear stress
Direction of Dislocation Motion
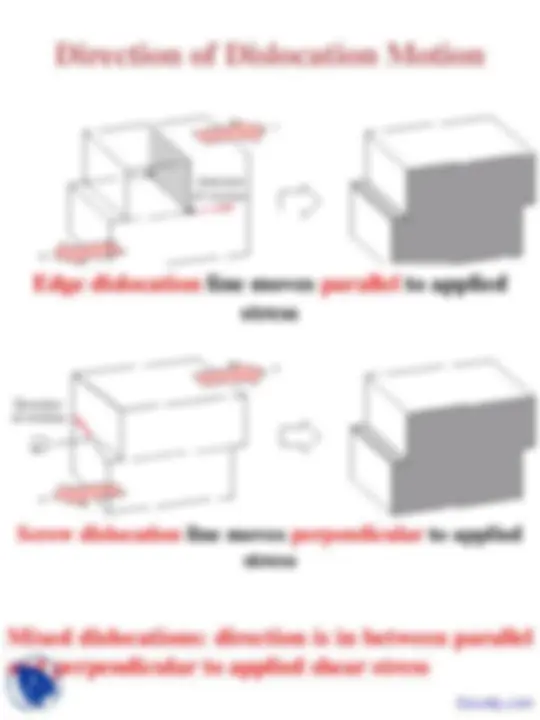
Mixed dislocations: direction is in between parallel and perpendicular to applied shear stress
Edge dislocation line moves parallel to applied stress
Screw dislocation line moves perpendicular to applied stress
Strain Field around Dislocations
Edge dislocations compressive, tensile, and shear lattice strains.
Screw dislocations shear strain only.
Strain fields from distortions at dislocations: Drops radially with distance.
Dislocation density dislocation length/ volume OR number of dislocations intersecting a unit area. 10 5 cm -2^ in carefully solidified metal crystals to 10^12 cm-2^ in heavily deformed metals.
Where do Dislocations Come From?
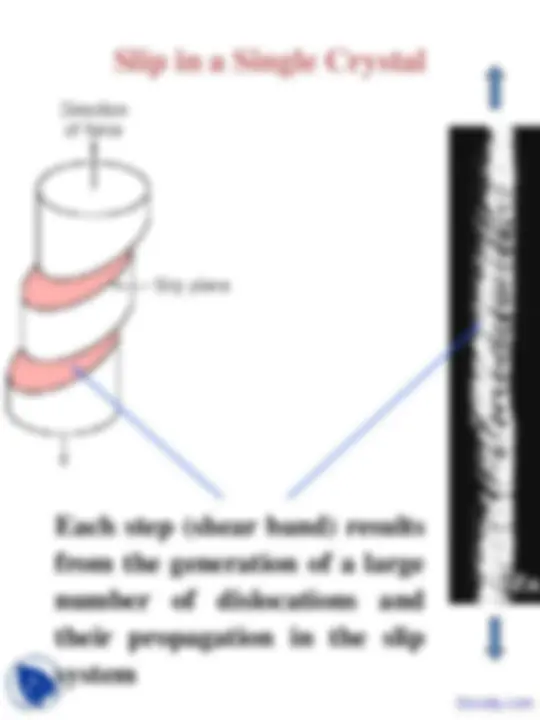
Most crystalline materials have dislocations due to stresses associated with the forming process. Number increases during plastic deformation. Spawn from dislocations, grain boundaries, surfaces. Picture is snapshot from simulation of plastic deformation in a fcc single crystal (Cu). See animation at http://zig.onera.fr/lem/DisGallery/3D.html
Slip System
Preferred planes for dislocation movement (slip planes) Preferred crystallographic directions (slip directions) Slip planes + directions (slip systems) highest packing density.
Distance between atoms shorter than average; distance perpendicular to plane longer than average. Far apart planes can slip more easily. BCC and FCC have more slip systems compared to HCP: more ways for dislocation to propagate ⇒ FCC and BCC are more ductile than HCP.
Resolving (Projecting) Applied Stress onto Slip System
Dislocations move along particular planes and directions (the slip system) in response to shear stresses along these planes and directions ⇒ Applied stress is resolved onto slip systems?
τ (^) R = σcosφcos λ
Resolved shear stress, τR,
Deformation due to tensile stress, σ.
φ
λ
Slip in Single Crystals Critical Resolved Shear Stress
Resolved shear stress increases crystal will start to yield (dislocations start to move along most favorably oriented slip system).
Onset of yielding yield stress, σy. Minimum shear stress to initiate slip:
Critical resolved shear stress:
τCRSS = σy (cos φcosλ)MAX
Maximum of (cosφ cosλ) φ = λ = 45 o^ ⇒ cosφ cosλ = 0.5 ⇒ σy = 2τCRSS
( )MAX
CRSS y
cos φcosλ
Slip occurs first in slip systems oriented close to (φ = λ = 45 o^ ) with respect to the applied stress
Plastic Deformation of Polycrystalline Materials
Larger plastic deformation corresponds to
elongation of grains along direction of
applied stress.
Before After
Plastic Deformation of Polycrystalline Materials
Polycrystalline metals are typically stronger than single crystals. WHY?
Slip directions vary from crystal to crystal ⇒ Some grains are unfavorably oriented with respect to the applied stress (i.e. cosφ cosλ low)
Even those grains for which cosφ cosλ is high may be limited in deformation by adjacent grains which cannot deform so easily
Dislocations cannot easily cross grain boundaries because of changes in direction of slip plane and disorder at grain boundary
Strengthening by grain-size reduction (I)
Small angle grain boundaries are not very effective.
High-angle grain boundaries block slip and increase strength of the material.
Grain boundaries are barriers to dislocation motion: slip plane discontinues or change orientation.
Strengthening by grain-size reduction (II)
Finer grains larger area of grain boundaries to impede dislocation motion: also improves toughness. Hall-Petch equation:
σo and k (^) y constants for particular material d is the average grain diameter.
d determined by rate of solidification, by plastic deformation and by heat treatment.
σy = σ 0 +k y d
70 Cu - 30 Zn brass alloy
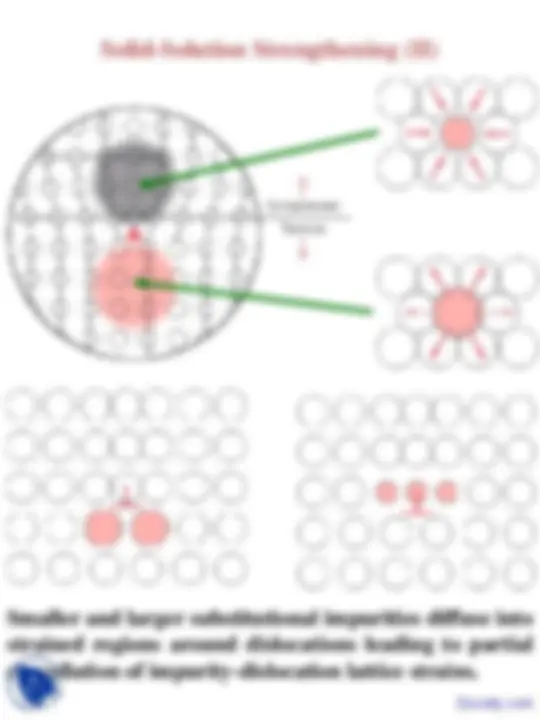
Solid-Solution Strengthening (II)
Smaller and larger substitutional impurities diffuse into strained regions around dislocations leading to partial cancellation of impurity-dislocation lattice strains.
