Direct Method of Interpolation - Numerical Methods - Lecture Slides, Slides of Mathematical Methods for Numerical Analysis and Optimization

Download Direct Method of Interpolation - Numerical Methods - Lecture Slides and more Slides Mathematical Methods for Numerical Analysis and Optimization in PDF only on Docsity!

Direct Method of Interpolation

What is Interpolation?

Given (x 0 ,y 0 ), (x 1 ,y 1 ), …… (xn,yn), find the value of ‘y’ at a

value of ‘x’ that is not given.

Figure 1 Interpolation of discrete.

Direct Method

0 1

n n

y  a  a x   a x

Given ‘n+1’ data points (x 0 ,y 0 ), (x 1 ,y 1 ),………….. (xn,yn),

pass a polynomial of order ‘n’ through the data as given

below:

where a 0 , a 1 ,………………. an are real constants.

• Set up ‘n+1’ equations to find ‘n+1’ constants.
• To find the value ‘y’ at a given value of ‘x’, simply substitute

the value of ‘x’ in the above polynomial.

Example 1

The upward velocity of a rocket is given as a function of time in Table 1.

Find the velocity at t=16 seconds using the direct method for linear interpolation.

0 0

10 227.

15 362.

20 517.

22.5 602.

30 901.

Table 1 Velocity as a function

of time.

Figure 2 Velocity vs. time data for the rocket example

t , s v    t , m/s 

Example 2

The upward velocity of a rocket is given as a function of time in Table 2.

Find the velocity at t=16 seconds using the direct method for quadratic interpolation.

0 0

10 227.

15 362.

20 517.

22.5 602.

30 901.

Table 2 Velocity as a function

of time.

Figure 5 Velocity vs. time data for the rocket example

t , s v    t , m/s 

Quadratic Interpolation

2 v t  a 0  a 1 t  a 2 t

2 v  a 0  a 1  a 2 

2 v  a 0  a 1  a 2 

2 v  a 0  a 1  a 2 

Solving the above three equations gives

0

a  17. 733

1

a  0. 3766

2

a 

Quadratic Interpolation

 (^) x 0 , y 0 

 x 1 , y 1   x 2 , y 2 

f 2   x

y

x Figure 6 Quadratic interpolation.

Example 3

The upward velocity of a rocket is given as a function of time in Table 3.

Find the velocity at t=16 seconds using the direct method for cubic interpolation.

0 0

10 227.

15 362.

20 517.

22.5 602.

30 901.

Table 3 Velocity as a function

of time.

Figure 6 Velocity vs. time data for the rocket example

t , s v    t , m/s 

Cubic Interpolation

v   t^  a 0  a 1 t  a 2 t^2  a 3 t^3

3 3

2 v 10  227. 04  a 0  a 110  a 210  a 10

3 3

2 v 15  362. 78  a 0  a 115  a 2 15  a 15

3 3

2 v 20  517. 35  a 0  a 1 20  a 2 20  a 20

3 3

2 v 22. 5  602. 97  a 0  a 1 22. 5  a 2 22. 5  a 22. 5

a 0  4. 2540 a 1  21. 266 a 2 ^0.^13204 a 3 ^0.^0054347

y

x

f 3   x

 x 3 , y 3 

 (^) x 2 , y 2 

 (^) x 1 , y 1 

 x 0 , y 0 

Figure 7 Cubic interpolation.

Comparison Table

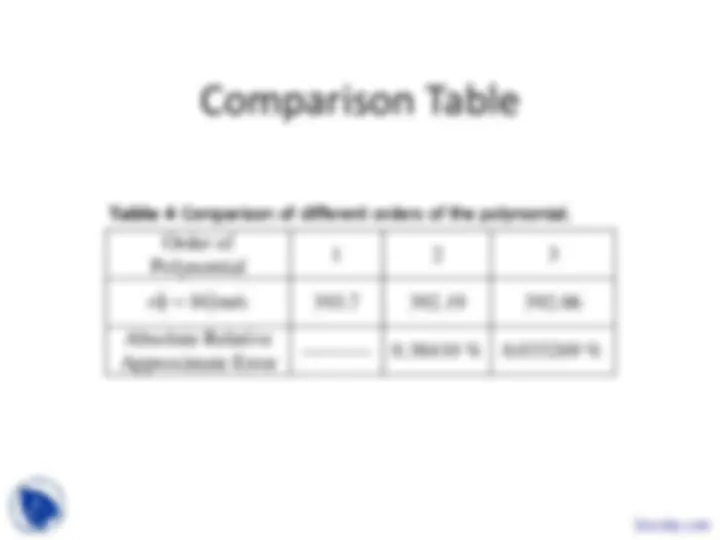
Order of Polynomial

1 2 3

v  t  16  m/s 393.7 392.19 392.

Absolute Relative Approximate Error

---------- 0.38 410 % 0.033269 %

Table 4 Comparison of different orders of the polynomial.

Distance from Velocity Profile

Find the distance covered by the rocket from t=11s to t=16s?

2 3 v t    t  t  t  t 

     

1605 m

4

1. 0054347 3

2. 13204 2

3. 2540 21. 266

4. 2540 21. 266 0. 13204 0. 0054347

16 11

16

11

2 3 4

16

11

2 3

16

11



 

  

     

    

 

t t t t

t t t dt

s s v t dt