digital logic design and binary systems, Lecture notes of Digital Logic Design and Programming

Download digital logic design and binary systems and more Lecture notes Digital Logic Design and Programming in PDF only on Docsity!

Introduction to digital systems

Juan P Bello

Analogue vs Digital (1) •^ Analog information is made up of a continuum of values within a^ given range •^ At its most basic, digital information can assume only one of two^ possible values: one/zero, on/off, high/low, true/false, etc.

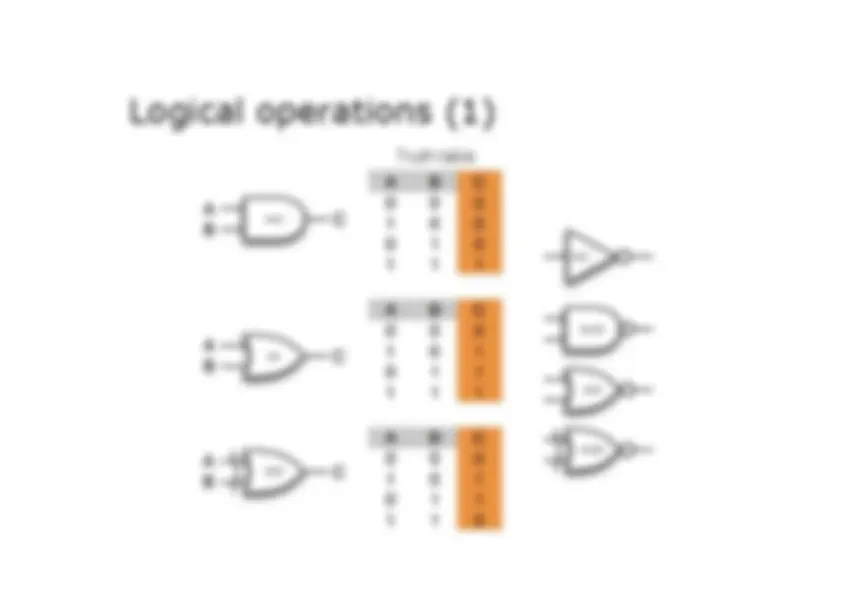
Logical operations (1)

Truth table

Logical operations (2) •^ These logic gates are the basic building blocks of all digital^ systems

Binary system (1) •^ Digital systems represent information using a binary system,^ where data can assume one of only two possible values: zero or^ one. •^ Appropriate for implementation in electronic circuitry, where^ values are characterized by the absence/presence of an electrical^ current flow. •^ Pulse code modulation (PCM) is used to represent binary numbers^ electrically, as a string of high and low voltages

Binary system (2) •^ The binary system represents numbers using

bi nary digi ts^ ( bits

where each digit corresponds to a power of two. • The total (in decimal) is

-^ Since we begin counting from zero,

n^ bits can represent 2

n^ values:

binary^ n from 0 to 2–1 inclusive (e.g. 256 values, from 0 to 255, for 8 bits). • Groups of bits form binary words 1 1 1 0

0 1 0

1

Power of two^^2

7 6 5 4 222

3 2 1 02222 decimal^^128

64 32 16

8 4 2 1

Binary system (4) •^ How to convert from decimal to binary? •^ Repeat division

• by
  • • Example: Convert
  • to binary
    • – 29/2 = 14 remainder 1 (LSB) – 14/2 = 7 remainder 0 – 7/2 = 3 remainder 1 – 3/2 = 1 remainder 1 – 1/2 = 0 remainder 1 (MSB) • 29 =>^1110110
• Octal system • To avoid writing down long binary words, it is often easier to use larger base systems. Two commonly-used systems are octal and hexadecimal. • The octal number system is base eight, i.e. values can be represented using an 8-symbol dictionary: 0-7 • To convert from binary to octal, binary numbers are grouped on 3-bits words such that:
  • = 0, 001 = 1, 010 = 2, 011 = 3, 100 = 4, 101 =
    • 5, 110 = 6, and 111 = 7 • To convert from octal to decimal:
      • 1 0 = 2x8+ 4x8=
        • • From decimal to octal (and from there to binary), Repeat divide by 8: – 20/8 = 2 remainder 4 (LSB) – 2/8 = 0 remainder 2 (MSB) –^20 = 24^10

A/D Conversion (1) •^ The conversion of an analog (continuous) voltage x(t) into a^ discrete sequence of numbers x(n) is performed by an Analog-to-^ digital Converter (ADC) •^ The ADC samples the amplitude of the analog signal at regular^ intervals in time, and encodes (quantizes) those values as binary^ numbers. •^ The regular time intervals are known as the sampling period (T

)s

and are determined by the ADC clock. • This period defines the frequency at which the sampling will be done, such that the sampling frequency (in Hertz) is:^ €

fs^ =^1 / Ts

A/D Conversion (2) •^ The outgoing sequence x(n) is a discrete-time signal with^ quantized amplitude •^ Each element of the sequence is referred to as a sample.

ADC

..., x [ n^ −^1 ],

x [ n ], x [ n^ +1],

A/D Conversion (4) •^ What happens when

fs < 2B

-^ There is another, lower-frequency, signal that share samples with^ the original signal (aliasing). •^ Related to the wagon-wheel effect:^ http://www.michaelbach.de/ot/mot_strob/index.html

LPF Anti-aliasing

A/D Conversion (5) •^ The accuracy of the quantization depends on the number of bits^ used to encode each amplitude value from the analog signal. •^ Example: to quantize the position of a control knob, it is^ necessary to determine the nearest point of the scale •^ This conversion implies an error (max. half a point)

fs^ =^ €

1 / Ts

D/A Conversion •^ Just as we used an ADC to go from x(t) to x(n), we can turn a^ discrete sequence into a continuous voltage level using a digital-to-^ analog converter (DAC). •^ However, the quantized nature of the digital signal produces a “Zero-^ Order Hold” effect that distorts the converted signal, introducing some^ step (fast) changes (know as

imaging).

-^ To avoid this, we use an anti-imaging filter (AKA smoothing or^ reconstruction filter) that smoothes out those fast changes.

Useful References •^ Francis Rumsey (1994). “MIDI Systems and Control”, Focal Press.^ –^ Chapter 1: An Introduction to Computer Systems and Terminology •^ Francis Rumsey and Tim McCormick (2002). “Sound and Recording: An Introduction”, Focal^ Press.^ –^ Chapter 13: MIDI •^ Peter Lau (2001). “Digital System Tutorial on the Web”, University of Sydney:^ http://www.eelab.usyd.edu.au/digital_tutorial/toc.html •^ Curtis Roads (1996). “The Computer Music Tutorial”, The MIT Press