Download Data structures using C and more Lecture notes Data Structures and Algorithms in PDF only on Docsity!
Introduction to Data Structure
Introduction to Data Structure
Computer is an electronic machine which is used for data processing and manipulation. When programmer collects such type of data for processing, he would require to store all of them in computer’s main memory. In order to make computer work we need to know o Representation of data in computer. o Accessing of data. o How to solve problem step by step. For doing this task we use data structure.
What is Data Structure?
Data structure is a representation of the logical relationship existing between individual elements of data. Data Structure is a way of organizing all data items that considers not only the elements stored but also their relationship to each other. We can also define data structure as a mathematical or logical model of a particular organization of data items. The representation of particular data structure in the main memory of a computer is called as storage structure. The storage structure representation in auxiliary memory is called as file structure. It is defined as the way of storing and manipulating data in organized form so that it can be used efficiently. Data Structure mainly specifies the following four things o Organization of Data o Accessing methods o Degree of associativity o Processing alternatives for information Algorithm + Data Structure = Program Data structure study covers the following points o Amount of memory require to store. o Amount of time require to process. o Representation of data in memory. o Operations performed on that data.
Introduction to Data Structure
Classification of Data Structure
Data Structures are normally classified into two broad categories
- Primitive Data Structure
- Non-primitive data Structure
Data types
A particular kind of data item, as defined by the values it can take, the programming language used, or
the operations that can be performed on it.
Primitive Data Structure
Primitive data structures are basic structures and are directly operated upon by machine instructions. Primitive data structures have different representations on different computers. Integers, floats, character and pointers are examples of primitive data structures. These data types are available in most programming languages as built in type. o Integer: It is a data type which allows all values without fraction part. We can use it for whole numbers. o Float: It is a data type which use for storing fractional numbers. o Character: It is a data type which is used for character values.
DATA STRUCTURE
PRIMITIVE
INTEGER FLOATING POINT
CHARACTER POINTER
NON PRIMITIVE
ARRAY LIST
LINEAR LIST
STACK QUEUE
NON LINEAR LIST
GRAPH TREE
FILE
Introduction to Data Structure
Graph: Graph is a collection of nodes (Information) and connecting edges (Logical relation) between nodes. o A tree can be viewed as restricted graph. o Graphs have many types: Un-directed Graph Directed Graph Mixed Graph Multi Graph Simple Graph Null Graph Weighted Graph
Difference between Linear and Non Linear Data Structure
Linear Data Structure Non-Linear Data Structure
Every item is related to its previous and next time. Every item is attached with many other items.
Data is arranged in linear sequence. Data is not arranged in sequence.
Data items can be traversed in a single run. Data cannot be traversed in a single run.
Eg. Array, Stacks, linked list, queue. Eg. tree, graph.
Implementation is easy. Implementation is difficult.
Operation on Data Structures
Design of efficient data structure must take operations to be performed on the data structures into account. The most commonly used operations on data structure are broadly categorized into following types
- Create The create operation results in reserving memory for program elements. This can be done by declaration statement. Creation of data structure may take place either during compile-time or run-time. malloc() function of C language is used for creation.
- Destroy Destroy operation destroys memory space allocated for specified data structure. free() function of C language is used to destroy data structure.
- Selection Selection operation deals with accessing a particular data within a data structure.
Introduction to Data Structure
- Updation It updates or modifies the data in the data structure.
- Searching It finds the presence of desired data item in the list of data items, it may also find the locations of all elements that satisfy certain conditions.
- Sorting Sorting is a process of arranging all data items in a data structure in a particular order, say for example, either in ascending order or in descending order.
- Merging Merging is a process of combining the data items of two different sorted list into a single sorted list.
- Splitting Splitting is a process of partitioning single list to multiple list.
- Traversal Traversal is a process of visiting each and every node of a list in systematic manner.
Time and space analysis of algorithms
Algorithm
An essential aspect to data structures is algorithms.
Data structures are implemented using algorithms.
An algorithm is a procedure that you can write as a C function or program, or any other language.
An algorithm states explicitly how the data will be manipulated.
Algorithm Efficiency
Some algorithms are more efficient than others. We would prefer to choose an efficient algorithm, so it would be nice to have metrics for comparing algorithm efficiency.
The complexity of an algorithm is a function describing the efficiency of the algorithm in terms of the amount of data the algorithm must process.
Usually there are natural units for the domain and range of this function. There are two main complexity measures of the efficiency of an algorithm
Time complexity
Time Complexity is a function describing the amount of time an algorithm takes in terms of the amount of input to the algorithm.
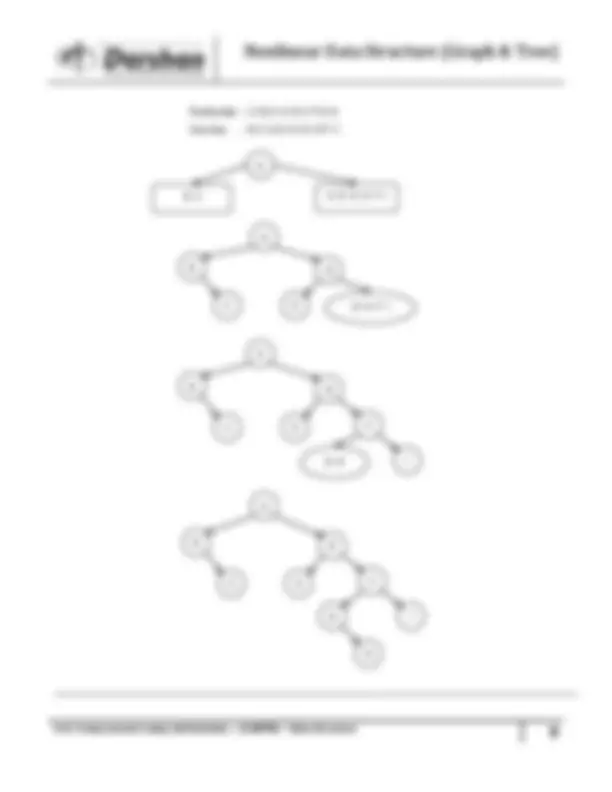
Explain Array in detail
One Dimensional Array Simplest data structure that makes use of computed address to locate its elements is the one- dimensional array or vector; number of memory locations is sequentially allocated to the vector. A vector size is fixed and therefore requires a fixed number of memory locations. Vector A with subscript lower bound of “one” is represented as below….
Two Dimensional Array Two dimensional arrays are also called table or matrix, two dimensional arrays have two subscripts Two dimensional array in which elements are stored column by column is called as column major matrix Two dimensional array in which elements are stored row by row is called as row major matrix First subscript denotes number of rows and second subscript denotes the number of columns Two dimensional array consisting of two rows and four columns as above Fig is stored sequentially by columns : A [ 1, 1 ], A [ 2 , 1 ], A [ 1 , 2 ], A [ 2 , 2 ], A [ 1 , 3 ], A [ 2 , 3 ], A [ 1, 4 ], A [ 2, 4 ] The address of element A [ i , j ] can be obtained by expression Loc (A [ i , j ]) = L 0 + (j-1)2 + i-* In general for two dimensional array consisting of n rows and m columns the address element A [ i , j ] is given by Loc (A [ i , j ]) = L 0 + (j-1)n + (i – 1)* In row major matrix, array can be generalized to arbitrary lower and upper bound in its subscripts, assume that b1 ≤ I ≤ u1 and b2 ≤ j ≤u
For row major matrix : *Loc (A [ i , j ]) = L 0 + ( i – b1 ) (u2-b2+1) + (j-b2)
[ 1 , 1 ] [ 1 , 2 ] [ 1 , 3 ] [ 1 ,m ]
[ 2 , 1 ] [ 2 , 2 ] [ 2 , 3 ] [ 2 m ]
b1, b
Row major matrix
[ n , 1 ] [ n , 2 ] [ n , 3 ] [ n , m ]
b1, u
u1, b
[ 1 , 1 ] [ 1 , 2 ] [ 1 , 3 ] [ 1 , 4 ]
[ 2 , 1 ] [ 2 , 2 ] [ 2 , 3 ] [ 2 , 4 ]
col 1 col 2 col 3 col 4
row 1 row 2
Column major matrix No of Columns = m = u2 – b2 + 1
A [i]
L 0
L 0 + (i-1)C
L 0 is the address of the first word allocated to the first element of vector A. C words are allocated for each element or node The address of Ai is given equation Loc (Ai) = L 0 + C (i-1) Let’s consider the more general case of representing a vector A whose lower bound for it’s subscript is given by some variable b. The location of Ai is then given by Loc (Ai) = L 0 + C (i-b)
Applications of Array
- Symbol Manipulation (matrix representation of polynomial equation)
- Sparse Matrix
Symbol Manipulation using Array
We can use array for different kind of operations in polynomial equation such as addition, subtraction, division, differentiation etc… We are interested in finding suitable representation for polynomial so that different operations like addition, subtraction etc… can be performed in efficient manner Array can be used to represent Polynomial equation
Matrix Representation of Polynomial equation Y Y^2 Y^3 Y^4 X X Y X Y^2 X Y^3 X Y^4 X^2 X^2 Y X^2 Y^2 X^2 Y^3 X^2 Y^4 X^3 X^3 Y X^3 Y^2 X^3 Y^3 X^3 Y^4 X^4 X^4 Y X^4 Y^2 X^4 Y^3 X^4 Y^4
e.g. 2x^2 +5xy+Y^2 is represented in matrix form as below
e.g. x^2 +3xy+Y^2 +Y-X is represented in matrix form as below Y Y^2 Y^3 Y^4 0 0 1 0 0 X 0 5 0 0 0 X^2 2 0 0 0 0 X^3 0 0 0 0 0 X^4 0 0 0 0 0
Y Y^2 Y^3 Y^4
X - 1 3 0 0 0
X^2 1 0 0 0 0
X^3 0 0 0 0 0
X^4 0 0 0 0 0
Once we have algorithm for converting the polynomial equation to an array representation and another algorithm for converting array to polynomial equation, then different operations in array (matrix) will be corresponding operations of polynomial equation
What is sparse matrix? Explain
An mXn matrix is said to be sparse if “many” of its elements are zero. A matrix that is not sparse is called a dense matrix. We can device a simple representation scheme whose space requirement equals the size of the non- zero elements.
Fig (c )
COLUMN A 1 3 6 ROW 2 5 9 1 1 3 1 2 2 3 4 4 7 3 7 5 5 8 4 8 6 7 4 5 0 7 1 10 6 9 8 3 12 9 4 3 10 7 5
Fig(d)
A more efficient representation in terms of storage requirement and access time to the row of the matrix is shown in fid (d). The row vector changed so that its ith^ element is the index to the first of the column indices for the element in row I of the matrix.
Linked Representation of Sparse matrix Typical node to represent non-zero element is
Row Number
Column Number
Value Pointer To Next Node
1 3 6 1 5 9 2 1 2 2 4 7
6 4 3 6 7 5 NULL
ROW NO (^) First Column for row no (^) COLUMN NO
Write algorithms for Stack Operations – PUSH, POP, PEEP
A linear list which allows insertion and deletion of an element at one end only is called stack. The insertion operation is called as PUSH and deletion operation as POP. The most and least accessible elements in stack are known as top and bottom of the stack respectively. Since insertion and deletion operations are performed at one end of a stack, the elements can only be removed in the opposite orders from that in which they were added to the stack; such a linear list is referred to as a LIFO (last in first out) list.
A pointer TOP keeps track of the top element in the stack. Initially, when the stack is empty, TOP has a value of “one” and so on. Each time a new element is inserted in the stack, the pointer is incremented by “one” before, the element is placed on the stack. The pointer is decremented by “one” each time a deletion is made from the stack.
Applications of Stack Recursion Keeping track of function calls Evaluation of expressions Reversing characters Servicing hardware interrupts Solving combinatorial problems using backtracking.
Procedure : PUSH (S, TOP, X) This procedure inserts an element x to the top of a stack which is represented by a vector S containing N elements with a pointer TOP denoting the top element in the stack.
Write an algorithm to change the ith^ value of stack to value X
PROCEDURE : CHANGE (S, TOP, X, I) This procedure changes the value of the Ith^ element from the top of the stack to the value containing in X. Stack is represented by a vector S containing N elements.
1. [Check for stack Underflow] If TOP – I + 1 ≤ 0 Then Write (‘STACK UNDERFLOW ON CHANGE’) Return 2. [Change Ith^ element from top of the stack] S[TOP – I + 1] ← X 3. [Finished] Return
Write an algorithm which will check that the given string belongs to following
grammar or not. L={wcwR^ | w Є {a,b}}(Where wR*^ is the reverse of w)
Algorithm : RECOGNIZE Given an input string named STRING on the alphabet {a, b, c} which contains a blank in its rightmost character position and function NEXTCHAR which returns the next symbol in STRING, this algorithm determines whether the contents of STRING belong to the above language. The vector S represents the stack, and TOP is a pointer to the top element of the stack.
1. [Initialize stack by placing a letter ‘c’ on the top] TOP ← 1 S [TOP] ← ‘c’ 2. [Get and stack symbols either ‘c’ or blank is encountered] NEXT ← NEXTCHAR (STRING) Repeat while NEXT ≠ ‘c’ If NEXT = ‘ ‘ Then Write (‘Invalid String’) Exit Else Call PUSH (S, TOP, NEXT) NEXT ← NEXTCHAR (STRING) 3. [Scan characters following ‘c’; Compare them to the characters on stack] Repeat While S [TOP] ≠ ‘c’ NEXT ← NEXTCHAR (STRING) X ← POP (S, TOP) If NEXT ≠ X Then Write (‘INVALID STRING’) Exit 4. [Next symbol must be blank] If NEXT ≠ ‘ ‘ Then Write (‘VALID STRING’) Else Write (‘INVALID STRING’) 5. [Finished] Exit
C program for GCD using recursion
Write an algorithm to find factorial of given no using recursion
Algorithm: FACTORIAL
Given integer N, this algorithm computes factorial of N. Stack A is used to store an activation record associated with each recursive call. Each activation record contains the current value of N and the current return address RET_ADDE. TEMP_REC is also a record which contains two variables PARAM & ADDRESS.TOP is a pointer to the top element of stack A. Initially return address is set to the main calling address. PARAM is set to initial value N.
#include<stdio.h> int Find_GCD(int, int);
void main() { int n1, n2, gcd; scanf(“%d %d”,&n1, &n2); gcd = Find_GCD(n1, &n2); printf(“GCD of %d and %d is %d”, n1, n2, gcd); }
int Find_GCD(int m, int n) { int gcdVal; if(n>m) { gcdVal = Find_GCD(n,m); } else if(n==0) { gcdVal = m; } else { gcdVal = Find_GCD(n, m%n); } return(gcdVal); }
Give difference between recursion and iteration
Iteration Recursion In iteration, a problem is converted into a train of steps that are finished one at a time, one after another
Recursion is like piling all of those steps on top of each other and then quashing them all into the solution. With iteration, each step clearly leads onto the next, like stepping stones across a river
In recursion, each step replicates itself at a smaller scale, so that all of them combined together eventually solve the problem. Any iterative problem is solved recursively Not all recursive problem can solved by iteration It does not use Stack It uses Stack
1. [Save N and return Address] CALL PUSH (A, TOP, TEMP_REC) 2. [Is the base criterion found?] If N= then FACTORIAL 1 GO TO Step 4 Else PARAM N- 1 ADDRESS Step 3 GO TO Step 1 3. [Calculate N!] FACTORIAL N * FACTORIAL 4. [Restore previous N and return address] TEMP_RECPOP(A,TOP) (i.e. PARAMN, ADDRESSRET_ADDR) GO TO ADDRESS
1. [Initialize stack] TOP 1 S[TOP] ‘(‘ 2. [Initialize output string and rank count ] POLISH ‘ ‘ RANK 0 3. [Get first input symbol] NEXTNEXTCHAR (INFIX) 4. [Translate the infix expression ] Repeat thru step 7 while NEXT != ‘ ‘ 5. [Remove symbols with greater precedence from stack] IF TOP < 1 Then write (‘INVALID’) EXIT Repeat while G (S[TOP]) > F(NEXT) TEMP POP (S, TOP) POLISH POLISH O TEMP RANK RANK + R(TEMP) IF RANK < Then write ‘INVALID’) EXIT 6. [Are there matching parentheses] IF G(S[TOP]) != F(NEXT) Then call PUSH (S,TOP, NEXT) Else POP (S,TOP) 7. [Get next symbol] NEXT NEXTCHAR(INFIX) 8. [Is the expression valid] IF TOP != 0 OR RANK != 1 Then write (‘INVALID ‘) Else write (‘VALID ’)
Trace the conversion of infix to postfix form in tabular form.
(i) ( A + B * C / D - E + F / G / ( H + I ) )
- ( Input Symbol Content of stack Reverse polish Rank - ( ( (
- A ( (
- B ( ( + B A
- C ( ( + * C A B
- D ( ( + / D A B C * - - ( ( - A B C * D / +
- E ( ( - E A B C * D / +
-
- F ( ( + F A B C * D / + E -
- / ( ( + / A B C * D / + E – F
- G ( ( + / G A B C * D / + E – F
- / ( ( + / A B C * D / + E – F G /
- ( ( ( + / ( A B C * D / + E – F G /
- H ( ( + / ( H A B C * D / + E – F G /
- ( ( + / ( + A B C * D / + E – F G / H
- I ( ( + / ( + I A B C * D / + E – F G / H
- ) ( ( + / A B C * D / + E – F G / H I +
- ) ( A B C * D / + E – F G / H I + / +
- ) A B C * D / + E – F G / H I + / +
