Data structure GRAPHS, Summaries of Data Structures and Algorithms

Download Data structure GRAPHS and more Summaries Data Structures and Algorithms in PDF only on Docsity!

GRAPHS

SUNITA. D. RATHOD

GRAPHS

A Graph is a non-linear data structure consisting of vertices and edges.

The vertices are sometimes also referred to as nodes and the edges are lines or arcs that connect any two nodes in the graph.

Definition

A Graph is composed of a set of vertices( V ) and a set of edges( E ). The graph is denoted by G(E, V).

GRAPH TERMINOLOGY

Path

A path can be defined as the sequence of nodes that are followed in order to reach some terminal node V from the initial node U.

Closed Path

A path will be called as closed path if the initial node is same as terminal node. A path will be closed path if V 0 =VN.

Simple Path

If all the nodes of the graph are distinct with an exception V 0 =VN, then such path P is called as closed simple path.

GRAPH TERMINOLOGY

Cycle

A cycle can be defined as the path which has no repeated edges or vertices except the first and last vertices.

Connected Graph

A connected graph is the one in which some path exists between every two vertices (u, v) in V. There are no isolated nodes in connected graph.

Complete Graph

A complete graph is the one in which every node is connected with all other nodes. A complete graph contain n(n-1)/2 edges where n is the number of nodes in the graph.

GRAPH TERMINOLOGY

Loop

An edge that is associated with the similar end points can be called as Loop.

Adjacent Nodes

If two nodes u and v are connected via an edge e, then the nodes u and v are called as neighbours or adjacent nodes.

Degree of the Node

A degree of a node is the number of edges that are connected with that node. A node with degree 0 is called as isolated node.

GRAPH REPRESENTATION

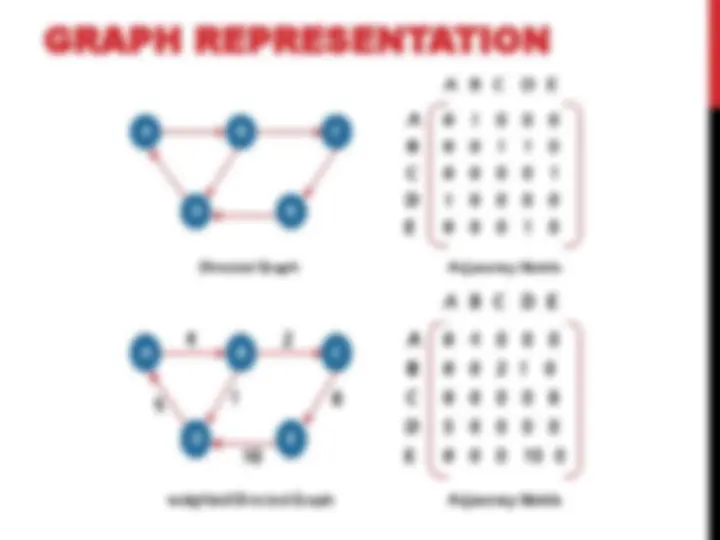
Graphs are commonly represented in two ways:

1. Adjacency Matrix
2. Adjacency List

GRAPH REPRESENTATION

GRAPH REPRESENTATION

2. Adjacency List

An adjacency list represents a graph as an array of linked lists.

The index of the array represents a vertex and each element in its linked list represents the other vertices that form an edge with the vertex.

GRAPH OPERATIONS

The most common graph operations are:

• Check if the element is present in the graph
• Graph Traversal
• Add elements(vertex, edges) to graph
• Finding the path from one vertex to another

BFS ALGORITHM

Step 1: SET STATUS = 1 (ready state) for each node in G

Step 2: Enqueue the starting node A and set its STATUS = 2 (waiting state)

Step 3: Repeat Steps 4 and 5 until QUEUE is empty

Step 4: Dequeue a node N. Process it and set its STATUS = 3 (processed state).

Step 5: Enqueue all the neighbours of N that are in the ready state (whose STATUS = 1) and set their STATUS = 2 (waiting state)

[END OF LOOP]

Step 6: EXIT

EXAMPLE

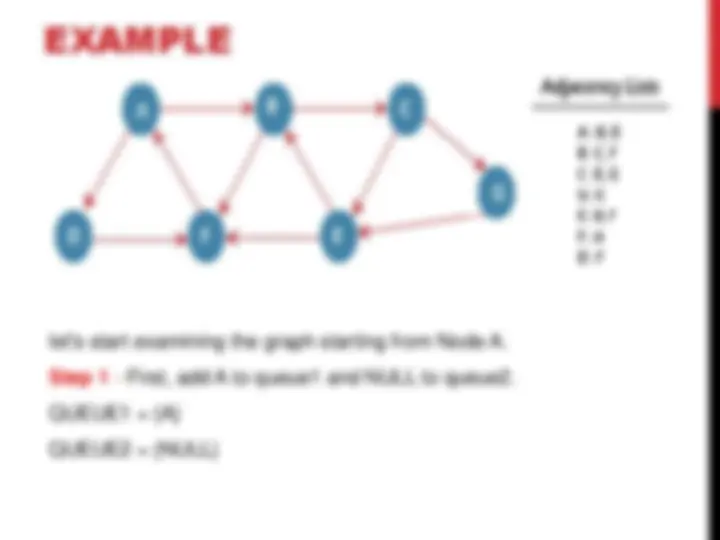
Step 2 - Now, delete node A from queue1 and add it into queue2. Insert all neighbors of node A to queue1.

QUEUE1 = {B, D}

QUEUE2 = {A}

Step 3 - Now, delete node B from queue1 and add it into queue2. Insert all neighbors of node B to queue1.

QUEUE1 = {D, C, F}

QUEUE2 = {A, B}

EXAMPLE

Step 4 - Now, delete node D from queue1 and add it into queue2. Insert all neighbors of node D to queue1. The only neighbor of Node D is F since it is already inserted, so it will not be inserted again.

QUEUE1 = {C, F}

QUEUE2 = {A, B, D}

Step 5 - Delete node C from queue1 and add it into queue2. Insert all neighbors of node C to queue1.

QUEUE1 = {F, E, G}

QUEUE2 = {A, B, D, C}

COMPLEXITY OF BFS ALGORITHM

Time complexity of BFS depends upon the data structure used to represent the graph. The time complexity of BFS algorithm is O(V+E) , since in the worst case, BFS algorithm explores every node and edge. In a graph, the number of vertices is O(V), whereas the number of edges is O(E).

The space complexity of BFS can be expressed as O(V) , where V is the number of vertices.

APPLICATIONS OF BFS

ALGORITHM

• BFS can be used to find the neighboring locations from a given source location.
• In a peer-to-peer network, BFS algorithm can be used as a traversal method to find all the neighboring nodes.
• BFS can be used in web crawlers to create web page indexes.
• BFS is used to determine the shortest path and minimum spanning tree.