Machine Learning Lecture 3: Concept Learning and Candidate Elimination Algorithm - Prof. G, Study notes of Computer Science

Download Machine Learning Lecture 3: Concept Learning and Candidate Elimination Algorithm - Prof. G and more Study notes Computer Science in PDF only on Docsity!

Intro. to machine learning (CSI 5325)

Lecture 3: concept learning

Greg Hamerly

Fall 2008

Some content from Tom Mitchell.

Outline

1 Concept learning

2 Candidate elimination algorithm (recap)

3 Picking new examples

4 The need for inductive bias

5 Where we are going

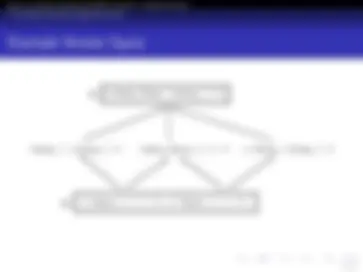
Candidate elimination algorithm (recap)

Example Version Space

S:

<Sunny, ?, ?, Strong, ?, ?> <Sunny, Warm, ?, ?, ?, ?>

{ <Sunny, Warm, ?, Strong, ?, ?> }

G: { <Sunny, ?, ?, ?, ?, ?>, ^ }

Candidate elimination algorithm (recap)

Representing Version Spaces

The General boundary, G, of version space VSH,D is the set of its maximally general members

The Specific boundary, S, of version space VSH,D is the set of its maximally specific members

Every member of the version space lies between these boundaries

VSH,D = {h ∈ H|(∃s ∈ S)(∃g ∈ G )(g ≥ h ≥ s)}

where x ≥ y means x is more general or equal to y

Candidate elimination algorithm (recap)

Candidate Elimination Algorithm – positive example

For a positive example d: Remove from G any hypothesis inconsistent with d

For each hypothesis s in S that is not consistent with d Remove s from S Add to S all minimal generalizations h of s such that h is consistent with d, and some member of G is more general than h Remove from S any hypothesis that is more general than another hypothesis in S

Candidate elimination algorithm (recap)

Candidate Elimination Algorithm – negative example

For a negative example d: Remove from S any hypothesis inconsistent with d

For each hypothesis g in G that is not consistent with d Remove g from G Add to G all minimal specializations h of g such that h is consistent with d, and some member of S is more specific than h Remove from G any hypothesis that is less general than another hypothesis in G

Candidate elimination algorithm (recap)

What about noisy data?

What would happen to the candidate elimination algorithm if it encountered an incorrectly-labeled example?

The algorithm removes every hypothesis that is inconsistent with some training example. Therefore, the true concept will be removed!

What does this show about our assumptions that the data has no noise? the hypothesis space contains the correct hypothesis?

Picking new examples

What ordering on the training examples?

Does the order of the training data matter? in correctness of the algorithm? in efficiency of the algorithm?

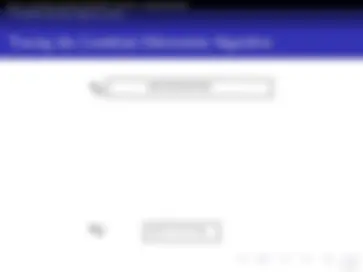
Picking new examples

How Should These Be Classified?

S:

<Sunny, ?, ?, Strong, ?, ?> <Sunny, Warm, ?, ?, ?, ?>

{ <Sunny, Warm, ?, Strong, ?, ?> }

G: { <Sunny, ?, ?, ?, ?, ?>, ^ }

〈Sunny Warm Normal Strong Cool Change〉 〈Rainy Cool Normal Light Warm Same〉 〈Sunny Warm Normal Light Warm Same〉

The need for inductive bias

What Justifies this Inductive Leap?

• 〈Sunny Warm Normal Strong Cool Change〉
• 〈Sunny Warm Normal Light Warm Same〉

S : 〈Sunny Warm Normal?? ?〉

Why believe we can classify the unseen

〈Sunny Warm Normal Strong Warm Same〉

The need for inductive bias

An UNbiased learner

Idea: Choose H that expresses every teachable concept (i.e., H is the power set of X ) Consider H′^ = disjunctions, conjunctions, negations over previous H. E.g.,

〈Sunny Warm Normal?? ?〉 ∨ ¬〈????? Change〉

What are S, G in this case? S ← G ←

The need for inductive bias

Inductive Bias

Consider concept learning algorithm L instances X , target concept c training examples Dc = {〈x, c(x)〉} let L(xi , Dc ) denote the classification assigned to the instance xi by L after training on data Dc.

Definition: The inductive bias of L is any minimal set of assertions B such that for any target concept c and corresponding training examples Dc

(∀xi ∈ X )[(B ∧ Dc ∧ xi ) ` L(xi , Dc )]

where A ` B means A logically entails B

The need for inductive bias

Three Learners with Different Biases

1 Rote learner: Store examples, Classify x iff it matches previously observed example. 2 Version space candidate elimination algorithm 3 Find-S

The need for inductive bias

Inductive bias and tic-tac-toe

What is the inductive bias of the TTT player you’re writing?