



























Study with the several resources on Docsity

Earn points by helping other students or get them with a premium plan


Prepare for your exams
Study with the several resources on Docsity

Earn points to download
Earn points by helping other students or get them with a premium plan
Community
Ask the community for help and clear up your study doubts
Discover the best universities in your country according to Docsity users
Free resources
Download our free guides on studying techniques, anxiety management strategies, and thesis advice from Docsity tutors
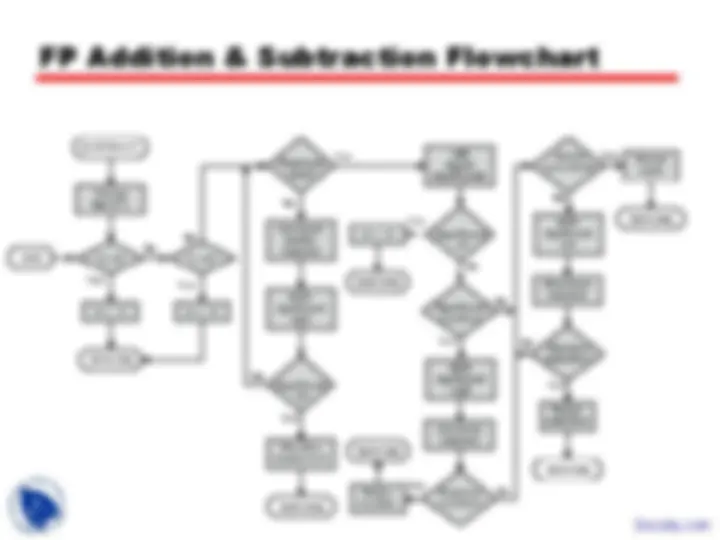
An in-depth exploration of computer arithmetic, focusing on the arithmetic & logic unit (alu), integer representation using sign-magnitude and two's complement, and floating point numbers. Learn how computers handle calculations, represent numbers, and perform arithmetic operations.
Typology: Slides
1 / 39

This page cannot be seen from the preview
Don't miss anything!
































Chapter 9
Computer Arithmetic
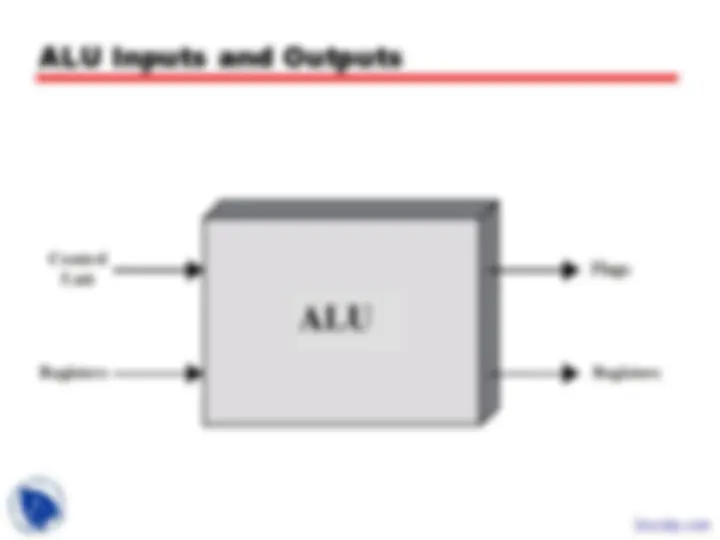
Arithmetic & Logic Unit
Integer Representation
Sign-Magnitude
Benefits
Negation Special Case 1
Range of Numbers
Conversion Between Lengths
Hardware for Addition and Subtraction
Multiplication
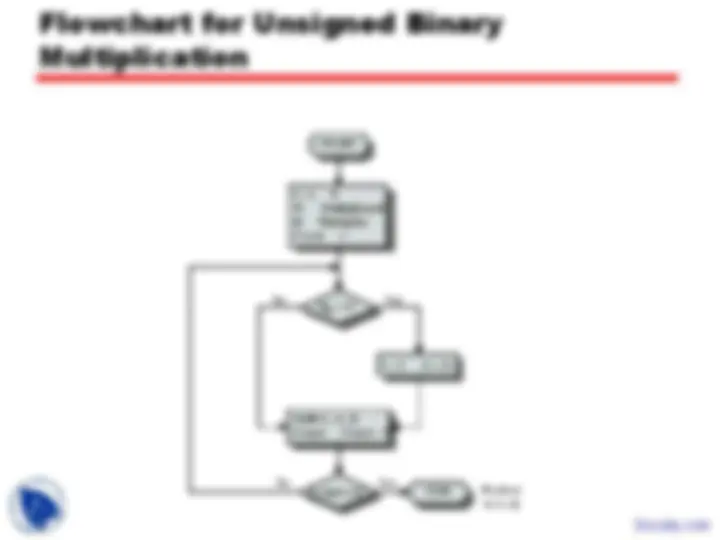
Unsigned Binary Multiplication
Execution of Example
Multiplying Negative Numbers
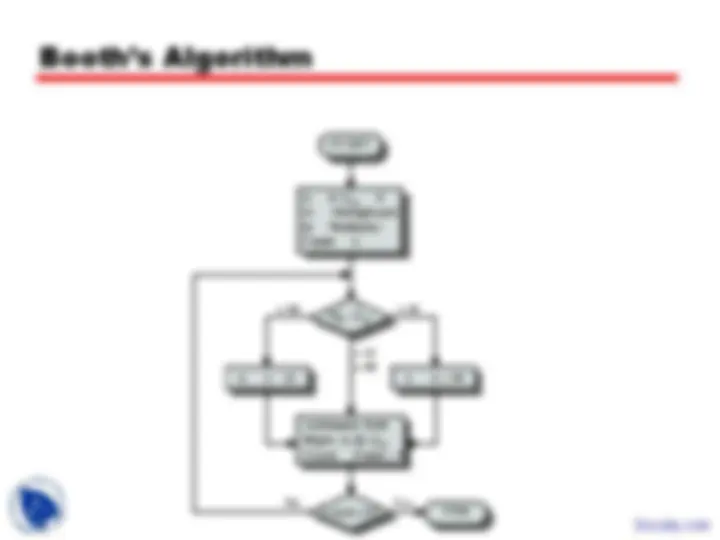
Booth’s Algorithm