Closure Properties - Automata and Complexity Theory - Lecture Slides, Slides of Theory of Automata

Download Closure Properties - Automata and Complexity Theory - Lecture Slides and more Slides Theory of Automata in PDF only on Docsity!

1

Closure Properties of Regular

Languages

Union, Intersection, Difference,Concatenation, Kleene Closure,

Reversal, Homomorphism, Inverse

Homomorphism

2

Closure Properties

Recall a closure property is a statement that a certain operation on languages,when applied to languages in a class(e.g., the regular languages), producesa result that is also in that class.

For regular languages, we can use any of its representations to prove a closureproperty.

4

Closure Under Concatenation

and Kleene Closure

Same idea:



RS is a regular expression whose languageis LM.



R* is a regular expression whose languageis L*.

5

Closure Under Intersection

If L and M are regular languages, then so is L

M.

Proof: Let A and B be DFA’s whose languages are L and M, respectively.

Construct C, the product automaton of A and B.

Make the final states of C be the pairs consisting of final states of both A and B.

7

Closure Under Difference

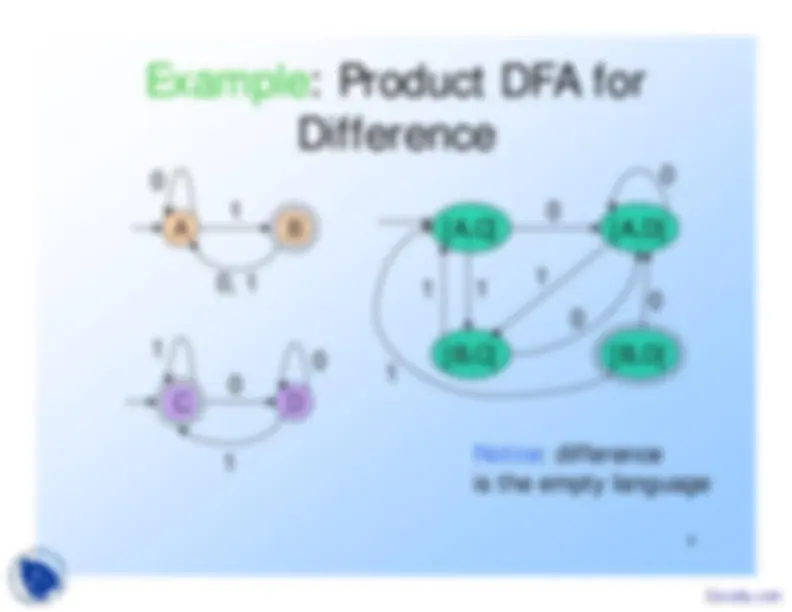
If L and M are regular languages, then so is

L – M

= strings in L but not M.

Proof: Let A and B be DFA’s whose languages are L and M, respectively.

Construct C, the product automaton of A and B.

Make the final states of C be the pairs where A-state is final but B-state is not.

8

Example: Product DFA for

Difference

A C

B D

0

1

0, 1

1

1

0

0

[A,C]

[A,D]

0

[B,C]

1

0

1

0

1

[B,D]

0

1

Notice: differenceis the empty language

10

Closure Under Reversal

Recall example of a DFA that accepted the binary strings that, as integers weredivisible by 23.

We said that the language of binary strings whose reversal was divisible by23 was also regular, but the DFAconstruction was very tricky.

Good application of reversal-closure.

11

Closure Under Reversal – (2)

Given language L, L

R

is the set of strings

whose reversal is in L.

Example: L = {0, 01, 100}; L

R

Proof: Let E be a regular expression for L.

We show how to reverse E, to provide a regular expression E

R

for L

R

13

Example: Reversal of a RE

Let E =

E

R

R

R

R

R

R

R

R

R

R

14

Homomorphisms

A

homomorphism

on an alphabet is a

function that gives a string for eachsymbol in that alphabet.

Example: h(0) = ab; h(1) =

ε

Extend to strings by h(a

1

…a

n

h(a

1

)…h(a

n

Example: h(01010) = ababab.

16

Example: Closure under

Homomorphism

Let h(0) = ab; h(1) =

ε

Let L be the language of regular expression

Then h(L) is the language of regular expression

ab

ε

ε

ab

Note: use parenthesesto enforce the propergrouping.

17

Example – Continued

ab

ε

ε

ab

)* can be simplified.

ε

ε

, so

ab

ε

ab

ε

ε

is the identity under concatenation.



That is,

ε

E = E

ε

= E for any RE

E.

Thus,

ab

ε

ε

ab

ab

ε

ε

ab

ab

ab

Finally, L(

ab

) is contained in L((

ab

so a RE for h(L) is (

ab

19

Example: Inverse Homomorphism

Let h(0) = ab; h(1) =

ε

Let L = {abab, baba}.

h

(L) = the language with two 0’s and

any number of 1’s = L(

Notice: no string maps tobaba; any string with exactlytwo 0’s maps to abab.

20

Closure Proof for Inverse

Homomorphism

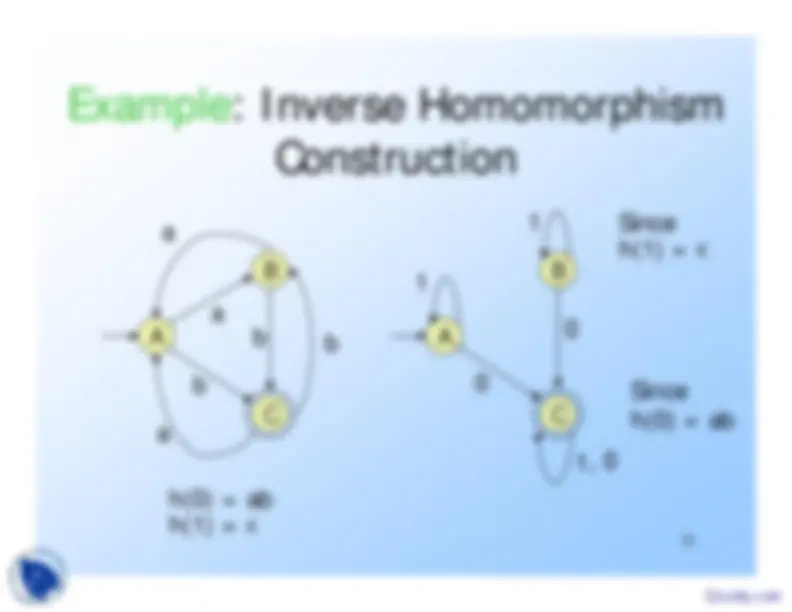
Start with a DFA A for L.

Construct a DFA B

for h

(L) with:



The same set of states.



The same start state.



The same final states.



Input alphabet = the symbols to whichhomomorphism h applies.