Download Bayesian Econometric Models - Econometric Analysis of Panel Data - Lecture Slides and more Slides Econometrics and Mathematical Economics in PDF only on Docsity!

Econometric Analysis of Panel Data

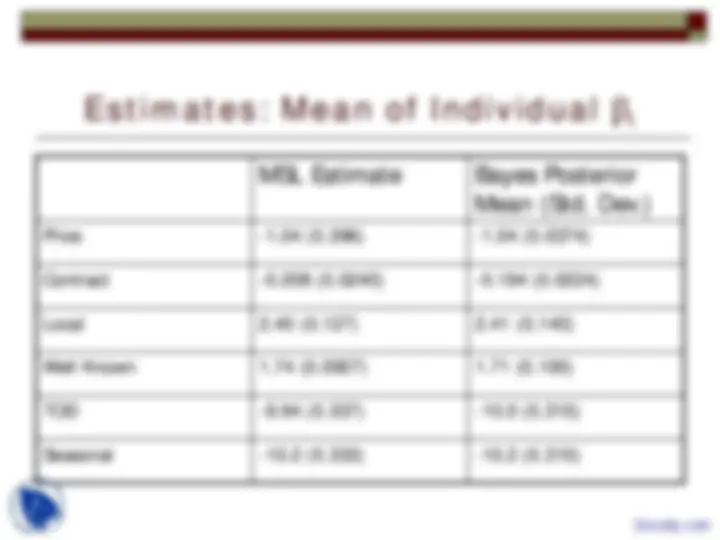
21. Bayesian Econometric Models

for Panel Data

A Philosophical Underpinning

 A method of using new information to update

existing beliefs about probabilities of events

 Bayes Theorem for events. (Conceived for

updating beliefs about games of chance)

Pr(A,B)

Pr(A | B)

Pr(B)

Pr(B | A)Pr(A)

Pr(B)

Paradigms

 Classical

 Formulate the theory

 Gather evidence

 Evidence consistent with theory? Theory stands and waits for

more evidence to be gathered

 Evidence conflicts with theory? Theory falls

 Bayesian

 Formulate the theory

 Assemble existing evidence on the theory

 Form beliefs based on existing evidence

 Gather evidence

 Combine beliefs with new evidence

 Revise beliefs regarding the theory

Applications of the Paradigm

 Classical econometricians doggedly cling to

their theories even when the evidence conflicts

with them – that is what specification searches

are all about.

 Bayesian econometricians NEVER incorporate

prior evidence in their estimators – priors are

always studiously noninformative. (Informative

priors taint the analysis.) As practiced,

Bayesian analysis is not Bayesian.

The Likelihood Principle

 The likelihood embodies ALL the

current information about the

parameters and the data

 Proportional likelihoods should lead to

the same inferences

Application:

 (1) 20 Bernoulli trials, 7 successes (Binomial)

 (2) N Bernoulli trials until the 7

th

success (Negative

Binomial)

7 13

L( ;N 20, s 7) (1 )

7 13

L( ;N 20, s 7) (1 )

The Bayesian Estimator

 The posterior distribution embodies all that is

“believed” about the model.

 Posterior = f(model|data)

= Likelihood(θ,data) * prior(θ) / P(data)

 “Estimation” amounts to examining the

characteristics of the posterior distribution(s).

 Mean, variance

 Distribution

 Intervals containing specified probabilities

Priors and Posteriors

 The Achilles heel of Bayesian Econometrics

 Noninformative and Informative priors for estimation of

parameters

 Noninformative (diffuse) priors: How to incorporate the total

lack of prior belief in the Bayesian estimator. The estimator

becomes solely a function of the likelihood

 Informative prior: Some prior information enters the

estimator. The estimator mixes the information in the

likelihood with the prior information.

 Improper and Proper priors

 P(θ) is uniform over the allowable range of θ

 Cannot integrate to 1.0 if the range is infinite.

 Salvation – improper, but noninformative priors will fall out of

the posterior.

Conjugate Prior

s N s s N s

a 1 b 1

Mathematical device to produce a tractable posterior

This is a typical application

N (^) (N 1) L( ;N,s)= (1 ) (1 )

s (s 1) (N s 1)

(a+b) Use a , p( )= (1 )

(a) (b)

Po

− −

− −

  Γ + θ (^)   θ − θ = θ − θ

  Γ^ +^ Γ^ −^ +

Γ θ θ − θ Γ Γ

conjugate beta prior

s N s a 1 b 1

1 s N s a 1 b 1

0

s a 1 N s b 1

1 s a 1 N s b

0

(N 2) (a+b) (1 ) (1 ) (s 1) (N s 1) (a) (b) sterior (N 2) (a+b) (1 ) (1 ) d (s 1) (N s 1) (a) (b)

(1 )

(1 )

− − −

− − −

• − − + −

• − − + −

 Γ +   Γ   θ^ − θ^   θ^ − θ   Γ^ +^ Γ^ −^ +^   Γ^ Γ  =  Γ +   Γ   θ^ − θ^   θ^ − θ^  θ  Γ^ +^ Γ^ −^ +^   Γ^ Γ 

θ − θ

θ − θ

1

a Beta distribution.

d

s+a Posterior mean = (we used a = b = 1 before)

N+a+b

=

θ

THE Question

Where does the prior come from?

Reconciliation

A Theorem (Bernstein-Von Mises)

 The posterior distribution converges to normal with

covariance matrix equal to 1/N times the information

matrix (same as classical MLE). (The distribution that is

converging is the posterior, not the sampling

distribution of the estimator of the posterior mean.)

 The posterior mean (empirical) converges to the mode

of the likelihood function. Same as the MLE. A proper

prior disappears asymptotically.

 Asymptotic sampling distribution of the posterior mean

is the same as that of the MLE.

Bayesian Estimators

 First generation: Do the integration (math)

 Contemporary - Simulation:

 (1) Deduce the posterior

 (2) Draw random samples of draws from the posterior and

compute the sample means and variances of the samples.

(Relies on the law of large numbers.)

= ∫

f(data | )p( ) E( | data) d β f(data)

β β β β β

Marginal Posterior for β

2

2 2 / 2 1 / 2

2 1 / 2 2

2 1

After integrating out of the joint posterior:

[ ] ( / 2) [2 ] | | ( 2) ( | , ). [ ( ) ( )]

n-K

Multivariate t with mean and variance matrix [ ( ) ]

2

The Bayesi

v K

d K

ds d K

d f

ds

s n K

σ

π

− −

−

Γ + ′

Γ + ∝

• − ′^ ′ −

− −

X X

β y X β b X X β b

b X'X

an 'estimator' equals the MLE. Of course; the prior was

noninformative. The only information available is in the likelihood.

Nonlinear Models and Simulation

 Bayesian inference over parameters in a

nonlinear model:

 1. Parameterize the model

 2. Form the likelihood conditioned on the

parameters

 3. Develop the priors – joint prior for all model

parameters

 4. Posterior is proportional to likelihood times prior.

(Usually requires conjugate priors to be tractable.)

 5. Draw observations from the posterior to study its

characteristics.