Basics of Counting - Discrete Mathematics - Lecture Slides, Slides of Discrete Mathematics

Download Basics of Counting - Discrete Mathematics - Lecture Slides and more Slides Discrete Mathematics in PDF only on Docsity!

1

Basics of Counting

2

The product rule

• Also called the multiplication rule

• If there are n 1 ways to do task 1, and n 2 ways to

do task 2

• Then there are n 1 n 2 ways to do both tasks in

sequence

• This applies when doing the “procedure” is made up

of separate tasks

• We must make one choice AND a second choice

4

Product rule example

More sample questions…

• How many strings of 4 decimal digits…

a) Do not contain the same digit twice?

We want to chose a digit, then another that is not the same,

then another…

• First digit: 10 possibilities
• Second digit: 9 possibilities (all but first digit)
• Third digit: 8 possibilities
• Fourth digit: 7 possibilities

Total = 1098*7 = 5040

b) End with an even digit?

First three digits have 10 possibilities

Last digit has 5 possibilities

Total = 101010*5 = 5000

5

The sum rule

• Also called the addition rule

• If there are n 1 ways to do task 1, and n 2 ways to

do task 2

• If these tasks can be done at the same time, then…
• Then there are n 1 + n 2 ways to do one of the two tasks
• We must make one choice OR a second choice

7

Sum rule example

More sample questions

• How many strings of 4 decimal digits…

• Have exactly three digits that are 9s?

• The string can have:
  • The non-9 as the first digit
  • OR the non-9 as the second digit
  • OR the non-9 as the third digit
  • OR the non-9 as the fourth digit
  • Thus, we use the sum rule
• For each of those cases, there are 9 possibilities for

the non-9 digit (any number other than 9)

• Thus, the answer is 9+9+9+9 = 36

8

More complex counting problems

• We combining the product rule and the

sum rule

• Thus we can solve more interesting and

complex problems

10

Wedding pictures example

• Consider a wedding picture of 6 people
  • There are 10 people, including the bride and groom

b) How many possibilities are there if the bride and

groom must both be in the picture

Product rule: place the bride/groom AND then place the rest of

the party

First place the bride and groom

• She can be in one of 6 positions
• He can be in one 5 remaining positions
• Total of 30 possibilities

Next, place the other four people via the product rule

• There are 8 people to choose for the third person, 7 for the fourth, etc.
• Total = 876*5 = 1680

Product rule yields 30 * 1680 = 50,400 possibilities Docsity.com

11

Wedding pictures example

• Consider a wedding picture of 6 people
  • There are 10 people, including the bride and groom

c) How many possibilities are there if only one of the bride and

groom are in the picture

Sum rule: place only the bride

• Product rule: place the bride AND then place the rest of the party
• First place the bride  She can be in one of 6 positions
• Next, place the other five people via the product rule There are 8 people to choose for the second person, 7 for the third, etc. » We can’t choose the groom! Total = 87654 = 6720
• Product rule yields 6 * 6720 = 40,320 possibilities  OR place only the groom
• Same possibilities as for bride: 40, Sum rule yields 40,320 + 40,320 = 80,640 possibilities

13

The inclusion-exclusion principle

• When counting the possibilities, we can’t

include a given outcome more than once!

• |A 1 U A 2 | = |A 1 | + |A 2 | - |A 1 ∩ A 2 |
  • Let A 1 have 5 elements, A 2 have 3 elements,

and 1 element be both in A 1 and A 2

• Total in the union is 5+3-1 = 7, not 8

14

Inclusion-exclusion example

• How may bit strings of length eight start with 1 or end with 00?
• Count bit strings that start with 1
  • Rest of bits can be anything: 2^7 = 128
  • This is |A 1 |
• Count bit strings that end with 00
  • Rest of bits can be anything: 2^6 = 64
  • This is |A 2 |
• Count bit strings that both start with 1 and end with 00
  • Rest of the bits can be anything: 2^5 = 32
  • This is |A 1 ∩ A2 |
• Use formula |A 1 U A 2 | = |A 1 | + |A 2 | - |A 1 ∩ A 2 |
• Total is 128 + 64 – 32 = 160

16

Bit string possibilities

• Consider 5 consecutive 0s first
• Sum rule: the 5 consecutive 0’s can start at position 1, 2, 3, 4, 5, or 6
  • Starting at position 1
    • Remaining 5 bits can be anything: 2 5 = 32
  • Starting at position 2
    • First bit must be a 1
      • Otherwise, we are including possibilities from the previous case!
    • Remaining bits can be anything: 2 4 = 16
  • Starting at position 3
    • Second bit must be a 1 (same reason as above)
    • First bit and last 3 bits can be anything: 2^4 = 16
  • Starting at positions 4 and 5 and 6
    • Same as starting at positions 2 or 3: 16 each
  • Total = 32 + 16 + 16 + 16 + 16 + 16 = 112
• The 5 consecutive 1’s follow the same pattern, and have 112 possibilities
• There are two cases counted twice (that we thus need to exclude):

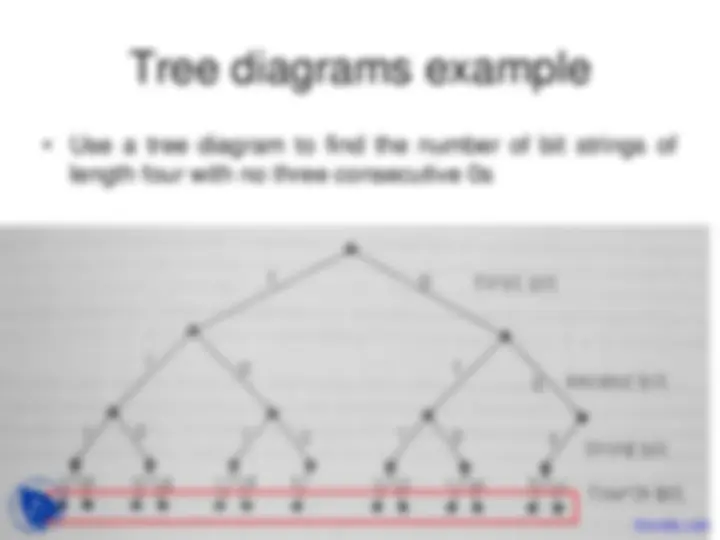
0000011111 and 1111100000

• Total = 112 + 112 – 2 = 222 Docsity.com

17

Tree diagrams

• We can use tree diagrams to enumerate

the possible choices

• Once the tree is laid out, the result is the

number of (valid) leaves

19

An example closer to home…

• How many ways can the Cavs finish the

season 9 and 2?

– This was from fall ’04….

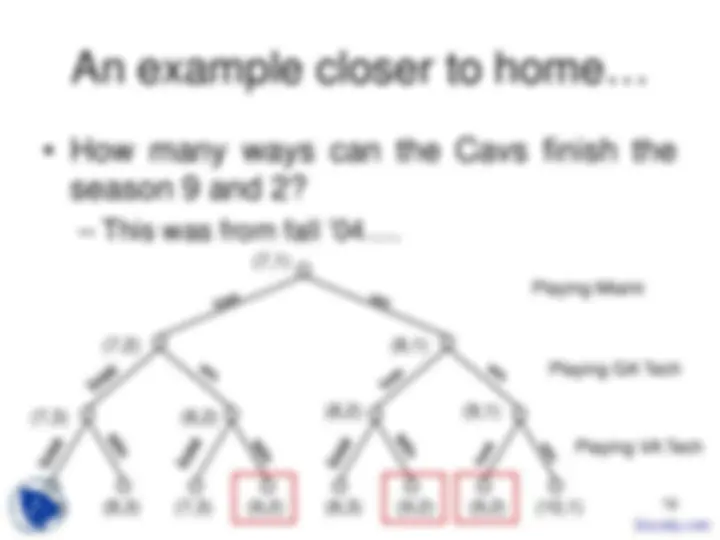
Playing Miami

Playing GA Tech

Playing VA Tech