Automata - Automata and Complexity Theory - Lecture Slides, Slides of Theory of Automata

Download Automata - Automata and Complexity Theory - Lecture Slides and more Slides Theory of Automata in PDF only on Docsity!

Automata theory

and formal languages

What is automata theory

• Automata theory is the study of abstract

computational devices

• Abstract devices are (simplified) models of

real computations

• Computations happen everywhere: On your

laptop, on your cell phone, in nature, …

• Why do we need abstract models?

A simple “computer”

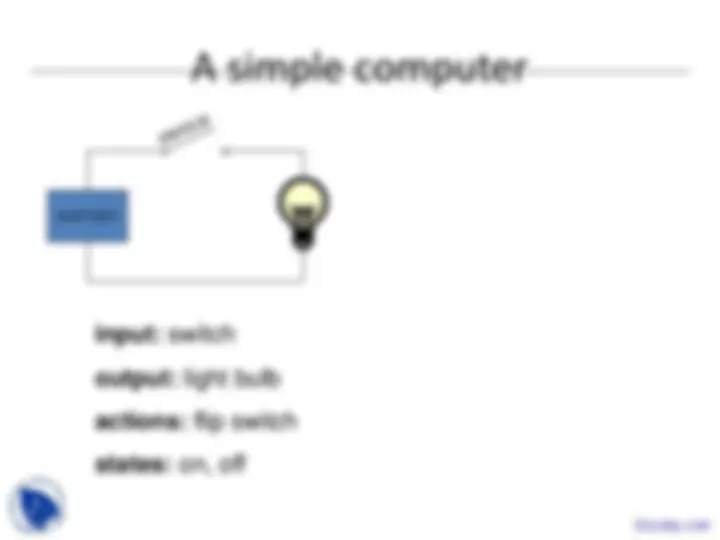
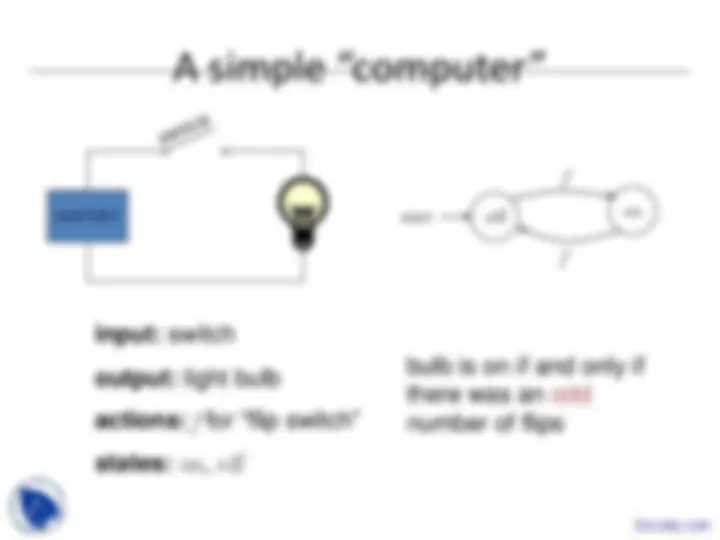
BATTERY (^) start off on

f

f

input: switch

output: light bulb actions: f for “flip switch” states: on, off

bulb is on if and only if there was an odd number of flips

Another “computer”

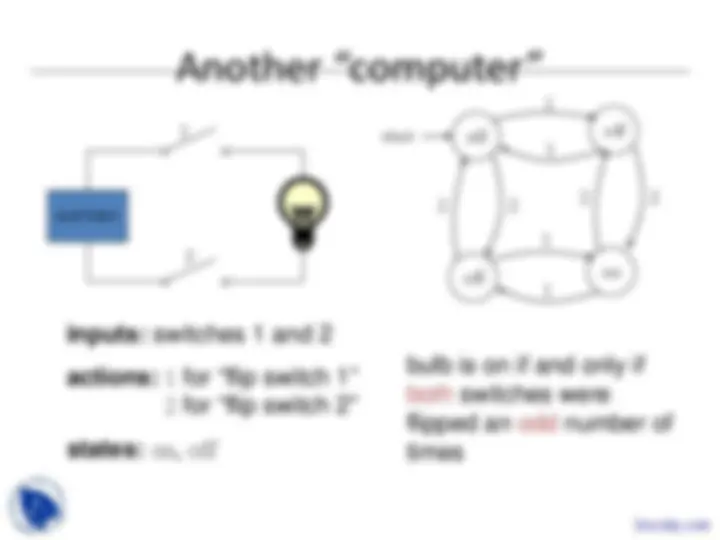
BATTERY

start off off

1

inputs: switches 1 and 2 actions: 1 for “flip switch 1” actions: 2 for “flip switch 2”

states: on, off

bulb is on if and only if both switches were flipped an odd number of times

1

2

1

off on

1

1

2 2 2 2

A design problem

• Such devices are difficult to reason about,

because they can be designed in an infinite

number of ways

• By representing them as abstract

computational devices, or automata, we will

learn how to answer such questions

These devices can model many things

• They can describe the operation of any “small computer”, like the control component of an alarm clock or a microwave
• They are also used in lexical analyzers to recognize well formed expressions in programming languages:

ab1 is a legal name of a variable in C 5u= is not

Some devices we will see

finite automata Devices with a finite amount of memory. Used to model “small” computers.

push-down automata

Devices with infinite memory that can be accessed in a restricted way. Used to model parsers, etc.

Turing Machines Devices with infinite memory.

Used to model any computer.

time-bounded Turing Machines

Infinite memory, but bounded running time. Used to model any computer program that runs in a “reasonable” amount of time. Docsity.com

Some highlights of the course

• Finite automata
  • We will understand what kinds of things a device with

finite memory can do, and what it cannot do

• Introduce simulation: the ability of one device to

“imitate” another device

• Introduce nondeterminism: the ability of a device to

make arbitrary choices

• Push-down automata
  • These devices are related to grammars, which

describe the structure of programming (and natural)

languages

Some highlights of the course

• Time-bounded Turing Machines
  • Many problems are possible to solve on a

computer in principle, but take too much time in

practice

• Traveling salesman: Given a list of cities, find the

shortest way to visit them and come back home

Hong Kong

Beijing

Shanghai

Xian Guangzhou

Chengdu

Preliminaries of automata theory

• How do we formalize the question
• First, we need a formal way of describing the

problems that we are interested in solving

Can device A solve problem B?

Alphabets and strings

• A common way to talk about words, number,

pairs of words, etc. is by representing them as

strings

• To define strings, we start with an alphabet
• Examples

An alphabet is a finite set of symbols.

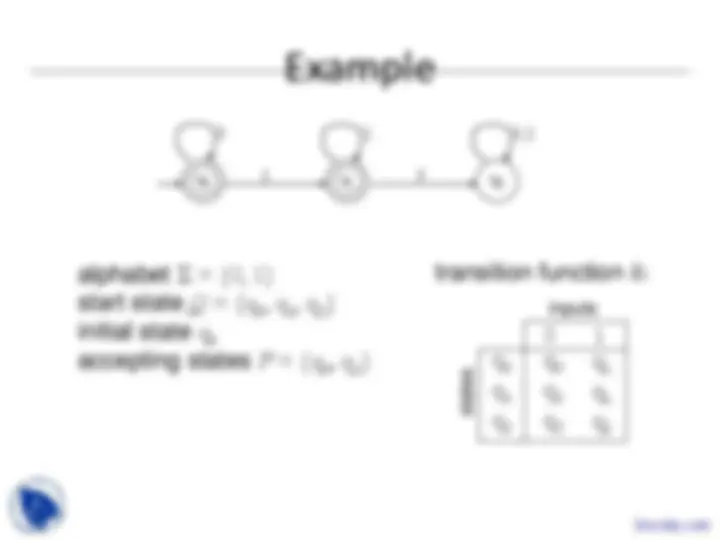
Σ 1 = {a, b, c, d, …, z}: the set of letters in English Σ 2 = {0, 1, …, 9}: the set of (base 10) digits Σ 3 = {a, b, …, z, #}: the set of letters plus the special symbol # Σ 4 = {(, )}: the set of open and closed brackets

Strings

• The empty string will be denoted by ε
• Examples

A string over alphabet Σ is a finite sequence

of symbols in Σ.

abfbz is a string over Σ 1 = {a, b, c, d, …, z} 9021 is a string over Σ 2 = {0, 1, …, 9} ab#bc is a string over Σ 3 = {a, b, …, z, #} ))()(() is a string over Σ 4 = {(, )}

Finite Automata

Example of a finite automaton

• There are states off and on, the automaton

starts in off and tries to reach the “good state”

on

• What sequences of f s lead to the good state?
• Answer: { f , fff , fffff , …} = { f n : n is odd}
• This is an example of a deterministic finite

automaton over alphabet { f }

off on

f

f